Вероятность суммы событий

Согласно аксиомам Колмогорова вероятность суммы двух несовместных событий равна сумме их вероятностей:

(10)

Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения:

(11)

Пример 10. Опыт: бросание двух игральных кубиков. Какова вероятность появления хотя бы одной шестерки?

Решение. События: - появление шестерки при бросании первого кубика, - появление шестерки при бросании второго кубика. Тогда - появление хотя бы одной шестерки при бросании двух кубиков, - появление непременно двух шестерок при бросании двух кубиков. По формуле (11) имеем

Эту задачу можно решить по-другому. Перейдем к противоположному событию:

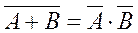
Отсюда

Следовательно,

Пример 11. Два игрока и попеременно бросают игральный кубик. Выигрывает тот, у которого раньше выпадет шестерка. Начинает игру . Какой игрок в более выгодном положении: или ?

Решение. Обозначим через 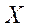выпадение шестерки, а через выпадение любого другого числа очков, т.е. числа очков от 1 до 5. К выигрышу (событие ) приводят следующие ситуации:

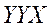или или и т.д.

Таким образом,

Вероятности этих событий равны

и т.д.

Следовательно, по теореме сложения несовместных событий

Итак, игрок , начавший игру, имеет некоторое, хотя и небольшое, преимущество

Формула полной вероятности

Пусть события образуют полную группу. Напомним, что при этом

В дальнейшем эти события будем называть гипотезами.

Пусть в результате опыта происходит некоторое событие и гипотезы образуют полную группу. Тогда имеет место формула полной вероятности:

(12)

или

Действительно, так как

,

то

По теореме сложения несовместных событий

Затем по теореме умножения зависимых событий

Пример 12. В механосборочный цех поступает деталей из цеха №1 и деталей из цеха №2. В цехе №1 производятся стандартных деталей, в цехе №2 - . Найти вероятность того, что наудачу взятая сборщиком деталь окажется стандартной

Решение. Случайный выбор детали можно условно произвести в два этапа: выбор цеха, а затем взятие детали.

- деталь изготовлена в цехе №1

- деталь изготовлена в цехе №2

- случайно выбранная деталь стандартна

События и образуют полную группу, при этом по условию задачи

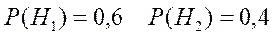
Далее: означает вероятность выбора стандартной детали при условии, что она была изготовлена в цехе №1, - вероятность выбора стандартной детали при условии, что она была изготовлена в цехе №2. По условию задачи

Тогда по формуле полной вероятности (12) имеем

Формула Байеса

Если опыт произведен, то с помощью формулы полной вероятности можно переоценить вероятности гипотез. Вероятности гипотез до опыта называют априорными, а после опыта – апостериорными.

Пусть события образуют полную группу. Тогда условная вероятность события при условии, что событие уже произошло, вычисляется по формуле

, (13)

где

Формула (13) называется формулой Байеса или формулой переоценки гипотез.

Для доказательства формулы (13) воспользуемся теоремой умножения зависимых событий. А именно,

Левые части равны, значит, равны и правые части этих равенств:

Отсюда немедленно получаем формулу (13)

Пример 13. В механосборочный цех поступает деталей из цеха №1 и деталей из цеха №2. В цехе №1 производятся стандартных деталей, в цехе №2 - . Найти вероятность того, что наудачу взятая сборщиком стандартная деталь была изготовлена в цехе №1

Решение. Условия этого примера полностью совпадают с условиями предыдущего примера. Воспользуемся тем, что вероятность выбора стандартной детали была уже вычислена, а именно, . Далее по формуле Байеса найдем вероятность того, что взятая наудачу стандартная деталь была изготовлена в цехе №1:

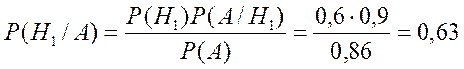
Схема Бернулли

Пусть производятся несколько независимых опытов, т.е. таких, что их исходы представляют собой независимые в совокупности события. Будем считать, что вероятность наступления некоторого события в каждом испытании не зависит от исходов других испытаний. В этом случае на практике часто используется так называемая схема Бернулли или схема независимых испытаний.

Предположим, что производится независимых опытов, в каждом из которых событие может произойти с вероятностью или не произойти с вероятностью . В каждом таком опыте ПЭС состоит только из двух элементарных событий:

где - событие произошло (успех), - событие не произошло (неудача). Очевидно, что множество всех элементарных исходов в независимых опытах равно . Например, при , т.е. когда опыт повторяется 3 раза, множество всех элементарных исходов равно . Действительно,

где

Найдем вероятности каждого элементарного события:

По определению сумма вероятностей всех элементарных исходов равна 1, т.е.

или

Формула Бернулли

Рассмотрим простейшую задачу, соответствующую схеме Бернулли: найти вероятность того, что в независимых испытаниях событие наступит раз .

Если производится независимых испытаний, в каждом из которых вероятность появления события равна , а вероятность его непоявления равна , то вероятность того, что событие наступит раз, определяется по формуле Бернулли:

(14)

Заметим, что вероятности являются коэффициентами в разложении бинома по известной формуле Ньютона:

Функцию называют производящей функцией, а совокупность всех таких вероятностей называют биномиальным распределением вероятностей.

Пример 14. Производится 3 выстрела по мишени. Вероятность попадания при одном выстреле равна . Найти вероятности промаха, одного, двух, трех попаданий.

Решение. В данной задаче требуется найти распределение вероятностей, исходя из заданных условий. Имеем

По формуле Бернулли получаем

Контроль:

Полученные результаты изобразим графически

Рис.3

Ломаная, соединяющая точки , называется многоугольником распределения вероятностей

Пример 15. Производится 3 выстрела по мишени. Вероятность попадания при первом выстреле равна , при втором - , при третьем - . Найти вероятности промаха, одного, двух, трех попаданий.