Положение материальной точки в пространстве можно задать тремя декартовыми координатами. Но это можно сделать и иначе, например, вместо декартовых взять полярные или какие-либо другие координаты. Существенно, однако, что при любом выборе число независимых координат, требующихся для однозначного определения положения материальной точки, которая может перемещаться в пространстве, как угодно, равно трем. Число независимых координат, с помощью которых определяется положение материальной точки, называется числом степеней свободы. Положение материальной точки задается тремя степенями свободы.
Если на движение материальной точки налагаются какие-либо ограничения, то число степеней свободы уменьшается. Например, в случае математического маятника точка может перемещаться только по поверхности сферы с центром в точке закрепления. Можно привести и много других примеров, в которых точка вынуждена находиться на какой-либо заданной поверхности. В подобных случаях говорят, что на тело наложены связи. Координаты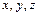 
такой точки должны удовлетворять соотношению вида 
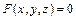, которое является уравнением рассматриваемой поверхности. Ввиду этого независимыми остаются только две координаты, например 
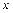и 
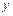. Третья координата может быть вычислена из уравнения связи 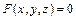. В этом случае материальная точка обладает двумя степенями свободы.
Если материальная точка перемещается вдоль какой-либо заданной кривой, то число независимых координат, требующихся для определения ее положения, снижается до одного. За координату можно принять например, расстояние от движущейся материальной точки до какой-либо точки рассматриваемой кривой, отсчитанное вдоль этой кривой. В таких случаях говорят, что материальная точка обладает одной степенью свободы.
|
|
Все сказанное без труда обобщается на произвольное число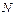 
материальных точек. Если эти точки перемещаются без всяких ограничений, то для определения их мгновенного положения надо задать 
координат. В этом случае система обладает степенями свободы. В некоторых задачах, однако, свобода перемещения материальных точек ограничена. На координат налагаются дополнительные условия, называемые связями. Для однозначного определения положения всех материальных точек системы достаточно знать меньшее число координат, обозначим его 
. Остальные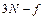 
координат могут быть вычислены из уравнений связи.
Необязательно в качестве независимых координат брать декартовы координаты. Для этой цели могут быть использованы любые величин 
, заданием которых положение материальных точек системы определяется однозначно. Такие величины называются обобщенными координатами. Движение системы определяется полностью, если обобщенные координаты будут найдены как функции времени. Производные обобщенных координат по времени называются обобщенными скоростями. Так при вращении материальной точки по окружности ее положение можно задать значением угла, который радиус-вектор вращающейся точки образует с положением его в некоторый определенный момент времени (например, в момент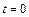 
), обобщенная скорость в этом случае имеет смысл угловой скорости вращающейся точки.
Обобщенные координаты могут быть выбраны любым способом, лишь бы они в любой момент времени полностью определяли положение механической системы. Однако, число независимых обобщеннных координат во всех случаях будет одно и то же. Оно называется числом степеней свободы системы.
|
|