Интеграл Римана был введен для ограниченных на отрезке функций. Естественно распространить понятие интеграла на случай бесконечного промежутка, а также на случай, когда подынтегральная функция является неограниченной.
Опр. Пусть 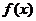 задана на луче
задана на луче  и интегрируема на любом конечном отрезке
и интегрируема на любом конечном отрезке 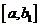 . Если существует предел
. Если существует предел 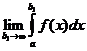 , то он называется несобственным интегралом первого рода и обозначается
, то он называется несобственным интегралом первого рода и обозначается 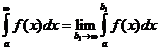 .
.
Опр. Пусть 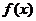 задана на полуинтервале
задана на полуинтервале 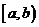 , интегрируема на любом конечном отрезке
, интегрируема на любом конечном отрезке 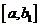 ,
,  и неограниченна в окрестности точки
и неограниченна в окрестности точки  . Если существует предел
. Если существует предел  , то он называется несобственным интегралом второго рода и обозначается
, то он называется несобственным интегралом второго рода и обозначается  .
.
Если указанные пределы конечные, то интегралы называются сходящимися, если бесконечные, то расходящимися, если пределы не существуют, то, говорят, что несобственные интегралы не существуют.
Замечание. Определение несобственного интеграла на полуинтервале 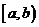 является содержательным лишь при неограниченности функции
является содержательным лишь при неограниченности функции 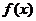 в окрестности точки
в окрестности точки  . Действительно, если
. Действительно, если 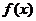 определена и ограничена на
определена и ограничена на 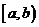 , то доопределив
, то доопределив 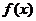 в точке
в точке  , получим интегрируемую на
, получим интегрируемую на  функцию. При этом интеграл не зависит от значения функции в одной точке
функцию. При этом интеграл не зависит от значения функции в одной точке  .
.
Теор. (Критерий Коши сходимости несобственных интегралов) Пусть задан интеграл 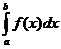 с единственной особенностью в точке
с единственной особенностью в точке  (
(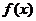 неограниченна в точке
неограниченна в точке  или
или 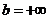 ). Для его сходимости необходимо и достаточно выполнения условия Коши:
). Для его сходимости необходимо и достаточно выполнения условия Коши:  .
.
Док. Рассмотрим функцию 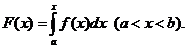 Тогда сходимость интеграла
Тогда сходимость интеграла 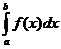 означает существование конечного предела функции
означает существование конечного предела функции  при
при  , а этот конечный предел, согласно Критерию Коши для функции
, а этот конечный предел, согласно Критерию Коши для функции  , существует в том и только том случае, когда
, существует в том и только том случае, когда  удовлетворяет условию:
удовлетворяет условию:  . Но
. Но  . Теорема доказана.
. Теорема доказана.
Свойства несобственных интегралов.
1. 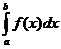 и
и 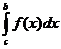
 , особенность в точке
, особенность в точке  - сходятся и расходятся одновременно. (Критерий Коши формулируется одинаково).
- сходятся и расходятся одновременно. (Критерий Коши формулируется одинаково).
2.  =
= 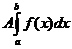 +
+ 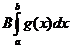 .
.
(Является следствием равенства 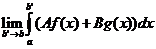 =
= 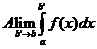 +
+  ).
).
3. Если  - сходится, то сходится
- сходится, то сходится 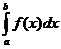 , причем
, причем  .
.
(Из условия Коши сходимости интеграла  следует условие Коши для интеграла
следует условие Коши для интеграла 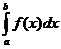 , т.к. справедливо неравенство
, т.к. справедливо неравенство 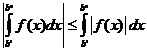 . Воспользуемся неравенством
. Воспользуемся неравенством 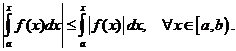 В силу сходимости интегралов существуют пределы от левой и правой частей. Переходя к пределам, получаем неравенство
В силу сходимости интегралов существуют пределы от левой и правой частей. Переходя к пределам, получаем неравенство  .)
.)
Несобственные интегралы от неотрицательных функций.
Теор. Если  , то для сходимости
, то для сходимости 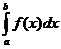 необходимо и достаточно, чтобы функция
необходимо и достаточно, чтобы функция 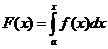 бала ограничена сверху, т.е.
бала ограничена сверху, т.е. 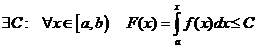 .
.
Док. Так как  возрастающая функция, то из сходимости интеграла следует
возрастающая функция, то из сходимости интеграла следует 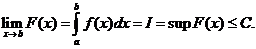 Обратно, если
Обратно, если  возрастающая функция и ограничена сверху, то она имеет конечный предел. Теорема доказана.
возрастающая функция и ограничена сверху, то она имеет конечный предел. Теорема доказана.
Теор. (Признак сравнения). Если  выполняется условие
выполняется условие  , тогда:
, тогда:
а). Из сходимости  следует сходимость
следует сходимость 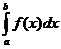 ;
;
б). Из расходимости 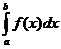 следует расходимость
следует расходимость  .
.
Док. а). Имеем 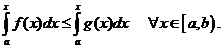 Так как
Так как 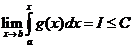 , то по предыдущей теореме
, то по предыдущей теореме 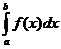 сходится.
сходится.
б). Из расходимости 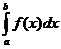 следует расходимость
следует расходимость  . Предположим обратное, что
. Предположим обратное, что  сходится, тогда по пункту а)
сходится, тогда по пункту а) 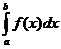 тоже сходится. Противоречие. Теорема доказана.
тоже сходится. Противоречие. Теорема доказана.
Теор. (Предельный признак сравнения). Пусть функции 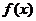 и
и  положительны и
положительны и 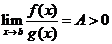 , тогда несобственные интегралы
, тогда несобственные интегралы 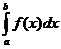 и
и  сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
Док. 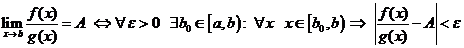 . Раскрывая последнее неравенство
. Раскрывая последнее неравенство 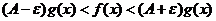 и используя признак сравнения, получим, что интегралы
и используя признак сравнения, получим, что интегралы 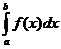 и
и  сходятся и расходятся одновременно. Теорема доказана.
сходятся и расходятся одновременно. Теорема доказана.
Интегрирование по частям несобственных интегралов.
Пример. Показать, что  сходится.
сходится.
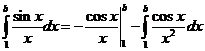 . Переходим к пределу
. Переходим к пределу  . Последний интеграл сходится абсолютно, т.к. сходится интеграл от модуля функции
. Последний интеграл сходится абсолютно, т.к. сходится интеграл от модуля функции 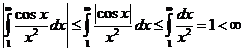 .
.
Аналогично показывают, что  тоже сходится.
тоже сходится.
Пример. Показать, что  сходится не абсолютно (условно).
сходится не абсолютно (условно).
 . Первый из последних двух интегралов расходится, второй – сходится, значит, их разность расходится.
. Первый из последних двух интегралов расходится, второй – сходится, значит, их разность расходится. 