Опр. Точкой 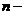 мерного пространства называется упорядоченная совокупность
мерного пространства называется упорядоченная совокупность  вещественных чисел
вещественных чисел  . Число
. Число  называется
называется 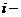 той координатой точки
той координатой точки  .
.
Опр. Пространством 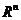 называется совокупность точек
называется совокупность точек 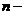 мерного пространства, расстояние между которыми определяется равенством
мерного пространства, расстояние между которыми определяется равенством 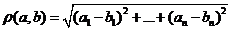 .
.
Расстояние обладает свойствами:
1.  ;
;
2.  ;
;
3.  .
.
Опр. 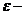 окрестностью точки
окрестностью точки  называется совокупность точек
называется совокупность точек  , удовлетворяющих неравенству
, удовлетворяющих неравенству 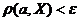 . Обозначается
. Обозначается  .
.
Опр. Прямоугольной окрестностью точки  называется совокупность точек
называется совокупность точек  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 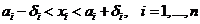 .
.  .
.
Утверждение. Какова бы ни была 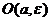 , существует
, существует  , такая, что
, такая, что 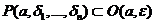 , и, наоборот, какова бы ни была
, и, наоборот, какова бы ни была  , существует
, существует 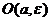 , такая, что
, такая, что 
 .
.
Опр. Говорят, что на множестве 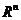 задана последовательность
задана последовательность 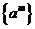 , если каждому натуральному
, если каждому натуральному 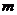 поставлена в соответствие точка
поставлена в соответствие точка  .(Не обязательно разные точки для разных
.(Не обязательно разные точки для разных 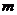 ).
).
Опр. Точка 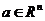 называется пределом последовательности
называется пределом последовательности 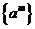 , если
, если 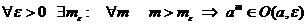 .
.
Утверждение. Для того чтобы 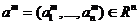 сходилась к точке
сходилась к точке  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы  .
.
Открытое множество.
Пусть 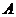 - некоторое множество точек в пространстве
- некоторое множество точек в пространстве 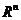 .
.
Опр. Точка 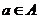 называется внутренней точкой, если существует
называется внутренней точкой, если существует 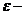 окрестность точки
окрестность точки  , содержащаяся в множестве
, содержащаяся в множестве 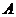 .
.
Опр. Множество называется открытым, если все его точки внутренние.
Опр. Точка  называется граничной точкой множества, если в любой
называется граничной точкой множества, если в любой 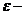 окрестности этой точки существуют точки, как принадлежащие множеству, так и не принадлежащие множеству.
окрестности этой точки существуют точки, как принадлежащие множеству, так и не принадлежащие множеству.
Опр. Множество 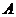 называется ограниченным, если существует
называется ограниченным, если существует 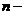 мерный шар с центром в начале координат, такой, что
мерный шар с центром в начале координат, такой, что  .
.
Опр. Множество называется связным, если любые две его точки можно соединить непрерывной прямой, принадлежащей этому множеству.
Опр. Областью называется открытое связное множество.
Предел и непрерывность функции.
Говорят, что на множестве  задана функция
задана функция  , если каждой точке
, если каждой точке 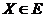 поставлено в соответствие действительное число
поставлено в соответствие действительное число 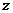 .
.
Опр. 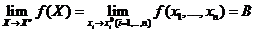 , если
, если 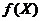 определена в некоторой окрестности точки
определена в некоторой окрестности точки 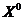 , за исключением быть может самой этой точки, и если
, за исключением быть может самой этой точки, и если  .
.
Опр. (По Гейне) 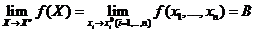 , если
, если 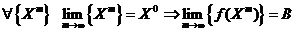 .
.
Опр. Функция  непрерывна в точке
непрерывна в точке 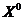 , если она определена в некоторой окрестности точки
, если она определена в некоторой окрестности точки 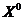 и в самой этой точке, и если
и в самой этой точке, и если  , то есть
, то есть 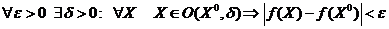 .
.
Частные производные.
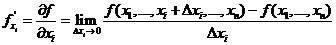 .
.
Этот предел, если он существует, называется частной производной функции 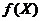 .
.
Дифференцируемость функции многих переменных.
Опр. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 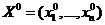 , если ее приращение можно представить в виде
, если ее приращение можно представить в виде 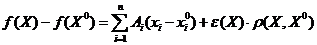 ,
,
где: 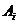 - не зависит от
- не зависит от  ;
; 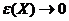 при
при  ;
; 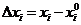 ;
; 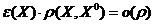 .
.
Теор. (Необходимое условие дифференцируемости). Если функция  дифференцируема в точке
дифференцируема в точке 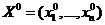 , тогда она имеет в этой точке все частные производные.
, тогда она имеет в этой точке все частные производные.
Док. Пусть 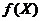 дифференцируема в точке
дифференцируема в точке 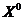 , то есть
, то есть 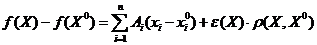 . Пусть
. Пусть  . Тогда
. Тогда 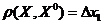 ,
, 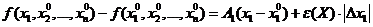 . Следовательно существует предел
. Следовательно существует предел 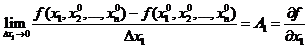 . Аналогично доказывается для
. Аналогично доказывается для  .
.
Теор. (Достаточное условие дифференцируемости). Если все частные производные  определены в окрестности точки
определены в окрестности точки 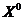 и непрерывны в ней, тогда
и непрерывны в ней, тогда 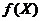 дифференцируема в точке
дифференцируема в точке 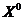 .
.
Док. Рассмотрим приращение функции двух переменных. 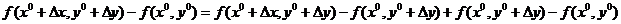 .
.
Используя два раза теорему Лагранжа о среднем и непрерывность частных производных, последнее выражение представим в виде 
 .
.
Здесь: 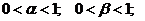
 при
при  .
.
Раскрывая скобки и группируя слагаемые, имеем  .
.
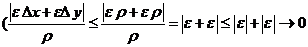 при
при 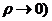 .
.
Таким образом, приращение функции представлено в виде 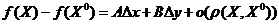 , где
, где  - являются частными производными и не зависят от
- являются частными производными и не зависят от 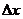 и
и 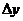 . Теорема доказана.
. Теорема доказана.
Замечание. Непрерывность частных производных не является необходимым условием дифференцируемости. Рассмотрим функцию двух переменных
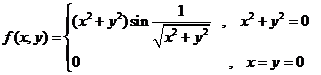 .
.
Функция дифференцируема в точке 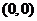 , так как
, так как 
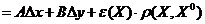 .
.
Частная производная  не имеет предела при
не имеет предела при 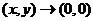 и, следовательно, не является непрерывной в точке
и, следовательно, не является непрерывной в точке 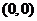 .
.
Теор. (Необходимое и достаточное условие дифференцируемости). Функция  дифференцируема в точке тогда и только тогда, когда в некоторой окрестности точки
дифференцируема в точке тогда и только тогда, когда в некоторой окрестности точки 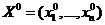 ее можно представить в виде:
ее можно представить в виде: 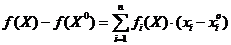 , где
, где 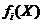 - некоторые непрерывные в точке
- некоторые непрерывные в точке 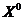 функции.
функции.
Док. Из дифференцируемости имеем 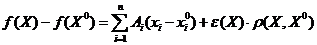 . Так как
. Так как 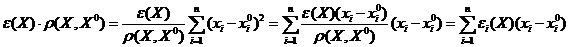 . Доопределив функцию
. Доопределив функцию 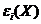 в точке
в точке 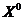 нулем, получим непрерывную функцию
нулем, получим непрерывную функцию 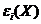 . Таким образом, имеем
. Таким образом, имеем 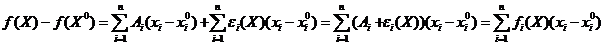 .
.
Обратно, из равенства в формулировке теоремы, используя непрерывность функций 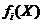 в точке
в точке 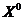 , т.е.
, т.е. 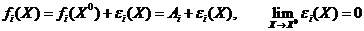 , получаем
, получаем  . Действительно
. Действительно 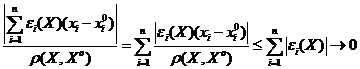 при
при  . Теорема доказана.
. Теорема доказана.
Дифференцирование сложной функции.
Теор. Пусть 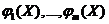 дифференцированы в точке
дифференцированы в точке  и функция
и функция  дифференцируема в точке
дифференцируема в точке 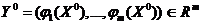 . Тогда сложная функция
. Тогда сложная функция  дифференцированы в точке
дифференцированы в точке 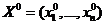 , причем
, причем 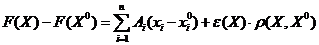 , где:
, где: 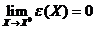 ;
; 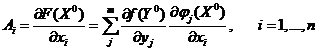 .
.
Док. Имеем 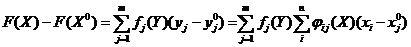 . Так как
. Так как 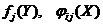 некие непрерывные функции, тогда
некие непрерывные функции, тогда 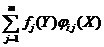 тоже непрерывная функция, а значит
тоже непрерывная функция, а значит 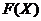 дифференцируема. В силу равенств
дифференцируема. В силу равенств 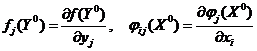 частную производную можно записать в виде
частную производную можно записать в виде 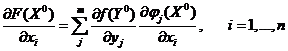 . Теорема доказана.
. Теорема доказана.
Дифференциал. Инвариантность формы первого дифференциала.
Опр. Пусть 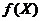 дифференцируема в точке
дифференцируема в точке 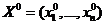 , тогда линейная относительно
, тогда линейная относительно  часть приращения этой функции называется дифференциалом
часть приращения этой функции называется дифференциалом  .
.
Найдем дифференциал сложной функции  .
.
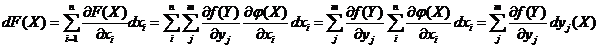 .
.
Таким образом, форма записи первого дифференциала не зависит от того, зависимыми или независимыми являются переменные.
Геометрический смысл дифференциала. Касательная плоскость к графику функции двух переменных. Вектор нормали к ней.
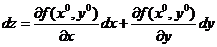 - дифференциал.
- дифференциал.
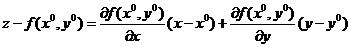 - уравнение касательной плоскости.
- уравнение касательной плоскости.
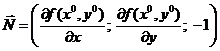 - вектор нормали.
- вектор нормали.
Частные производные и дифференциалы высших порядков.
Продифференцировав частные производные первого порядка по  или по
или по  , получим производные второго порядка:
, получим производные второго порядка:  ;
; 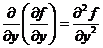 ;
;  ;
; 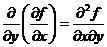 .
.
Теор. (О смешанных производных). Пусть 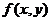 определена вместе со своими частными производными
определена вместе со своими частными производными 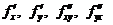 в некоторой окрестности точки
в некоторой окрестности точки  , причем
, причем 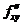 и
и 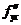 непрерывны в этой точке, тогда
непрерывны в этой точке, тогда 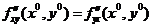 .
.
Док.  - приращение функции по переменной
- приращение функции по переменной  . Возьмем от приращения функции по
. Возьмем от приращения функции по  приращение по
приращение по 

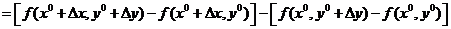 . Последнее выражение можно рассматривать как приращение вспомогательной функции
. Последнее выражение можно рассматривать как приращение вспомогательной функции 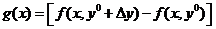 по переменной
по переменной  , поэтому, применяя к этому приращению теорему о среднем Лагранжа, получим
, поэтому, применяя к этому приращению теорему о среднем Лагранжа, получим 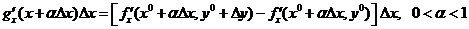 . К выражению в квадратных скобках снова применим теорему Лагранжа как к приращению функции
. К выражению в квадратных скобках снова применим теорему Лагранжа как к приращению функции  по переменной
по переменной  и получим
и получим 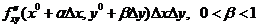 . Аналогично
. Аналогично  . Приравниваем полученные выражения и переходим к пределу при
. Приравниваем полученные выражения и переходим к пределу при 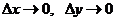 . Учитывая непрерывность производных
. Учитывая непрерывность производных 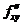 и
и 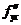 , получим требуемое равенство
, получим требуемое равенство 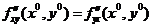 . Теорема доказана.
. Теорема доказана.
Пусть 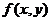 имеет непрерывные вторые частные производные в точке
имеет непрерывные вторые частные производные в точке  , а, значит, ее первые частные производные дифференцируемы в этой точке. Возьмем дифференциал от первого дифференциала, считая
, а, значит, ее первые частные производные дифференцируемы в этой точке. Возьмем дифференциал от первого дифференциала, считая 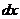 и
и 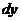 константами,
константами,  .
.
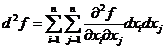 .
. 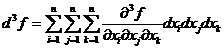 .
.
Формула Тейлора.
Пусть функция 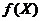 имеет в окрестности точки
имеет в окрестности точки 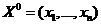 непрерывные частные производные до
непрерывные частные производные до 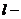 той включительно. Тогда ее можно разложить в окрестности точки
той включительно. Тогда ее можно разложить в окрестности точки 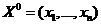 по формуле Тейлора
по формуле Тейлора  , где
, где 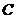 - точка, лежащая на прямой между точками
- точка, лежащая на прямой между точками 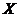 и
и 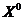 . Последнее слагаемое называется остаточным членом в форме Лагранжа. Данная формула совпадает с формулой Тейлора для функции одной переменной, если последнюю записать через дифференциалы. Формулу Тейлора можно записать и с остаточным членом в форме Пеано
. Последнее слагаемое называется остаточным членом в форме Лагранжа. Данная формула совпадает с формулой Тейлора для функции одной переменной, если последнюю записать через дифференциалы. Формулу Тейлора можно записать и с остаточным членом в форме Пеано 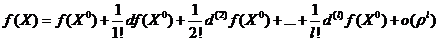 .
.
Экстремумы.
Опр. Функция 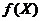 имеет в точке
имеет в точке 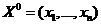 локальный максимум (минимум), если
локальный максимум (минимум), если  . В случае строгих неравенств экстремумы называются строгими.
. В случае строгих неравенств экстремумы называются строгими.
Теор. (Необходимое условие экстремума). Пусть 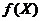 имеет экстремум в точке
имеет экстремум в точке 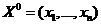 , тогда, если существуют частные производные первого порядка
, тогда, если существуют частные производные первого порядка 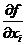 , то они равны нулю в этой точке.
, то они равны нулю в этой точке.
Док. Зафиксируем все переменные кроме 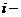 той. Получим функцию одной
той. Получим функцию одной 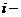 той переменной, которая имеет экстремум, а, значит, ее производная, согласно теореме Ферма, равна нулю. Теорема доказана.
той переменной, которая имеет экстремум, а, значит, ее производная, согласно теореме Ферма, равна нулю. Теорема доказана.
Замечание. Если функция 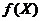 имеет экстремум в точке
имеет экстремум в точке 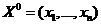 и дифференцируема в этой точке, а, значит, имеет все производные первого порядка, тогда
и дифференцируема в этой точке, а, значит, имеет все производные первого порядка, тогда 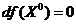 .
.
Равенство нулю частных производных первого порядка не является достаточным для существования экстремума. Чтобы убедиться в этом, достаточно рассмотреть простую функцию 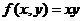 .
.
Опр. Квадратичная форма 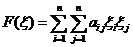 называется:
называется:
а) положительно определенной квадратичной формой, если 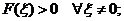
б) отрицательно определенной квадратичной формой, если 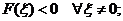
в) неопределенной квадратичной формой, если 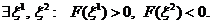
Критерий Сильвестра. Квадратичная форма положительно определена в том и только том случае, когда все главные миноры ее матрицы положительны 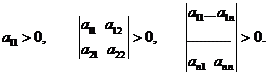
Квадратичная форма отрицательно определена, если  положительно определена. Утверждение. Если квадратичная форма положительно определена, то найдется такое положительное число
положительно определена. Утверждение. Если квадратичная форма положительно определена, то найдется такое положительное число 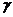 , что
, что 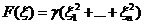 .
.
Действительно. Рассмотрим квадратичную форму 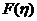 на сфере
на сфере  . Функция
. Функция 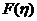 положительно определена и непрерывна на сфере (замкнутом ограниченном множестве), значит, принимает в некоторой точке сферы минимальное положительное значение
положительно определена и непрерывна на сфере (замкнутом ограниченном множестве), значит, принимает в некоторой точке сферы минимальное положительное значение 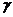 . Если
. Если 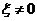 , то точка
, то точка  принадлежит сфере, поэтому
принадлежит сфере, поэтому  . Используя однородность квадратичной формы, получаем
. Используя однородность квадратичной формы, получаем  , то есть
, то есть 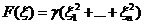 .
.
Теор. (Достаточное условие экстремума). Пусть функция 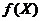 имеет в окрестности точки
имеет в окрестности точки 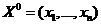 непрерывные частные производные второго порядка, и пусть
непрерывные частные производные второго порядка, и пусть 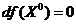 . Тогда, если
. Тогда, если 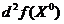 - положительно определенная квадратичная форма, то
- положительно определенная квадратичная форма, то 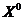 - точка строгого минимума, если
- точка строгого минимума, если 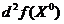 - отрицательно определенная квадратичная форма, то
- отрицательно определенная квадратичная форма, то 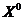 - точка строгого максимума, если
- точка строгого максимума, если 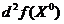 - неопределенная квадратичная форма, то в точке
- неопределенная квадратичная форма, то в точке 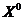 нет экстремума.
нет экстремума.
Док. Используя формулу Тейлора при 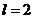 и тот факт, что
и тот факт, что 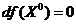 , запишем приращение функции
, запишем приращение функции 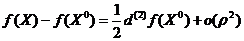 .
.
Пусть  является положительно определенной квадратичной формой, тогда в силу последнего утверждения найдется такое положительное число
является положительно определенной квадратичной формой, тогда в силу последнего утверждения найдется такое положительное число 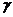 , что
, что  . Теперь приращение функции можно записать в виде
. Теперь приращение функции можно записать в виде 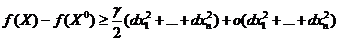 . Последний член в неравенстве более высокого порядка малости при
. Последний член в неравенстве более высокого порядка малости при  , чем предпоследний. Поэтому найдется окрестность точки
, чем предпоследний. Поэтому найдется окрестность точки 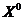 , в которой предпоследний член превзойдет последний по модулю, и мы получим
, в которой предпоследний член превзойдет последний по модулю, и мы получим 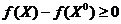 , то есть в точке
, то есть в точке 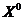 будет наблюдаться локальный минимум. Аналогично доказывается для отрицательно определенной квадратичной формы. Для неопределенной квадратичной формы доказывается методом от противного. Теорема доказана.
будет наблюдаться локальный минимум. Аналогично доказывается для отрицательно определенной квадратичной формы. Для неопределенной квадратичной формы доказывается методом от противного. Теорема доказана.
Условный экстремум.
Пусть задана функция 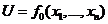 и уравнения связи
и уравнения связи 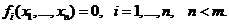
Опр. Функция 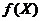 имеет в точке
имеет в точке 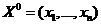 условный максимум (минимум), если
условный максимум (минимум), если 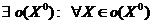 и удовлетворяющим уравнениям связи выполняется неравенство
и удовлетворяющим уравнениям связи выполняется неравенство 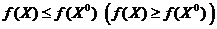 . В случае строгих неравенств условные экстремумы называются строгими.
. В случае строгих неравенств условные экстремумы называются строгими.
Прямой метод отыскания условного экстремума.
Предположим, что из системы уравнений связи можно выразить какие-либо 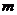 переменных через остальные
переменных через остальные 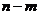 переменных. Тогда, подставив их в
переменных. Тогда, подставив их в 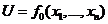 получим функцию
получим функцию 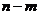 переменных. Задача отыскания условного экстремума сводится, таким образом, к отысканию обычного экстремума.
переменных. Задача отыскания условного экстремума сводится, таким образом, к отысканию обычного экстремума.
Наибольшие и наименьшие значения функции.
Пусть непрерывная функция 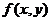 определена в некоторой ограниченной замкнутой области, граница которой задается уравнением
определена в некоторой ограниченной замкнутой области, граница которой задается уравнением 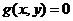 . Наибольшие и наименьшие значения функция
. Наибольшие и наименьшие значения функция 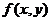 может принимать в точках экстремума (внутри области) и на границе области в точках условного экстремума функции
может принимать в точках экстремума (внутри области) и на границе области в точках условного экстремума функции 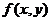 с уравнением связи
с уравнением связи 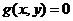 .
.
Неявные функции.
Рассмотрим уравнение 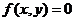 . Множество точек плоскости, координаты которых удовлетворяют этому уравнению, можно назвать графиком уравнения. Например, множеством точек, удовлетворяющих уравнению
. Множество точек плоскости, координаты которых удовлетворяют этому уравнению, можно назвать графиком уравнения. Например, множеством точек, удовлетворяющих уравнению  , является окружность единичного радиуса. Верхняя часть этой окружности соответствует функции
, является окружность единичного радиуса. Верхняя часть этой окружности соответствует функции 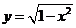 , нижняя часть окружности определяется функцией
, нижняя часть окружности определяется функцией 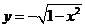 .
.
Теор. Пусть непрерывная функция 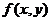 имеет в окрестности точки
имеет в окрестности точки  непрерывные производные
непрерывные производные 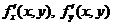 и при этом
и при этом 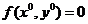 ,
, 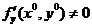 , тогда существует прямоугольник
, тогда существует прямоугольник 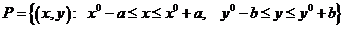 в котором функция
в котором функция 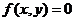 определяет
определяет  как неявную функцию
как неявную функцию  . Функция
. Функция 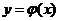 - непрерывно дифференцируема на интервале
- непрерывно дифференцируема на интервале  и
и 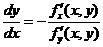 .
.
Вопросы к коллоквиуму (2 семестр, гр. МП – 16, 17, 17а, 18, 19)
1.Несобственные интегралы. Критерий Коши сходимости несобственных интегралов.
2.Несобственные интегралы. Их свойства.
3.Необходимое и достаточное условие сходимости несобственных интегралов от неотрицательных функций.
4.Признак сравнения.
5. Предельный признак сравнения.
6.Открытые, замкнутые, ограниченные, связные множества.
7.Предел функции. Критерий Коши существования конечного предела.
8.Непрерывность функции в точке.
9.Дифференцируемость функции. Необходимое условие дифференцируемости.
10.Достаточное условие дифференцируемости.
11.Необходимое и достаточное условие дифференцируемости.
12.Дифференцирование сложной функции.
13.Дифференциал. Инвариантность формы первого дифференциала.
14.Касательная плоскость к графику функции двух переменных. Вектор нормали.
15.Теорема о смешанной производной.
16.Формула Тейлора.
17.Экстремум функции. Необходимое условие экстремума.
18.Достаточное условие экстремума.
19.Условный экстремум. Прямой метод отыскания условного экстремума.
20.Теорема о неявной функции.