Методика построения асимптотических ЛАХ разомкнутой одноконтурной системы по известной передаточной функции, записанной в виде произведения передаточной функции типовых звеньев, состоит в следующим.
Пусть получена передаточная функция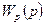 
разомкнутой одноконтурной системы автоматического управления (САУ) в виде произведения передаточных функций типовых звеньев, имеющая следующий общий вид:
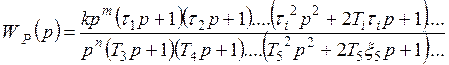(2)
где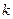 
- общий коэффициент усиления последовательно соединенных звеньев.
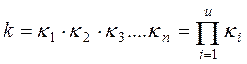
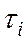- постоянная времени i – того звена.
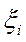- показатель колебательности i – того звена второго порядка.
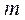- число идеальных дифференцирующих звеньев.
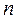- число идеальных интегрирующих звеньев.
При n>m разность между числами идеальных интегрирующих звеньев и числом идеальных дифференцирующих звеньев в САУ определяет порядок астатизма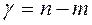 
Дальнейший порядок построения асимптотической ЛАХ по передаточной функции (2) может быть представлен в виде следующего алгоритма:
1. Привести исходную структуру к структуре с единичной обратной связью, для чего перенести элемент ГОС в прямую цепь.
2. Разомкнуть систему и определить передаточную функцию разомкнутой САУ, считая за выходную координату сигнал ГОС.
3. Определить частоту, при которой низкочастотная асимптота ЛАХ пересекает ось частот. Если система содержит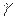 
идеальных интегрирующих звеньев, то низкочастотная асимптота пересекает ось частот при частоте:
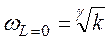, (3)
где k – коэффициент передачи разомкнутой системы.
Если система содержит m идеальных дифференцирующих звеньев, то низкочастотная асимптота пересекает ось частот при частоте:
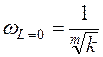. (4)
Построить низкочастотную асимптоту с наклоном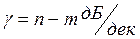 
.
4. Определяются частоты сопряжения 
для входящих в передаточную функцию 
типовых динамических звеньев с постоянными времени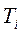 
.
|
|
Найденные значения частот в логарифмическом масштабе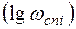 
откладывается по оси частот по мере их возрастания.
5. Первая асимптота ЛАХ с определенным ранее наклоном (см. п. 2) проводится до наименьшей частоты сопряжения.
6. В этой точке, абсцисса которой соответствует достигнутой ЛАХ частоты сопряжения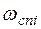 
, соответствующей конкретной постоянной времени 
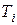определенного типового звена, входящего в исследуемую САУ, асимптота ЛАХ претерпевает излом на:
а) –20дБ/дек, если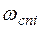 
соответствует постоянной времени 
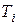, входящей в инерционное звено;
б) +20дБ/дек, если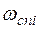 
соответствует постоянной времени 
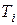, входящей в форсирующее звено;
в) –40дБ/дек, если 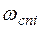соответствует постоянной времени 
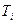, входящей в колебательное звено;
г) +40дБ/дек, если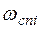 
соответствует постоянной времени 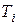, входящей в операторный полином звена второго порядка с показателем колебательности 
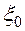< 1, стоящей в числителе передаточной функции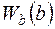 
7. Полученная асимптота ЛАХ, имеющая наклон, определенный в предыдущем пункте, продлевается до следующей частоты сопряжения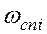 
.
8. В этой точке, абсцисса которой соответствует достигнутой частоте сопряжения, вновь повторяется процедура изложенная в пункте 6.
9. Пользуясь кривыми поправок (номограммы отклонения), уточнить полученную асимптотическую ЛАХ. Поправки для звеньев, частоты сопряжения которых отличается друг от друга не более чем 2-3 октавы, складываются алгебраически.
Точная ЛАХ колебательного звена практически перестает отличатся от асимметрической при отклонении в обе стороны от частоты сопряжения на 2-3 октавы
|
|
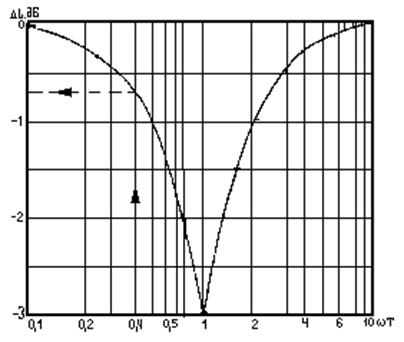
Рисунок 3. Номограммы для уточнения отклонение точной ЛАХ апериодического звена от асимптотической
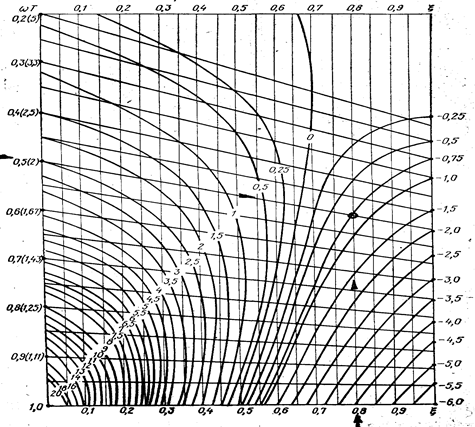
Рисунок 4. Номограммы для уточнения отклонение точной ЛАХ колебательного звена от асимптотической
Фазовая частотная характеристика разомкнутой одноконтурной системы определяется как сумма ФЧХ каждого типового звена на фиксированных частотах
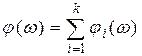. (5)
Пример 2.1.1. Построить ЛАХ и ЛФХ системы автоматического управления, если передаточная функция разомкнутой системы имеет вид
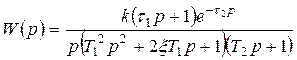, (6)
где k=100 c-1; 
=1,8 с; Т1=0,6 с;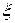 
=0,35; Т2=0,1 с; 
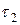=0.05 с.
Решение.
Частоты сопряжения
;
;
.
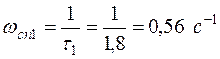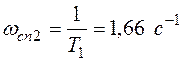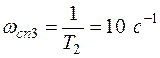Частота при которой низкочастотного асимптоты пересекает ось частот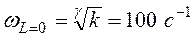 
Наклон низкочастотный асимптоты равен -20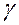 
=-20×1=-20 дБ/дек.
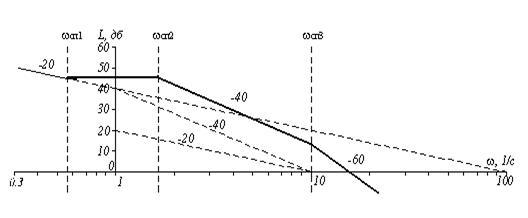
Рисунок 5. ЛАХ системы
Максимальное отклонение точной ЛАХ от асимптотической для колебательного звена имеет место при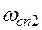 
=1,66 и равно
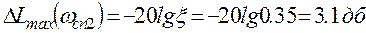. (7)
Значение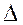 
Lmах(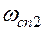
) может быть определено по номограмме.
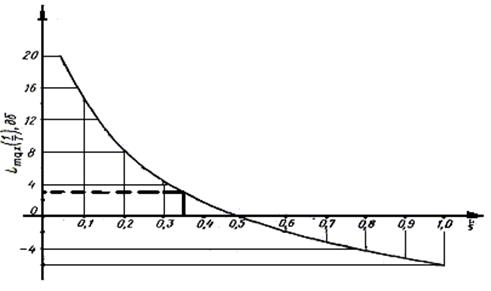
Рисунок 6. Номограмма для определения резонансного типа ЛАХ колебательного звена.
Пример 2.1.2. Для апериодического звена 1-вого порядка с передаточной функцией
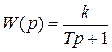. (8)
показать, что:
1) точная ЛАХ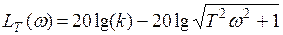 
имеет две асимптоты;
2) частота сопряжения асимптотической ЛАХ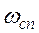 
= 
;
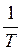3) наклон одной асимптоты 0 дБ/дек, наклон второй –{ -20дБ/дек };
4) наибольшее отклонение асимптотической ЛАХ La(
) от точной LТ() не превышает 3дБ.
Решение.
АЧХ звено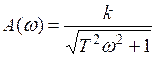 
,следовательно выражение для точной ЛАХ имеет вид:
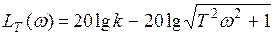. (9)
Точная ЛАХ строится по точкам при различных фиксированных значениях частоты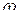 
и приведена на рисунке 7 (для определённости построения принято k=100, T=0.02)
|
|
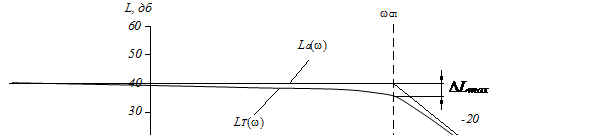
Рисунок 7. Логарифмические характеристики апериодического звена первого порядка
Если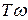 
<<1, то произведением 
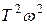можно пренебречь и в этом случае получим:
L1(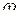
) 
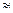20lgk, (10)
поскольку lg1=0.
При 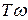<<1, единицей можно пренебречь, тогда подкоренное выражение равно 
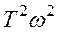и ЛАХ имеет вид:
L2(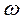
)=20lgk – 20lg(
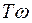). (11)
Так как при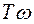 
<<1, точная ЛАХ LT(
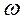) стремится к значению L1(
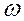)=20lgk, а при 
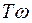>>1, LT(
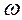) приближается к прямой L2(
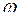)=20lgk-20lg(
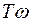), поэтому прямые L1(
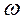)=20lgk и L2(
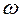)=20lgk-20lg(
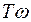) можно рассматривать как низкочастотную и высокочастотную асимптоты для точной ЛАХ 
.
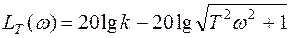Наклон низкочастотной асимптоты L1(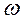
)=20lgk составляет 0 дБ/дек очевиден. Для определения наклона асимптоты L2(
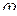)=20lgk-20lg(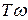) следует найти разность ординат при изменении частоты на одну декаду, т.е.
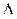L= L2(
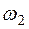) – L2(
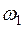), (12)
причем 
.
Подставив значение частоты, получим:
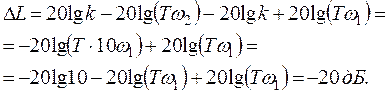(13)
Таким образом при изменении частоты на одну декаду изменение ординаты составляет – 20дБ, следовательно наклон асимптоты L2()=20lgk – 20lg(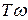) составляет – 20дБ.
Асимптоты L1(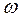
) и L2(
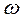) пересекаются в точке, для которой
L1(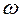)= L2(
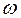) или 20lgk =20lgk – 20lg(T ). (14)
Таким образом для точки пересечения асимптот справедливы равенства:
20lg(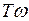
)=0, т.е. 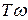=1. (15)
Таким образом, частота сопряжения 
.
Наибольшее отклонение точной ЛАХ LT(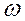
) от асимптотической Lа(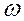) имеет место, когда неравенства 
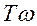<<1 и 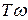>>1 обращаются в равенства, т.е. при частоте сопряжения 
.
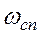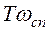= 1. (16)
Значение асимптотической ЛАХ при частоте сопряжения
Lа(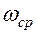
)= L1(
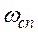)= 20lgk. (17)
Значение точной ЛАХ при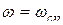 
:
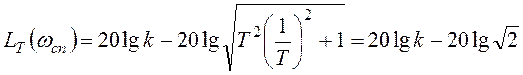. (18)
Следовательно
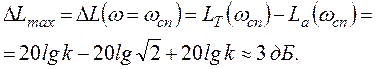(19)