Тема 4: Двумерные и многомерные случайные величины.
Для решения задач по данной теме необходимо освоить теоретический материал в соответствии с программой курса: раздел 4.2, подразделы 1 и 2. Для этого необходимо изучить разделы учебных пособий: [1], главы 7 – 8.
1. Решение типовой задачи. Рассмотрим задачу 14.
Из условий задачи следует, что двумерная плотность распределения:
 .
.
При нахождении одномерных распределений надо рассматривать два варианта: отрицательные и положительные значения варианты. Найдем распределение f (x). При x < 0 получим:

При x > 0 получим:
 /
/
Объединяем оба варианта:

Аналогично получим:
 .
.
Поскольку  , заключаем, что компоненты вектора зависимы.
, заключаем, что компоненты вектора зависимы.
Чтобы получить условное распределение f (x | y), надо рассечь поверхность распределения f (x, y) плоскостью, параллельной осям x и f. В результате получим прямоугольник, опирающийся на основание:  .
.
Ясно, что условное распределение равномерное. Из условия нормировки найдем:
 .
.
За пределами этого интервала:
 .
.
Задачи для самостоятельного решения.
Задача 1. Система случайных величин имеет плотность распределения

Найти: а) величину А; функцию распределения F (x, y).
Задача 2. Случайные величины X и Y связаны соотношением Mx + nY = c, где m, n, с - неслучайные величины. Найти коэффициент корреляции rxy и отношение sx/sy.
Задача 3. Определить математические ожидания и корреляционную матрицу системы случайных величин (X, Y), если плотность распределения

Задача 4. Система случайных величин (X,Y) имеет функцию распределения

Найти плотность распределения, математические ожидания и корреляционную матрицу
Задача 5. Дана плотность распределения случайной точки на плоскости:
 .
.
Найти: коэффициент с, корреляционную матрицу.
Задача 6. Координаты случайной точки на плоскости подчинены нормальному закону

Найти: вероятность того, что точка окажется внутри эллипса с главными полудиаметрами ka и kb, совпадающими с координатными осями Ox и Oy.
Задача 7. Система случайных величин подчиняется нормальному закону с параметрами МХ = МY = 0, DX = DY = 81, Kxy = 0. Найти вероятности того, что: а) X > Y > 0, б) X > 0, Y < 0.
Задача 8. Случайная точка распределена по нормальному круговому закону (r = 0) c средним квадратическим отклонением 10 м. Сравнить вероятности попадания точки в фигуру, площадь которой 314 м2, если она имеет форму: а)круга, б) квадрата, в) прямоугольника с отношением сторон 10:1. Центр рассеяния совпадает с центром фигуры..
Задача 9. Положение случайной точки (X,Y) равновероятно в любом месте эллипса с главными полудиаметрами а и b, совпадающими с осями координат Ох и Оy соответственно. Найти безусловные и условные плотности распределения, корреляционный момент.
Задача 10. Положение случайной точки (Х, Y) равновероятно в любом месте круга радиуса R, центр которого совпадает с началом координат. Определить плотность и функцию распределения каждой из прямоугольных координат. Являются ли координаты зависимыми?
Задача 11. Положение случайной точки (Х, Y) равновероятно в любом месте круга радиуса R, центр которого совпадает с началом координат. Вычислить корреляционную матрицу системы (Х, Y). Являются ли координаты (Х, Y) коррелированными?
Задача 12. Плотность распределения неотрицательных случайных величин (Х, Y) имеет вид
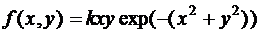
Найти коэффициент k, и безусловные и условные плотности распределения координат, первый и второй моменты распределения.
Задача 13. Дана плотность распределения случайной точки на плоскости:
 .
.
Найти: а) коэффициент k, корреляционную матрицу, б) условные математические ожидания и дисперсии, в) плотности распределения каждой из случайных величин, г) условные плотности распределения.
Задача 14. Случайная величина (X, Y) равномерно распределена внутри квадрата со стороной а, центр которого находится в начале координат, а стороны повернуты относительно осей на 45°. Найти одномерные распределения, условные распределения и выяснить, являются ли компоненты вектора зависимыми.
Задача 15. Дана плотность распределения случайной точки на плоскости:
 .
.
Найти: Найти: а) коэффициент k, корреляционную матрицу, б) условные математические ожидания и дисперсии, в) плотности распределения каждой из случайных величин, г) условные плотности распределения.
Задача 16. Дана плотность распределения случайной точки на плоскости:
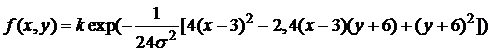 .
.
Найти: а) коэффициент k, корреляционную матрицу, б) условные математические ожидания и дисперсии, в) плотности распределения каждой из случайных величин, г) условные плотности распределения.
Задача 17. Дана плотность распределения случайной точки на плоскости:
 .
.
Найти: а) коэффициент k, корреляционную матрицу, б) условные математические ожидания и дисперсии, в) плотности распределения каждой из случайных величин, г) условные плотности распределения.
Задача 18. Система случайных величин имеет плотность распределения

Найти: а) величину А; функцию распределения F (x, y).
Задача 19. Случайные величины X и Y связаны соотношением Mx + nY = c, где m, n, с - неслучайные величины. Найти коэффициент корреляции rxy и отношение sx/sy.