1. Вычислить следующие пределы:
а)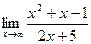 
.
Решение:
Имеем неопределенность 
. Чтобы избавиться от нее, разделим числитель и знаменатель на 
.
, так как при 
отношения 
стремятся к нулю.
б) 
.
Решение:
Неопределенность . Разделим числитель и знаменатель на 
.
.
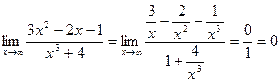в)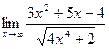 
.
Решение:
Неопределенность 
. Разделим числитель и знаменатель на 
.
.
г) 
.
Решение:
Неопределенность 
. Разложим числитель и знаменатель на множители, после сокращения на (х-2) получим:
.
д) 
.
Решение:
Неопределенность 
. Приведем выражение в скобках к общему знаменателю.
.
е) 
.
Решение:
Неопределенность . Умножим и разделим выражение в скобках на сопряженное ему (
).
.
ж) 
.
Решение:
Неопределенность . Подвергаем функцию преобразованию с тем, чтобы использовать первый замечательный предел
.
.
з) 
.
Решение:
Неопределенность . Обозначим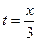 
. Следовательно х=3t. При 
. Перейдем к новой переменной.
.
и) 
.
Решение:
Неопределенность . Воспользуемся формулой тригонометрического тождества 1- cosx = 
. Следовательно, 
.
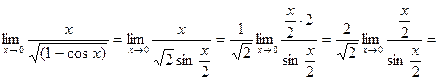
к) 
.
Решение:
Неопределенность . Выполним элементарное преобразование.
.
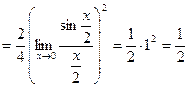л) 
.
Решение:
Неопределенность . Обозначим 
, тогда 
. Если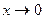 
, то и 
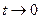. Следовательно,
.
м) 
.
Решение:
Неопределенность 
. Воспользуемся вторым замечательным пределом.
.
м) 
.
Решение:
Неопределенность . Выполним элементарные преобразования и воспользуемся вторым замечательным пределом.
.
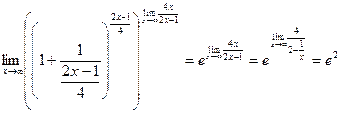2. Пользуясь таблицей производных, найти производные следующих функций:
а) 
.
Решение:
.
б) 
.
Решение:
.
в) 
.
Решение:
.
г) 
.
Решение:
.
д) 
.
Решение:
.
е) 
.
Решение:
.
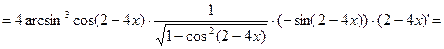
ж) 
.
Решение:
.
з) 
.
Решение:
.
и)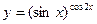 
.
Решение:
.
.
.
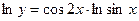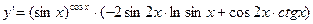3. Исследовать функцию, построить ее график 
.
Решение:
1. Область определения 
, т.е. 
.
2. Функция четная, так как 
, и ее график симметричен относительно оси ординат.
3. Вертикальные асимптоты могут пересекать ось абсцисс в точках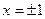 
. Так как пределы функции при 
(слева) и при 
(справа) бесконечны, т.е.
и 
, то прямая х=1 есть вертикальная асимптота. В силу симметрии графика 
х=-1 также вертикальная асимптота.
4. Исследуем поведение функции в бесконечности. Вычислим 
. В силу четности имеем 
, т.е. прямая у=-1 - горизонтальная асимптота.
Т.к. 
, то наклонных асимптот нет.
5. Найдем экстремумы и интервалы монотонности функции.
;
у’=0 при х=0 и у’ не существует при .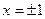
Однако критической является только точка х=0 (так как значения 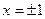не входят в область определения функции). Поскольку при 
, а при 
, то х=0 – точка минимума и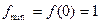 
- минимум функции. На интервалах 
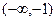и 
функция убывает, на интервалах 
и 
- возрастает.
6. Найдем интервалы выпуклости функции и точки перегиба.
.
на интервале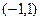 
и функция выпукла вниз на этом интервале.
на интервалах 
, и на этих интервалах функция выпукла вверх. Точек перегиба нет.
7. Найдем точки пересечения с осями. 
, т.е. точка пересечения с осью ординат (0,1). Уравнение 
решений не имеет, следовательно, график функции не пересекает ось абсцисс.
График функции изображен на рисунке 2.
Рис. 2
4. Найти полный дифференциал функции
а)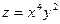 
Решение:
Пользуясь формулой для полного дифференциала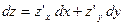 
, находим
, 
.
Отсюда 
.
б) 
Решение:
, 
.
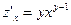Отсюда 
.
в)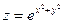 
Решение:
, 
.
Отсюда 
.
5. Вычислить неопределенные интегралы:
а) 
Решение:
Сделаем подстановку: 
, откуда 
.
Поэтому 
. Сделав обратную подстановку, получим 
.
б) 
Решение:
Подведем х2 под знак дифференциала и воспользуемся формулой: 
.
.
в) 
Решение:
Как и в предыдущем примере подведем х2 под знак дифференциала, но воспользуемся формулой: 
.
.
г) 
Решение:
Сделаем подстановку t=arcsin2x. Продифференцировав обе части последнего равенства, получим: 
, поэтому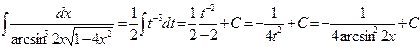 
.
д) 
Решение:
Сделаем подстановку 
. Продифференцировав обе части последнего равенства, получим: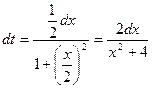 
, поэтому 
.
е) 
Решение:
Данный интеграл можно найти интегрированием по частям, полагая 
. Тогда 
.
Применим формулу интегрирования по частям: 
, тогда 
.
ж) 
Решение:
Данный интеграл можно найти интегрированием по частям, полагая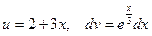 
. Тогда 
.
Применяя формулу интегрирования по частям, получим
.
з) 
Решение:
Данный интеграл можно найти интегрированием по частям, полагая 
. Тогда 
.
Применяя формулу интегрирования по частям, получим
.
и) 
Решение:
Выполним сначала замену переменной 
. Тогда 
и 
. Следовательно,
.
Пусть 
. Тогда 
, 
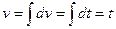. Применяя формулу интегрирования по частям, получим
.
Полагая в формуле интегрирования по частям 
, получаем 
. Окончательно имеем 
.
к) 
Решение:
Применим формулу: 
.
Тогда 
.
л) 
Решение:
Поскольку 
, то используем замену 
. Тогда 
и 
.
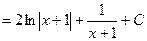м) 
Решение:
Так как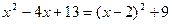 
, то положим 
.
Тогда 
и 
.
Первый из интегралов табличный. Второй интеграл можно свести к табличному, если внести под знак дифференциала t.
.
н) 
Решение:
Учитывая, что 
, положим 
. Эта замена позволяет свести искомый интеграл к табличному.
.
о) 
Решение:
Так как 
, то положим 
.
Тогда 
, следовательно,
.
Первый из интегралов табличный. Второй интеграл можно свести к табличному, если внести под знак дифференциала t.
.
6. Вычислить площадь фигуры ограниченной линиями
а) 
, х=0, у=4.
Решение:
Рис. 3
Из чертежа (см. рис. 3) видно, что искомая площадь S криволинейного треугольника ОАВ равна разности двух площадей:
,
каждая из которых находится по геометрическому смыслу определенного интеграла. Решая систему 
, получаем, что точка В пересечения прямой у=4 и кривой 
имеет координаты (2; 4). Тогда
,
.
Окончательно 
(ед.2).
б) 
, 
.
Решение:
Рис. 4
Координаты точек пересечения кривых, найдем решая систему 
. Это точки (-1; 3) и (2; 0). Искомая площадь (см. рис. 4)- это площадь фигуры, заключенной между кривыми; при этом на отрезке 
. Следовательно,
(ед.2).
7. Найти общее решение (общий интеграл) дифференциального уравнения
а)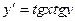 
Решение:
Разделим переменные:
.
Проинтегрируем обе части последнего равенства
.
По свойству логарифмов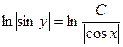 
. Тогда окончательное решение дифференциального уравнения имеет вид:
.
б) 
Решение:
Разделив левую и правую части уравнения на выражение 
(при 
), приходим к равенству 
. Интегрируя, получим
.
Решение перепишем в виде 
или 
, где 
.
в) 
Решение:
В результате разделения переменных получаем 
.
Интегрируя получим 
.
Общее решение можно записать в виде 
.
г) 
Решение:
Для отделения переменных представим уравнение в виде 
.
Разделим обе части уравнения на 
. В результате получим 
. Переменные разделились.
Интегрируем это уравнение:
. Отсюда, находим общий интеграл уравнения в виде 
.
д)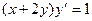 
Решение:
Положим 
. Тогда 
, откуда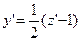 
и исходное уравнение приводится к виду 
, которое допускает разделение переменных.
Выражая из последнего равенства z’, получаем 
и, следовательно, 
.
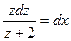Интегрируем это уравнение:
.
Возвращаясь к первоначальным переменным, получаем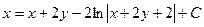 
или 
, где 
.