Образ и ядро линейного оператора

Взаимное расположение двух прямых

Если прямые заданы уравнениями и 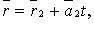то они:

1) параллельны (но не совпадают)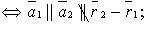

2) совпадают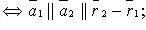

3) пересекаются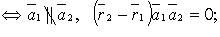

4) скрещиваются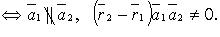

 

22.

Взаимное расположение прямой и плоскости

 

Плоскость 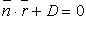и прямая

1) пересекаются

2) прямая лежит в плоскости

3) параллельны

Если 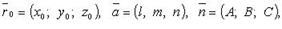то случаи 1 - 3 имеют место, когда:

1)

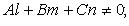
2)

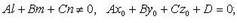
3)

 

 

 

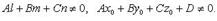
23.

Линейным или векторным пространством называется совокупность ɀ
объектов произвольной природы которые называются элементами пространства и для которых определены опереции сложения и умножения на число
Свойства а+в=в+а; αа=αв а=в;
(а+в)+с=а+(в+с)=а+в+с;а+0=а;
(αβ)а=α(βа); (α+β)а= αа+βа;
а*0=0;а+х=в х-решение единственное
эл-т в при котором а+в=0 только один
нейтральный эл-т в линейном пространстве только один

Базисом линейного пространства L называется система элементов принадлежащих L, удовлетворяющая двум условиям:
1)система (е1, к, еn) линейно независима.
2)Любой элемент L линейно выражается через базисные (т.е. является линейной комбинацией элементов(e1. e2 k en)
Размерностью линейного пространства L (обозначается dim L) называется максимальное число линейно независимых элементов этого пространства. Если такого числа не существует – пространство называется бесконечномерным.
Теорема 4. Размерность линейного пространства равна числу базисных векторов.
Подпространством линейного пространства L называется такое подмножество элементов L, которое само является линейным пространством. Т.е. подпространство замкнуто относительно операций сложения и умножения на число. (все аксиомы выполняются автоматически).

 

 

 

25.

Евклидово пространство-линейное пространство в котором зафиксированно некоторое сколярное произведение.
Неравенство |(х,у)|<=|х||у|

Линейное пространство E = {f, g, h, …} называется евклидовым, если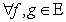

ставится в соответствие число, называемое скалярным произведением: 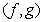. При этом,

для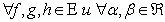
выполняются аксиомы:

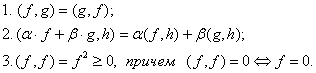
Для любых векторов x и y евклидова пространства E со скалярным призведением (x, y) справедливо неравенство:

|(x, y)| ² ≤ (x, x)·(y, y).

 

 

26.

Векторы x и y пространства со скалярным произведением L

называются ортогональными, если (x, y)=0. В этом случае пишут x﬩y.

 

 

Пусть векторы х1…хк образуют ортогональную систему векторов, тогда они линейно независимы α1х1+…+αкхк=0
Если ортогональная сис-ма содержит n векторов, то т.к. они ЛН, то могут быть приняты за базис ὲⁿ. Такой базис ортогональный.
В любом евклидовом пространстве существуют ортонормированные базисы.
По ним можно построить ортогональную систему.
. Если -- счетная система линейно независимых векторов в линейном пространстве со скалярным произведением L, то новые последовательности

обладают следующими свойствами:

1) система 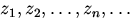ортонормирована, т. е. любые два ее вектора ортогональны и каждый вектор имеет единичную длину;

 

 

 

 

 

27..

Оператор A, действующий в пространстве Rⁿ называется линейным оператором, если для любых 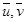из Rⁿ и для любого числа α справедливо:

и .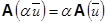

Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rⁿ —

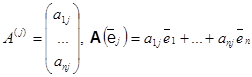
называется матрицей линейного оператора A в данном базисе.

28.

Образ и ядро линейного оператора

Рассмотрим линейный оператор 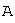, действующий в конечномерном линейном пространстве 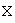. Доказано, что образ линейного оператора 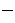линейное пространство. Размерность образа линейного оператора называется рангом оператора, обозначается . Ядром линейного оператора называется множество элементов из 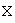, образом которых является нулевой элемент. Ядро оператора обозначают 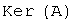: 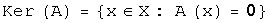Ядро линейного оператора 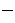линейное пространство; размерность ядра линейного оператора называется дефектом оператора, обозначается : .

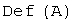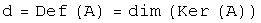Для линейного оператора, действующего в n-мерном линейном пространстве 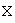, справедливы следующие утверждения:

сумма ранга и дефекта оператора равно размерности пространства, в котором действует оператор: ;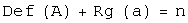

ранг оператора равен рангу его матрицы;

ядро оператора совпадает с множеством решений линейной однородной системы с матрицей 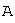, размерность пространства решений этой системы равна дефекту оператора, а ее фундаментальная система решений образует базис в ядре оператора;

столбцы, входящие в базисный минор матрицы оператора образуют базис в образе оператора.

 

29.

Пусть в n-мерном линейном пространстве L выбран базис e1 e2 en, который мы будем для удобства называть "старый" и другой базис e1’ e2’ en’, который мы будем называть "новый". Возьмем призвольный вектор 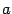из 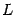. Его координатный столбец в старом базисе обозначим

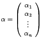, а в новом -- 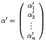. Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

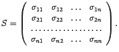Эта матрица называется матрицей перехода от старого базиса к новому. 1 Пусть 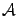-- линейное преобразование пространства 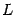, и -- матрицы этого преобразования в старом и новом базисе соответственно. Тогда

 

 

 

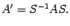
30.

A — линейный оператор в евклидовом пространстве E и A — его матрица в некотором ортонормированном базисе в E, то у оператора есть единственный сопряженный оператор, причем матрица сопряженного оператора в том же базисе — это матрица A^T.
Линейный оператор А называется симметрическим или самосопряженным, если в ортонормированном базисе он имеет симметричную матрицу:

. Если линейный оператор A, действующий в евклидовом пространсте E, таков, что для любых 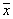и 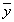из E справедливо 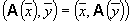, то оператор A называется сопряженным оператором.
1) сопряженный оператор существует для любого оператора А
2) он единственный и линейный
3)Матрица сопр. Оператора в ортонормированном базисе есть А^Т по отношению к матрице А
св-во операции сопряжения
1) (А^*)^*=А 2) (αА)^*= α А^*
3) (А+В)^* =А^* + В^* 4) (АВ)^* = В^*А^*
Если оператор А-самосопр, е1,…,еn ортонормированный базис
В ортонорм базисе матрицы операторов симметрические, то они сопряженные

 

 

31.

Одной из важнейших задач линейной алгебры является поиск оптимального базиса для конкретного линейного оператора в данном пространстве. Эта задача сводится к поиску собственных векторов и собственных значений данного оператора. Следует отметить, что в общем случае она решения не имеет.

Постановка задачи: Требуется найти такие векторы x≠0,x?L называемые собственными векторами линейного оператора А и числа λ?R, называемые собственными значениями оператора, которые удовлетворяют условию: A(x)=λx. Для определения величин λ получаем характеристическое уравнениие=0. 1)Собственные значения линейного оператора не зависят от базиса.2) Матрица линейного оператора в собственном базисе имеет диагональный вид, причем на диагонали стоят собственные значения.2) Собственные векторы х1,К,хm соответствующие попарно различным собственным значениям λ1,К,λm линейно независимы. 4) Собственные векторы, соответствующие одному собственному значению, образуют линейное подпространство.

 

 

 

32.

Для данной матрицы А, Х(λ)=det(A-λE), где Е — единичная матрица, является многочленом от λ, который называется характеристическим многочленом матрицы A. Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение Aϑ=λϑ имеет не нулевое решение, то (A- λE) ϑ=0, значит матрица A-λE вырождена и ее определитель det(A-λE)= Х(λ) равен нулю.
Характеристический многочлен линейного оператора не зависит от выбора ба­зиса (одинаков для всех базисов)

 

 

. если линейный оператор, действующий в n-мерном линейном пространстве X, имеет n различных собственных значений, то собственные векторы оператора образуют базис в пространстве X; этот базис называют собственным базисом оператора;

матрица оператора в базисе из его собственных векторов имеет диагональную форму с собственными значениями на диагонали.

 

 

34.

Квадратичная форма — функция на векторном пространстве, задаваемаяоднородным многочленом второй степени от координат вектора
Ортогональное преобразование. Для того чтобы привести квадратич­ную форму f(x_l,x₂,x₃) к каноническому виду, необходимо выписать матрицу квадратичной формы у которой A _ij = A_ji т. е. элементы, симметричные относительно главной диа­гонали, совпадают. Затем составляем и решаем характеристическое уравне­ние:
Так как матрица симметричная, то корни λ₁,λ₂,λ₃ характеристического уравнения являются действительные числа. Найденные собственные числа являются коэффициентами в каноническом виде квадратичной формы в ба­зисе е'₁,е'₂, е'₃:
f(x'₁,x'₂, x'₃)= f₁x'²₁ + f₂x'²₂ + f₃x'²₃
Пусть найдены нормированные собственные векторы, соответствую­щие характеристическим числам γ ₁ γ ₂, γ₃ в ортонормированном базисе е₁ е₂, е₃:
е'₁ = q₁₁ е₁+ q₂₁ е₂ + q₃₁ е₃ ,
е'₂ = q₁₂ е₁+ q₂₂ е₂ + q₃₂ е₃ ,
е'₃ = q₁₃ е₁+ q₂₃ е₂ + q₃₃ е₃ ,
В свою очередь, векторы е'_ь е'₂, е'з образуют ортонормированный базис. Матрица является матрицей перехода от базиса e₁, е₂, е₃ к базису е'₁,е'₂, е'₃. Формулы преобразования координат при переходе к новому ортонор-мированному базису имеют вид: Принято говорить, что квадратичная форма f(x_l,x₂,x₃) приведена к каноническому виду с помощью ортогонального преобразования В.

 

35 мнимый эллипс х²/а² + у²/в² = -1
эллипс х²/а² + у²/в² = 1 а=в окружность
гипербола х²/а² - у²/в² = 1 а,в-полуоси гиперболы
а=в равнобокая гипербола
у=±(в/а)х – асимптоты

Мнимые пересекающиеся прямые х²/а² + у²/в² = 0
Пара действительных прямых х²/а² - у²/в² = 0
Парабола у²=2рх р-факальный параметр
Пара мнимых параллельных прямых х²+а²=0
пара действительных параллельных прямых х²-а²=0

 

 

36 Эллипсоид х²/а² + у²/в² + z²/c² = 1 а,в,с- полуоси
а=в а=с с=в эллипсоид вращения
а=в=с-сфера
Однополосный гиперболоид х²/а² + у²/в² - z²/c² = 1
а=в гиперболоид вращения по оси z
Двуполостный гиперболоид х²/а² + у²/в² - z²/c² = -1
Конус х²/а² + у²/в² - z²/c² = 0
Эллиптический параболоид z= х²/а² + у²/в²
Гиперболический параболоид z= х²/а² - у²/в²
Эллиптический цилиндр х²/а² + у²/в² =1
Гиперболический цилиндр х²/а² - у²/в² =1
Параболический цилиндр у²=2рх