| Маятники | Свободное состояние | Начальное отклонение | Возвращение в равновесие | Противоположное отклонение | Возвращение в равновесие | Исходное состояние | ||||||
| Пружинный F упр = – kx |
 0 1 2 3 4 1
| |||||||||||
| х = 0 Е = 0 | х = х0 Еn = max V = 0 Ек = 0 | x = 0 Еn = 0 V = max Ек = max | х = х0 Еn = max V = 0 Ек = 0 | x = 0 Еn = 0 V = max Ек = max | х = х0 Еn = max V = 0 Ек = 0 | |||||||
| Математический |
 0
α = 0 Е = 0
положение
равновесия
| α = α0 Еn= max V = 0 Ек = 0 | α = 0 Еn = 0 V = max Eк = max | α = α0 Еn = max V = 0 Ек = 0 | α = 0 Еn= 0 V = max Eк = max | α = α0 Еn = max V = 0 Е к = 0 | ||||||
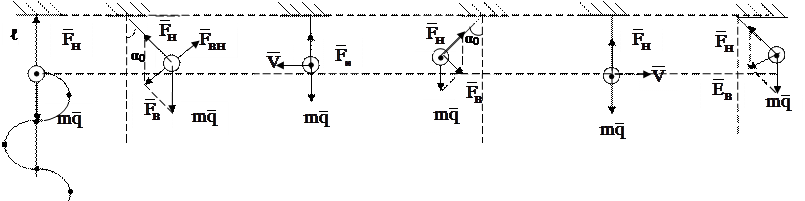
| Электромагнитный контур |
q = 0 W = 0
|
q = q0 Wэ = max
J = 0 Wм = 0
J >> εsi < 0
начальная
зарядка
|
 2
q = 0 Wэ = 0
J = max Wм = max
J << εsi > 0
J >> εsi > 0
разрядка
|
q = 0 Wэ = max J = 0 Wм = 0 J >> εsi < 0 перезарядка
|
 4
q = 0 Wэ = 0
J = max Wм = max
J << εsi > 0
разрядка
|
q = q0 Wэ = max
J = 0 Wм = 0
исходная
зарядка
| ||||||
Расчёт частоты и периода незатухающих колебаний для пружинного, физического,
Математического маятников и колебательного контура
| Маятник | Пружинный | Физический | Математический | Колебательный контур | |
| Основной параметр | 
| 
| 
| 
| |
| х – смещение (м) | α – угловое смещение (рад) | q – электрический заряд (Кл) |
| Окончание таблицы | |||||
| Основной закон | Второй закон Ньютона для поступательного движения
| Второй закон Ньютона для вращательного движения
| Правило Кирхгофа для контура
| ||
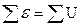
| 3. Силы (ЭДС) | F= – k x | M = – mgℓ . sin α | Uc= εsi = – 
Uc = 
| ||
| 4.Ускорение | a = x|| | a= x|| | 
| ||
| Дифференциальное уравнение 5. ДУ І | 
| 
| 
| ||
| 6. ДУ ІІ | 
| 
| 
| ||
| 7. Частота незатухающих колебаний | 
| 
| J= mℓ2 
| 
| |
| 8.Период незатухающих колебаний | 
| 
| 
| 
| |
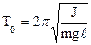
| 9. Коэффициент затухания | σ = 0 | σ = 0 | σ = 0 | σ = 0 | |
| 10. Решение ДУ | 
| 
| 
| 
| |
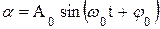
| 11. Амплитуда | А0 = const | А0 = const | А0 = const | А0 = const | |
| 12. Особенности | 
Тфм = Тмм 
|
Сравнение незатухающих и затухающих механических и электромагнитных колебаний
| Механические колебания пружинного маятника | Электромагнитные колебания в контуре | ||||
| Основной параметр | х – смещение | q – электрический заряд | |||
| Основной закон | F = ma | 
| |||
| Сила (Э.Д.С.) | незатухающие | затухающие | незатухающие | затухающие | |
| F = F упр = – k х | F=F упр+Fсопр= – k х–rV | 
| 
| ||
| Ускорение | а = х|| | V = х| а = V| = х|| | 
| J = 
| |
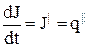
| Дифференциальное уравнение ДУ І | 
| 
| 
| 
| |
| ДУ ІІ | 
| 
| 
| 
| |
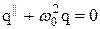
| Циклическая Частота | 
| 
| 
| 
| |
| Окончание таблицы | |||||
| Период | 
| 
| 
|
| |
| Коэффициент затухания | σ = 0 | 
| σ = 0 | 
| |
| Решение ДУ |
| 
| 
| 
| |
| Амплитуда | А0 = const | 
| А0 = const |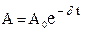 
| |
| Особенности | 
| 
| |||
| Графики | а) | б) |
Графики механического колебания пружинного маятника
 |
а) незатухающий б) затухающий
Сравнение свободных и вынужденных электромагнитных колебаний
| Колебательный контур | Свободные колебания | Вынужденные колебания | |||
| Незатухающие | затухающие |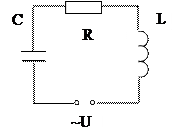 
| |||
| 
| ||||
| Внешний источник | нет | нет | Переменная ЭДС | ||
| Дифференциальные уравнения ДУ І ДУ ІІ | 
|
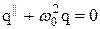
| U= Um. sin (ωвt)
| ||
| периодические | апериодические | ||||
| Сопротивление | R ≈0 | R < R кр | R ≥ R кр | R – любое | |
| Циклическая частота | 
|  (δ<<)
|  (δ>>)
| 
| |
| Особенность | 
| ||||
| Период | 
| 
|   0
 Т ∞
| 
| |
| Решение ДУ | 
| 
| q =Aз | 
| |
| Амплитуда | А0 = const | 
| 
| ||
| График | а) | б) | в) | г) | |
| Окончание таблицы |
10. График
а) б) в)
г)
Сравнение трёх элементов цепей переменного тока
| Резистор | Катушка | Конденсатор | |
| Обозначение на схеме | 
| 
| 
|
| Параметр | Сопротивление | Индуктивность | Ёмкость |
| Сопротивление | R – активное | ХL – реактивное индуктивное | ХС – реактивное ёмкостное |
| Зависимость сопротивления от частоты | Не зависит R = const | прямопропорционально ХL = ωt | обратно прямопропорционально
|
| Для постоянного тока (ω = 0) | R = const | ХL → 0 | ХС → ∞ |
| Векторная диаграмма | 
| 
| 
|
| Направление вектора тока | Совпадает по фазе с вектором напряжения | отстаёт от вектора напряжения на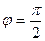 
| опережает от вектора напряжения на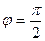
|