Лабораторная работа «Алгоритмы и блок-схемы»

1. Используя материалы лекции по теме, выполните на доске задания из файла Primery_Blok-skhem.doc

2. В соответствии с номером по журналу выполните задания своего варианта, используя MS WORD. Решите предложенные задачи и представьте алгоритм в виде блок-схемы. Укажите основную базовую алгоритмическую конструкцию для каждой задачи

3. Результат сохраните в файле Отчет_Лабораторная работа_Блок-схемы. Данные представьте по образцу: титульный лист, далее каждая задача на отдельном листе – условие, блок-схема. Пример титульного листа в Приложение 1 в данной лабораторной работе

 

 

Вариант 1

1. Даны числа a₁, b₁, c₁, a₂, b₂, c₂. Вывести координаты точки пересечения прямых, описываемых уравнениями a₁x + b₁y = c₁ и a₂x + b₂y = c₂, либо сообщить, что эти прямые совпадают, параллельны или вовсе не существуют

2. Сколько кругов заданного радиуса r можно вырезать из правильного треугольника со стороной а?

3. Составить алгоритм решения ребуса КОТ + КОТ = ТОК (различные буквы обозначают различные цифры, старшая — не 0).

4. Написать программу, которая бы по введённому номеру единицы измерения (1 – дециметр, 2 – километр, 3 – метр, 4 – миллиметр, 5 – сантиметр) и длине отрезка L выдавала бы соответствующее значение длины отрезка в метрах.

5. Найти 10 первых натуральных чисел, оканчивающихся на цифру 7, кратных числу 9 и больших 100.

 

Вариант 2

1. Введите количество посадочных мест. Напечатайте соответствующий этому количеству вид транспорта: «велосипед», «мотоцикл», «легковой автомобиль», «микроавтобус», «автобус».

2. Определить, принадлежит ли точка M (x, y) кольцу с центром в начале координат, внешним радиусом R₁, и внутренним радиусом R₂ (R₁ > R₂).

3. Составить алгоритм решения ребуса ДРУГ – ГУРД = 2727 (различные буквы обозначают различные цифры, старшая — не 0).

4. Животновод в начале каждой зимы повышает отпускную цену на молоко на p%, а каждым летом – снижает на столько же процентов. Изменится ли цена на молоко и если да, то в какую сторону и на сколько через n лет?

5. Дано натуральное число. Выяснить, является ли оно простым.

 

Вариант 3

1. Определить методом половинного деления корень уравнения на промежутке [1;2] с точностью 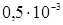. Оценить число итераций для достижения заданной точности.

2. Выяснить, принадлежит ли точка M (x, y) кругу радиуса r с центром в точке с координатами a, b.

3. Владелец автомобиля приобрел новый карбюратор, который экономит 50% топлива, новую систему зажигания, которая экономит 30% топлива, и поршневые кольца, экономящие 20% топлива. Верно ли, что его автомобиль теперь сможет обходиться совсем без топлива? Найти фактическую экономию для произвольно заданных сэкономленных процентов.

4. Составить алгоритм решения ребуса МУХА + МУХА + МУХА = СЛОН (различные буквы обозначают различные цифры, старшая — не 0).

5. Введите время суток (только часы). Напечатайте соответствующее этому времени сообщение: «Доброе утро», «Добрый день», «Добрый вечер», «Доброй ночи».

 

Вариант 4

1. Определить и вывести на печать номер квадранта, в котором расположена точка M (x, y). Если точка лежит на оси, выдать об этом сообщение.

2. У квадрата ABCD на плоскости известны координаты двух противоположных вершин – точек А и С. Найти координаты точек B и D. Расположение квадрата произвольно; его стороны не обязательно параллельны координатным осям.

3. Составить алгоритм решения ребуса РАДАР = (Р + А + Д)⁴ (различные буквы обозначают различные цифры, старшая — не 0).

4. Определить методом половинного деления корень уравнения на промежутке [–1;0] с точностью .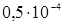

5. С начала 1990 года по некоторый день прошло n месяцев и 2 дня (n ≥ 1). Определить, к какому месяцу (январь, февраль и т. д.) относится этот день

 

Вариант 5

1. Суточный рацион коровы составляет u кг сена, v кг силоса и w кг комбикорма. В хозяйстве, содержащем стадо из k голов, осталось s центнеров сена, t тонн силоса и f мешков комбикорма по 50 кг. Сколько еще дней хозяйство сможет кормить коров по полному рациону? Какой из кормов кончится раньше других?

2. Напечатать в возрастающем порядке все трехзначные числа, в десятичной записи которых нет одинаковых цифр (операции деления и нахождения остатка от деления не использовать).

3. Все клетки шахматной доски пронумерованы от 1 до 64 так, что первая строка клеток имеет номера от 1 до 8, вторая – от 9 до 16 и т. д. Написать программу, которая на ввод номера клетки выводит номера всех клеток, имеющих с ней общую сторону.

4. Используя метод итераций, вычислить значение функции 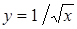по итерационной формуле 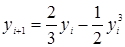cточностью .

5. Дано трехзначное число. Определить четырехзначное число, полученное приписыванием цифры единиц в качестве цифры тысяч (например, из числа 137 необходимо получить число 7137).

 

Вариант 6

1. На ввод в программу натурального числа, не превышающего миллион, программа выводит словами на русском языке введенное число и слово «учеников». Например, на ввод числа 21 385 программа выводит «двадцать одна тыся­ча триста восемьдесят пять учеников».

2. Может ли шар радиуса r пройти через ромбообразное отверстие с диагоналями p и q?

3. Найти наименьший номер элемента последователь­ности, для которого выполняется условие М. Вывести на экран этот номер и все элементы a_i, где i = 1, 2,..., п, .

4. Вычислить количество точек с целочисленными координа­тами, находящихся в круге радиуса R (R > 0).

5. Два поезда идут навстречу друг другу со скоростями 36 и 54 км/ч. Пассажир, находящийся в первом поезде, замечет, что второй проходит мимо него в течение 6 секунд. Какова длина второго поезда?

 

Вариант 7

1. Составить программу, которая находит наибольшее значе­ние отношения n -значного числа к сумме его цифр (1 £ n £ 59).

2. Пуля, летящая со скоростью 400 м/с, ударяется в земной вал и проникает в него на глубину 36 см. Сколько времени двигалась она внутри вала? С каким ускорением? Какова была ее скорость на глубине 18 см? На какой глубине скорость пули уменьшилась в 3 раза? Движение считать равноускоренным.

3. В некотором учебном заведении действуют следующие правила приема. Абитуриенты сдают три экзамена. Если они набирают не менее 13 баллов, то это дает право поступить на дневное отделение, от 10 до 12 – на вечернее, от 8 до 9 – на заочное; ниже 8 баллов означает отказ в приеме на учебу. Написать программу, которая в зависимости от суммы набранных баллов сообщает абитуриенту его права на поступление.

4. По четырехзначному номеру года, запрошенному с клавиатуры определите номер столетия (например, для 1492 г. – ответ XV век, для 1812 г. – XIX век). Учесть, что началом века считается первый, а не нулевой, год. (То есть, 2000-й год – последний год XX века).

5. В водоеме 100 т рыбы. Каждый год рыболовецкая бригада вылавливает 15т. Воспроизводство рыбы 5% в год. Для сохранения воспроизводства необходимо прекращать лов, когда в водоеме ее остается менее 5 т. Через сколько лет лов рыбы должен быть прекращен?

 

Вариант 8

1. Идет k -я секунда суток. Определить, сколько полных часов и полных минут прошло к этому моменту.

2. Найти произведение цифр заданного k -значного числа.

3. Найти координаты точек пересечения прямой y = kx + b и окружности радиуса R c центром начале координат. В каких координатных четвертях находятся точки пересечения? Если точек пересечения нет или прямая касается окружности, выдать соответствующее сообщение.

4. Подрабатывая вечерами курьером, школьник решил накопить сумму в S рублей для покупки компьютера. В пер­вый месяц он отложил Р рублей. Затем его вклад каждый раз был на 5% больше предыдущего вклада. Через сколько месяцев школьник сможет купить компьютер? Величины Р и S задавать вводом с клавиатуры.

5. Ежемесячная стипендия студента составляет А руб., а рас­ходы на проживание превышают стипендию и составляют В руб. в месяц. Рост цен ежемесячно увеличивает расходы на 3%. Составьте программу расчета суммы денег, которую необходимо единовременно попросить у родителей, чтобы можно было прожить учебный год (10 месяцев), используя только эти деньги и стипендию.

 

Вариант 9

1. Составить программу для определения подходящего возраста кандидатуры для вступления в брак, используя следующее соображение: возраст девушки равен половине возраста мужчины плюс 7, возраст мужчины определяется соответственно как удвоенный возраст девушки минус 14.

2. Сколько чисел последовательности 2, 4, 6, 8,... нужно взять, чтобы их сумма превысила 1000? Вывести величи­ну последнего слагаемого и суммы.

3. Покупатель должен заплатить в кассу N руб. У него имеются купюры по 1, 5, 10, 50, 100, 500, 1000 и 10000 руб. Сколько купюр разного достоинства отдаст покупатель, если он начинает платить с самых крупных купюр?

4. Если сумма трех попарно различных вещественных чисел X, Y, Z меньше единицы, то наименьшее из этих трех чисел заменить полусуммой двух других; в противном случае заменить меньшее из X, Y, полусуммой двух оставшихся.

5. Документ содержит текст из 32 строк по 60 символов в каждой и точечную черно-белую фотографию 10 ´ 15 см. Каждый квадратный сантиметр содержит 300 точек, любая точка описывается 4-мя битами. Каков общий информационный объем документа в Кбайтах?

 

Вариант 10

1. Пусть элементами равностороннего треугольника являются: сторона а; площадь S; высота h; радиус вписанной окружности r; радиус описанной окружности R. Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.

2. Расстояние до ближайшей к Земле звезды Альфа Центавра 4,3 световых года. Скорость света принять 300000 км/с. Скорость земного звездолета 100 км/с. За сколько лет звездолет долетит до звезды?

3. Около стены наклонно стоит палка длиной х м. Один ее конец находится на расстоянии у м от стены. Определить значение угла a между палкой и полом для значений х = k м и у, изменяющегося от 2 до 3 м с шагом h м.

4. Известен факториал числа п. Найти это число (факториал числа п равен 1×2×...× п).

5. Работа светофора для пешеходов запрограммирована следующим образом: в начале каждого часа в течение трех минут горит зеленый сигнал, затем в течение двух минут – красный, в течение трех минут – опять зеленый и т.д. Дано вещественное число t, означающее время в минутах, прошедшее с начала очередного часа. Определить, сигнал какого цвета горит для пешеходов в этот момент.

 

Вариант 11

1. Имеются стол прямоугольной формы с размерами a × b (a и b – целые числа, a > b) и кости домино с размерами c ´ d ´ e – целые числа, c > d > e). Найти вариант размещения на столе наибольшего количества костей. Все размещаемые кости должны лежать на одной и той же грани в один ярус и не свешиваться со стола. Все ребра костей домино должны быть параллельны или перпендикулярны каждой стороне стола.

2. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы пре­дыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?

3. Написать программу, которая бы по введенному номеру единицы измерения (1 – килограмм, 2 – миллиграмм, 3 – грамм, 4 – тонна, 5 – центнер) и массе М выдавала бы соответствующее значение массы в килограммах.

4. Определить: а) является ли заданное число степенью числа 3;

б) является ли заданное число степенью числа 5.

5. Представить комплексное число А + Bi (А, В – вещественные) в тригонометрическом виде.

 

Вариант 12

1. В подъезде жилого дома имеется n квартир, пронумерованных подряд, начиная с номера а. Определить, является ли сумма номеров всех квартир четным числом. Формулу суммы членов арифметической прогрессии не использовать

2. Окружность вписана в квадрат заданной площади. Найти площадь квадрата, вписанного в эту окружность. Во сколько раз площадь вписанного квадрата меньше площади заданного?

3. Даны два действительных положительных числа х и у. Арифметические действия над числами пронумерованы (1 – сложение, 2 – вычитание, 3 – умножение, 4 – деление). Составить программу, которая по введенному номеру выполняет то или иное действие над числами.

4. Дано число a (1 < a £ 1,5). Найти такое наименьшее n, что в последовательности чисел 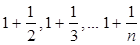последнее число будет меньше a.

5. Имеется серия измерений элементов треугольника. Группы элементов пронумерованы. В серии в произвольном порядке могут встречаться такие группы элементов треугольника:1) основание и высота; 2) две стороны и угол между ними (угол задан в радианах); 3) три стороны. Разработать программу, которая запрашивает номер груп­пы элементов, вводит соответствующие элементы и вычисляет площадь треугольника. Вычисления прекратить, если в качестве номера группы введен 0.

 

Вариант 13

1. Даны вещественные положительные числа a, b, c, d. Выяснить, можно ли прямоугольник со сторонами a, b уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.

2. Найти частное произведений четных и нечетных цифр четырехзначного числа.

3. Составить программу, которая для любого натурального числа печатает количество цифр в записи этого числа.

4. Написать программу решения уравнения 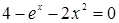(x > 0) с точностью до сотых методом половинного деления.

5. У гусей и кроликов вместе 2n лап. Сколько может быть гусей и кроликов (вывести все возможные сочетания)?

 

Вариант 14

1. Вычислить число и месяц в невисокосном году по номеру дня.

2. Полторы кошки за полтора часа съедают полторы мышки. Сколько мышек съедят X кошек за Y часов?

3. Фирма ежегодно на протяжении n лет закупала оборудование стоимостью соответственно s₁, s₂,…, s_n pуб. в год (эти числа вводятся и обрабатываются последовательно). Ежегодно в результате износа и морального старения (амортизация) все имеющееся оборудование уценяется на p%. Какова общая стоимость накопленного оборудования за n лет?

4. Установить закономерности образования следующего ряда: 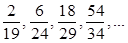и найти их сумму с точностью x.

5. Написать программу, которая по введенному числу от 1 до 12 (номеру месяца) выдает все приходящиеся на этот месяц праздничные дни (например, если введено число 1, то должно получиться 1 января – Новый год, 7 января – Рождество).

Вариант 15

1. Написать программу, которая по вводимому числу от 1 до 11 (номеру класса) выдает соответствующее сообщение «Привет, k -классник». Например, если k = 1, «Привет, первоклассник»; если k = 4, «Привет, четвероклассник».

2. Написать программу, которая по паролю определяет уровень доступа сотрудника к секретной информации в базе данных. Доступ к базе имеют только шесть человек, разбитых на три группы по уровням доступа. Они имеют следующие пароли: 9583, 1747 – доступны модули баз A, B, C; 3331, 7922 – доступны модули баз B, C; 9455, 8997 – доступен модуль базы C.

3. Числа вводятся с клавиатуры до первого отрицательно­го числа. Написать программу, которая находит номера начала и конца наиболее длинной последовательности нулей.

4. Известно время начала и окончания (например, 6:00 и 24:00) работы некоторого пригородного автобусного маршрута с одним автобусом на линии, а также протяженность маршрута в минутах (в один конец) и время отдыха на конечных остановках. Составить суточное расписание этого маршрута (моменты отправления и конечных пунктов) без учета времени на обед и пересменку.

5. Составить программу для вычисления пути, пройденного лодкой, если ее скорость в стоячей воде v км/ч, скорость течения реки v₁ км/ч, время движения по озеру t₁ ч, а против течения реки – t₂ ч.

 

Вариант 16

1. В небоскребе N этажей и всего один подъезд; на каждом этаже по 3 квартиры; лифт может останавливаться только на нечетных этажах. Человек садится в лифт и набирает номер нужной ему квартиры M. На какой этаж лифт должен доставить пассажира?

2. Дано значение a. Не используя, никаких операций, кроме умножения, получить значение а⁸ за три операции и а¹⁰ за четыре операции.

3. Каждая из деталей должна последовательно пройти обработку на каждом из трёх станков. Продолжительность обработки каждой детали на каждом станке вводится группами по 3 числа, до исчерпания ввода. Сколько времени займет обработка всех деталей?

4. Написать программу, которая бы по введенному номеру единицы измерения (1 – дециметр, 2 – километр, 3 – метр, 4 – миллиметр, 5 – сантиметр) и длине отрезка L выдавала бы соответствующее значение длины отрезка в метрах.

5. Числа вводятся с клавиатуры до тех пор, пока не встре­тятся идущие подряд три отрицательных числа. Написать прог­рамму, печатающую те тройки чисел, которые могут быть длина­ми сторон равнобедренного треугольника.

Вариант 17

1. Для целого числа k с от 1 до 99 напечатать фразу «Мне k лет», учитывая при этом, что при некоторых значениях k слово «лет» надо заменить на слово «год» или «года». Например, 11 лет, 22 года, 51 год.

2. Написать алгоритм, определяющий сумму цифр в заданном натуральном трехзначном числе. Например, для 139 ответом будет 13.

3. Заданы три положительных числа a, b, и с. Определить, являются ли они последовательно стоящими элементами арифметической или геометрической прогрессии. Если являются, то вычислить разность или знаменатель прогрессии.

4. Даны числовой ряд и некоторое число x. Найти сум­му тех членов ряда, модуль которых больше или равен x. Общий член ряда имеет вид: .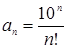

5. Предприниматель, начав дело, взял кредит размером R рублей под p процентов годовых и вложил его в своё дело. По прогнозам, его дело должно давать прибыль r рублей в год. Сможет ли он накопить сумму, достаточную для погашения кредита, и если да, то через сколько лет?

 

Вариант 18

1. Написать программу, определяющую вид заданного треугольника (равнобедренный, равносторонний или разносторонний) по длинам сторон.

2. Написать алгоритм, определяющий третью цифру дробной части заданного вещественного числа. Например, для 0.16453 ответом будет цифра 4.

3. Числа вводятся с клавиатуры, пока не встретится число 0. Написать программу, проверяющую, для всех ли чисел выпол­няется условие «Разность между двумя соседними числа­ми не больше 36,65 ».

4. Для заданного многозначного натурального числа находится сумма цифр. Если полученная сумма не однозначное число, то вновь находится сумма цифр для найденной суммы. Операция выполняется до тех пор, пока не будет получено одноз­начное число. Найти это число.

5. В старояпонском календаре был принят 12-летний цикл. Годы внутри цикла носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. Написать программу, которая вводит номер некоторого года и печатает его название по старояпонскому календарю. (Справка: 1996 г. – год Крысы – начало очередного цикла.)

 

Вариант 19

1. Написать программу, проверяющую, можно ли построить треугольник, длины сторон которого равны трем заданным числам

2. Написать алгоритм, определяющий цифру сотен в заданном натуральном числе. Например, для 13905 ответом будет цифра 9.

3. Ежедневная выручка лавочника равна половине выруч­ки предыдущего дня минус 1/4 выручки второго предыдущего дня плюс 0,15 выручки третьего предыдущего дня. Написать программу, определяющую, через сколько лет разбогатеет лавоч­ник (по его мнению, богатым человеком можно считать того, у кого имеется 1000 долл.), если выручка первых трех дней соста­вила по 1 долл. в день.

4. Царевна-лягушка съедает ежедневно на 20% комаров больше, чем в предыдущий день, и еще два комара. Написать программу, определяющую, через сколько дней количество съеденных комаров превысит 100, если в первый день было съедено 12 комаров.

5. Написать программу, которая бы по введенному номеру времени года (1 – зима, 2 – весна, 3 – лето, 4 – осень) выдавала соответствующие этому времени года месяцы и сумму дней сезона.

 

Вариант 20

1. Написать программу, проверяющую истинность высказывания «Сумма двух первых цифр четырехзначного числа равна сумме двух последних».

2. Написать алгоритм, определяющий, на какую цифру оканчивается заданное натуральное число.

3. Ежедневно Незнайка учит половину иностранных слов от суммы выученных за два предыдущих дня и еще два слова. Знайка считает, что силы Незнайки иссякнут, когда нужно будет выучить 50 слов в день. Написать программу, определяющую, через сколько дней иссякнут силы у Незнайки, если в первые два дня он выучил по одному слову.

4. Пусть элементами прямоугольного равнобедренного треугольника являются: катет а; гипотенуза b; высота h, опущенная из вершины прямого угла на гипотенузу; площадь S. Составить программу, которая по заданному номеру и значению соответствующего элемента вычисляла бы значение всех остальных элементов треугольника.

5. Любое натуральное число можно единственным образом разложить на произведение степени двойки и нечетного чис­ла. Написать программу, производящую такое разложение для произвольного натурального числа.

 

Вариант 21

1. Написать программу, проверяющую истинность высказывания «Среди цифр заданного трехзначного числа есть одинаковые».

2. Вычислить, используя не более восьми операций умножения и восьми операций сложения или вычитания:

.

3. На каждом следующем дне рождения Винни-Пух съедает столько же пищи, сколько на двух предыдущих. На двух первых днях рождения у Пятачка и Кролика он съел по 100 г пищи. Написать программу, определяющую, на каком дне рождения вес съеденной пищи превысит собственный вес Винни-Пуха.

4. С клавиатуры вводится строго возрастающая последо­вательность натуральных чисел до тех пор, пока произведение трех соседних введенных чисел не превысит 100. Вычислить сумму факториалов всех введенных чисел. Эта работа должна быть выполнена как можно эффективнее, без повторов.

5. Пусть элементами круга являются радиус (первый элемент), диаметр (второй элемент) и длина окружности (третий элемент). Составить программу, которая по номеру элемента запрашивала бы его соответствующее значение и вычисляла бы площадь круга.

 

Вариант 22

1. Написать программу, проверяющую истинность высказывания «Цифра пять входит в десятичную запись четырехзначного числа k».

2. Вычислить значения двух многочленов, используя не более 11 операци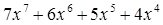й:

и .

3. Составить программу, позволяющую получить словесное описание школьных отметок (1 – «плохо», 2 – «неудовлетворительно», 3 – «удовлетворительно», 4 – «хорошо», 5 – «отлично»).

4. Числа вводятся с клавиатуры до тех пор, пока не будет введен нуль. Обозначим: x_i – число, введенное i -м, х_n – число, введенное последним (перед нулем). Написать программу для вычисления выражения (без использования массива)

.

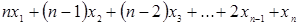5. Спортсмен, начав тренировки, в первый день пробежал 10 км. Каждый следующий день он увеличивал дистанцию на 12%. Написать программу, определяющую общую длину пробега за месяц и первый день с начала тренировок, после которого дистанция превысит 25 км.

 

Вариант 23

1. Написать программу, проверяющую истинность высказывания «Одно из четырех чисел отлично от других, равных между собой».

2. Вычислить, используя не более четырех операций умножения и четырех операций сложения или вычитания: .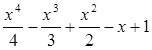

3. Агент по продаже автомобилей стоимостью А руб. продал первый автомобиль за В руб. Каждый следующий автомобиль он продавал на 40% дороже предыдущего. Написать программу, вычисляющую прибыль агента за продажу N автомобилей и определяющую, после продажи ка­кого автомобиля прибыль превысит стоимость автомобиля в два раза.

4. Найти наименьший номер члена последовательности, для которого выполняется условие 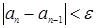. Вывести на экран этот номер и все элементы а_i,где i = 1, 2 ..... п: .

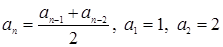5. Составить программу, которая по данному числу (1 – 12) выводит название соответствующего ему месяца и определяет количество дней заданного месяца в текущем году.

Вариант 24

1. Заданы координаты точки x и у. Определить ее расположение в декартовой прямоугольной системе координат.

2. Вычислить, используя не более четырех операций умножения и четырех операций сложения или вычитания: .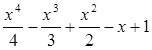

3. Для каждой введенной цифры (0 – 9) вывести соответствующее ей название на английском языке (0 – zero, 1 – one, 2 – two,...).

4. Числа вводятся с клавиатуры до тех пор, пока не будет введен нуль. Обозначим: x_i – число, введенное i -м, х_n – число, введенное последним (перед нулем). Написать программу для вычисления выражения (без использования массива)

.

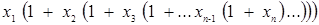5. Коммерсант ежемесячно увеличивает на z % и еще на 5 руб. цену туфель, первоначальная цена которых X руб. Написать программу, определяющую, через сколько месяцев цена туфель будет превышать Y руб. и какую прибыль за это время получит коммерсант, если инфляция составляет Q % в месяц.

 

Вариант 25

1. Написать программу нахождения всех целых положительных чисел, не превосходящих N, которые имеют ровно M целых положительных делителей.

2. Представить в виде алгоритма решение задачи. Имеются три сосуда емкостью 8, 5 и 3 л. Первый из них наполнен водой. Как разлить воду в два из этих сосудов так, чтобы в каждом было по 4 л?

3. Составить программу, которая по заданным году и номеру месяца m определяет количество дней в этом месяце.

4. Богатый дядюшка подарил мне 1 доллар в мой первый день рождения. В каждый следующий день рождения он удваивал сумму подарка и прибавлял к ней столько долларов, сколько лет мне исполнилось. Написать программу, подсчитывающую об­щую сумму денег, подаренных к N -му дню рождения, и указывающую, к какому дню рождения сумма подарка превысит 100 долларов.

5. Шахматная доска содержит 8 × 8 клеток. Горизонтали и вертикали обозначаются цифрами 1 – 8. Написать программу, проверяющую, что заданные две клетки имеют одинаковый цвет.

 

Вариант 26

1. Представить в виде алгоритма решение задачи. Имеются две линейки. На одной отмечен отрезок длиной 7 см, а на другой – 5 см. Как, пользуясь для измерений только данными линейками, нанести на них сантиметровые деления?

2. Написать программу, позволяющую по последней цифре числа определить последнюю цифру его квадрата.

3. Шахматная доска содержит 8 × 8 клеток. Горизонтали и вертикали обозначаются цифрами 1 – 8. Написать программу, проверяющую, что заданные две клетки лежат на одной диагонали.

4. Задана последовательность цифр. Можно ли найти в ней две пары стоящих рядом цифр так, чтобы их разность давала число, кратное трем?

5. Три года назад за покупку на базаре 1 кг картофеля, 1 л молока и одного десятка яиц уплачено А руб. С тех пор ежемесячно цена картошки увеличивалась на 30%, цена молока – на 40%, яиц – в два раза. Написать программу ежемесячного изменения стоимости покупки, определяющую, через сколько месяцев цена покупки увеличится более чем вдвое.

 

Вариант 27

1. Любое рациональное число представляется в виде бесконечной десятичной периодической дроби. Написать программу, определяющую период дроби n / m, где n и m – натуральные числа.

2. До школы можно доехать на автобусе, на троллейбусе с пересадкой на трамвай, на такси, дойти пешком с пересадкой на метро. Указать, сколько битов информации приносит сообщение по радио о том, что сегодня троллейбусы не ходят.

3. Задана последовательность цифр десятичной системы счисления. Проверить, можно ли выбрать из цифр этой последовательности две пары расположенных рядом цифр так, чтобы полученные два двухзначных числа образовывали в сумме 100.

4. Написать программу, которая по номеру дня недели (целому числу от 1 до 7) выдает в качестве результата количество уроков в вашем классе в этот день и сколько времени вы провели в школе.

5. До школы можно доехать на автобусе, на троллейбусе с пересадкой на трамвай, на такси, дойти пешком с пересадкой на метро. Указать, сколько битов информации приносит сообщение по радио о том, что сегодня троллейбусы не ходят.

 

Вариант 28

1. Написать программу, которая вводит две даты в формате «дд. мм. гг» и выводит старшую дату.

2. Сколько различных имен длиной не более 5 можно образовать в алгоритмическом языке, используя только следующие символы: a, b, 1, 5, #. Записать решение в виде линейного алгоритма Составить программу, которая бы по двум углам определяла тип треугольника: прямоугольный, остроугольный, тупоугольный, равнобедренный, равносторонний. Причем первые три типа могут сочетаться с двумя последними. Контролировать правильность вводимых значений.

3. Написать программу, проверяющую, достаточно ли 100 слагаемых, чтобы сумма 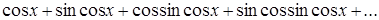превысила заданное А.

4. Сформировать последовательность, состоящую не менее чем из n цифр, такую, что каждое двузначное число, записываемое двумя соседними цифрами (в том порядке, в каком они написаны), должно делиться на 19 или 23. Последовательность должна начинаться на заданную цифру.

 

Вариант 29

1. Написать программу, вычисляющую сумму 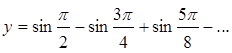. Сумма должна содержать 100 слагаемых, попадающих в промежутке [ a,b ].

2. Сколько четырехзначных нечетных чисел можно образовать, используя цифры: 0, 1, 4, 5, 6, 8? Выписать наименьшее и наибольшее из этих чисел. Записать решение в виде линейного алгоритма.

3. Составить программу, определяющую является ли введенный шестизначный номер «счастливым» (совпадает ли у него сумма трех начальных и трех конечных цифр). Для выделения отдельных цифр во введенном номере можно использовать операции mod и div.

4. Через прямоугольное окошко размером Р × Q Винни-Пух хочет выбросить круглый воздушный шарик радиусом R. Написать программу, определяющую, пройдет ли шарик в окошко.

5. Некто взял ссуду в банке величиной А руб. под В% годовых. Ежегодно заемщик вносит платежи в счет ссуды в С руб. Написать программу, определяющую, через сколько лет будет погашена ссуда, и сумму денег, выплаченных заемщиком банку.

 

Вариант 30

1. Татьяна Ларина, читая очередной французский роман, подсчитала сумму номеров прочитанных страниц. Написать программу, определяющую номер последней прочитанной страницы.

2. Определить номера подъезда и этажа по номеру квартиры девятиэтажного дома, считая, что на каждом этаже ровно 4 квартиры, а нумерация квартир начинается с первого подъезда?

3. Заданы окружность радиуса R с центром в начале коор­динат и прямая, проходящая через точки А (х; у) и В (х; -у). Написать программу, проверяющую, пересекаются ли окружность и прямая, или они касаются друг друга, или не пересекаются и не касаются. Привести тесты для проверки работоспособности программы.

4. Первое любимое число Незнайки – 1, второе – 5. Каждое следующее число получается как сумма удвоенного предыдущего и предпредыдущего. Так, третье любимое число – 11, а четвертое – 27. Вывести любимые числа Незнайки среди первой тысячи и вычислить их сумму.

5. Составить программу, которая бы в зависимости от введенной даты рождения человека в форме «dd. mm. yyyy» выводила бы на экран комментарий: если целых лет от 1 до 6 – «дитя», от 7 до 16 – «школьник», от 17 до 22 – «студент» от 23 до 60 – «большой человек», от 60 – «отдыхающий».

 

Приложение 1

МИНПРОСВЕЩЕНИЯ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный педагогический университет им. Л.Н. Толстого» (ТГПУ им. Л.Н. Толстого)

 

Кафедра информатики и информационных технологий

 

 

ОТЧЕТ

по дисциплине:

«Введение в программирование»

Лабораторная работа № _

ВАРИАНТ № _

 

 

Выполнил:

студент группы _______________

факультета математики, физики и

информатики

ФИО: _______________________