ЭЛЕКТРОСТАТИКА. ЭЛЕКТРОДИНАМИКА.
ЭЛЕКТРОМАГНЕТИЗМ
ЭЛЕКТРОСТАТИКА
· Закон Кулона:
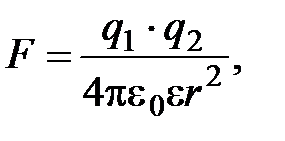
где F - модуль силы взаимодействия двух точечных зарядов величиной q 1 и q2, r - расстояние между зарядами, e - диэлектрическая проницаемость среды, e0 - электрическая постоянная.

· Напряженность электрического поля:
| , |
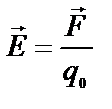
| , |

где 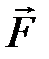 - сила, действующая на точечный заряд q0, помещенный в данную точку поля.
- сила, действующая на точечный заряд q0, помещенный в данную точку поля.
· Напряженность поля точечного заряда (по модулю):

где r - расстояние от заряда q до точки, в которой определяется напряженность.
· Напряженность поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):

где 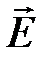 - напряженность в данной точке поля, создаваемого i-тым зарядом.
- напряженность в данной точке поля, создаваемого i-тым зарядом.
· Модуль напряженности поля, создаваемого бесконечной равномерно заряженной плоскостью:
 ,
,
где 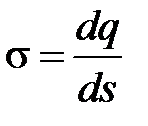 - поверхностная плотность заряда.
- поверхностная плотность заряда.
· Модуль напряженности поля плоского конденсатора в средней его части:
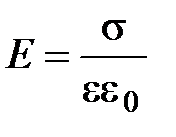 .
.
Формула справедлива, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
· Напряженностьполя, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от нити или оси цилиндра по модулю:
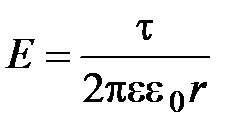 ,
,
где  - линейная плотность заряда.
- линейная плотность заряда.
· Поток вектора напряженности  электрического поля:
электрического поля:
а) через произвольную поверхность, помещенную в неоднородное поле
 ,
,
где a - угол между вектором напряженности 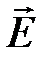 и нормалью
и нормалью 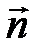 к элементу поверхности, dS - площадь элемента поверхности, En - проекция вектора напряженности на нормаль;
к элементу поверхности, dS - площадь элемента поверхности, En - проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле:
 ,
,
в)через замкнутую поверхность:
 ,
,
где интегрирование ведется по всей поверхности.
Теорема Гаусса. Поток вектора напряженности через любую замкнутую поверхность S равен алгебраической сумме зарядов q1, q2,..., qn, охватываемых этой поверхностью, деленной на e × e0.
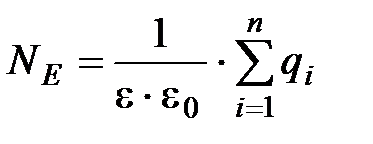 .
.
· Потенциал электрического поля:
j = 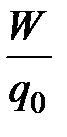 ,
,
где qо - точечный положительный заряд, помещенный в данную точку поля, W - потенциальная энергия заряда qо в данной точке поля.
· Потенциальная энергия системы двух точечных зарядов Q и q:
W =  ,
,
где r - расстояние между зарядами. Потенциальная энергия положительна при взаимодействии одноименных зарядов и отрицательна при взаимодействии разноименных.
· Потенциал электрического поля, созданного точечным зарядом Q на расстоянии r:
j = 
· Потенциал электрического поля, созданного металлической сферой радиуса R, несущей заряд Q:
j =  (r ≤ R; поле внутри и на поверхности сферы),
(r ≤ R; поле внутри и на поверхности сферы),
j = 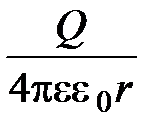 (r > R; поле вне сферы).
(r > R; поле вне сферы).
· Потенциал электрического поля, созданный системой n точечных зарядов:
Согласно принципу суперпозиции электрических полей потенциал электрического поля, созданный системой n точечных зарядов равен алгебраической сумме потенциалов j1, j2,…, jn, создаваемых зарядами q1, q2,..., qn в данной точке поля
j = 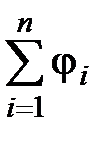 .
.
· Связь потенциалов с напряженностью:
а) в общем случае 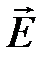 = - qradj или
= - qradj или 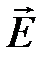 =
= 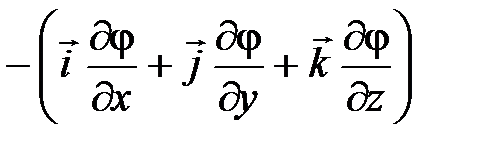 ;
;
б) в случае однородного поля
Е = 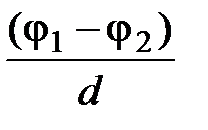 ,
,
где d - расстояние между эквипотенциальными поверхностями с потенциалами j1 и j2 вдоль силовой линии;
в) в случае поля, обладающего центральной или осевой симметрией 
где производная 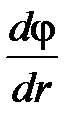 берется вдоль силовой линии.
берется вдоль силовой линии.
· Работа, совершаемая силами поля по перемещению заряда q из точки 1 в точку 2:
A = q (j1 - j2),
где (j1 - j2) - разность потенциалов начальной и конечной точек поля.
· Электроемкость уединенного проводника:
 ,
,
где q - заряд на поверхности проводника, j - потенциал проводника.
· Электроемкость конденсатора:
 ,
,
где (j1 - j2) = U - разность потенциалов (напряжение) между обкладками конденсатора, q - модуль заряда на одной обкладке конденсатора.
· Электроемкость плоского конденсатора в системе СИ:
 ,
,
где S - площадь одной пластины, d - расстояние между обкладками.
· Электроемкость проводящего шара (сферы) в СИ:
с = 4 pee0R,
где R - радиус шара, e - относительная диэлектрическая проницаемость среды, e0 = 8,85×10-12 Ф/м.
· Емкость батареи из n конденсаторов, соединенных последовательно:
 .
.
· Емкость батареи из n конденсаторов, соединенных параллельно:
с =  .
.
Последние две формулы применимы для определения емкости многослойных конденсаторов. Расположение слоев параллельно пластинам соответствует последовательному соединению однослойных конденсаторов; если же границы слоев перпендикулярны пластинам, то, считают, что имеется параллельное соединение однослойных конденсаторов.
Примеры решения задач
Пример 1. Два точечных заряда 9 q и - q закреплены на расстоянии l = 50 см друг от друга. Третий заряд q3 может перемещаться только вдоль прямой, проходящей через заряды. Определить положение заряда q3, при котором он будет находиться в равновесии. При каком знаке заряда q3 равновесие будет устойчивым?
| Дано: q1 = 9q q2 = -q l = 0,5 м | Решение: Заряд q3 находится в равновесии в том случае, если геометрическая сумма сил, действующих на него, равна нулю. Это значит, что на заряд q3 должны действовать две силы, равные по модулю и |
| r -? |
противоположные по направлению. Рассмотрим, на каком из трех участков I, II, III (рис. 1) может быть выполнено это условие. Для определенности будем считать, что заряд q3 – положительный.
На участке I на заряд q3 будут действовать две противоположно направленные силы  и
и  Сила
Сила  , действующая со стороны заряда q1, в любой точке этого участка больше силы
, действующая со стороны заряда q1, в любой точке этого участка больше силы  , действующей
, действующей
I
| + |
| _ |

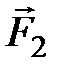 q1 q2
q1 q2
| l |
| q3 |
II
| _ |
| + |
| q3 |

|
 q2
q2
III
| _ |


| q3 |
x
l + x
Рис. 1
со стороны заряда q2, так как больший заряд q1 находится всегда ближе к заряду q3, чем меньший (по модулю) заряд q2. Поэтому равновесие на этом участке невозможно.
На участке II обе силы  и
и  направлены в одну сторону - к заряду q2. Следовательно, и на втором участке равновесие невозможно.
направлены в одну сторону - к заряду q2. Следовательно, и на втором участке равновесие невозможно.
На участке III силы  и
и  направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд q2 всегда находится ближе к заряду q3, чем больший заряд q1. Это значит, что можно найти такую точку на прямой, где силы
направлены в противоположные стороны, так же как и на участке I, но в отличие от него меньший заряд q2 всегда находится ближе к заряду q3, чем больший заряд q1. Это значит, что можно найти такую точку на прямой, где силы  и
и  будут одинаковы по модулю, т. е.
будут одинаковы по модулю, т. е.
 . (1)
. (1)
Пусть х и l + х — расстояние от меньшего и большего зарядов до заряда q3.. Выражая в равенстве (1)  и
и  в соответствии с законом Кулона, получим:
в соответствии с законом Кулона, получим:
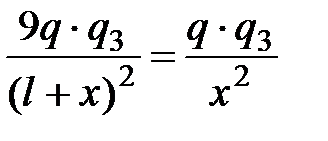 ⟹
⟹  . (2)
. (2)
Решая квадратное уравнение (2) получим два корня:
 .
.
Корень х2 не удовлетворяет физическому условно задачи (в этой точке силы  и
и  хотя и равны по модулю, но направлены в одну сторону).
хотя и равны по модулю, но направлены в одну сторону).
Определим знак заряда q3, при котором равновесие будет устойчивым. Равновесие называется устойчивым, если при смещении заряда от положения равновесия возникают силы, возвращающие его в положение равновесия. Рассмотрим смещение заряда q3 в двух случаях: когда заряд положителен и отрицателен.
Если заряд q3 положителен, то при смещении его влево обе силы  и
и  возрастают. Так как сила
возрастают. Так как сила  возрастает медленнее, то результирующая сила, действующая на заряд q3, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд q3 будет удаляться от положения равновесия. То же происходит и при смещении заряда q3 вправо. Сила
возрастает медленнее, то результирующая сила, действующая на заряд q3, будет направлена в ту же сторону, в которую смещен этот заряд, т. е. влево. Под действием этой силы заряд q3 будет удаляться от положения равновесия. То же происходит и при смещении заряда q3 вправо. Сила  убывает быстрее, чем
убывает быстрее, чем  . Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
. Геометрическая сумма сил в этом случае направлена вправо. Заряд под действием этой силы также будет перемещаться вправо, т. е. удаляться от положения равновесия. Таким образом, в случае положительного заряда равновесие является неустойчивым.
Если заряд q3 отрицателен, то его смещение влево вызовет увеличение сил  и
и  , но сила
, но сила  возрастает медленнее, чем
возрастает медленнее, чем  ,
,
т. е.  . Результирующая сила будет направлена вправо. Под ее действием заряд q3 возвращается к положению равновесия. При смещении q3 вправо сила
. Результирующая сила будет направлена вправо. Под ее действием заряд q3 возвращается к положению равновесия. При смещении q3 вправо сила  убывает быстрее, чем
убывает быстрее, чем  , т.е.
, т.е.  , результирующая сила направлена влево и заряд q3 опять будет возвращаться в положение равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда q3 несущественна.
, результирующая сила направлена влево и заряд q3 опять будет возвращаться в положение равновесия. При отрицательном заряде равновесие является устойчивым. Величина самого заряда q3 несущественна.
Пример 2. В вакууме образовалось скопление зарядов в виде тонкого длинного цилиндра с объемной плотностью r =1·10-10 Кл/м3 и радиусом R = 10 см. Найти напряженность поля в точках, отстоящих от оси цилиндра на расстоянии 5 см и 15 см, а также вид зависимости Е (r).
| Дано: R = 10 см r=1·10-10 Кл/м3 r1 = 0,05 м r2 = 0,15 м ε = 1 Е1 =? Е2 =? Е(r) =? | Решение: Через точки 1 и 2 проведем в виде цилиндров радиусом r 1 и r 2 замкнутые поверхности (рис.2). Поток вектора напряженности, пронизывающий боковую поверхность цилиндра радиуса r 1, равен: NE(1) = E 1×2 pr 1 × l, (1) где l - длина образующей цилиндра. Поток через основания цилиндра равен нулю. По теореме Гаусса: | |||||||||||
|
 . .
Учитывая уравнение (1) получим:
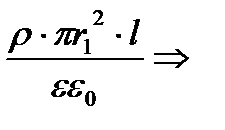 
Точка 1 находится внутри цилиндра радиуса R. Поэтому для любой точки с
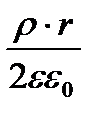 , ,
| |||||||||||
т.е. напряженность линейно растет с увеличением расстояния.
Поток напряженности, пронизывающий поверхность второго

| (5) |
По теореме Гаусса NE(2) =  =
= 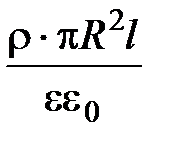 . (6)
. (6)
Приравнивая правые части выражений (5) и (6), найдем:
E2 =  . (7)
. (7)
Зависимость Е (r) при r > R имеет вид:
| (8)) |

Видно, что напряженность убывает пропорционально 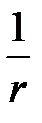 . При r = R
. При r = R
| (9) |
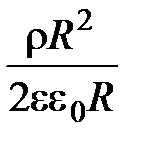 =
= 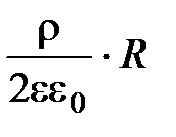
Из выражения (9) видно, что на поверхности цилиндра напряженность имеет максимальную величину.
Проверим единицы напряженности
[ E ] = 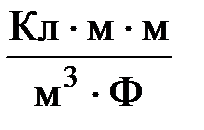 =
=  =
=  .
.
Произведем вычисления учитывая, что 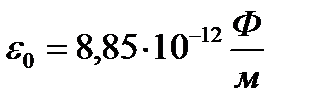

E2 = 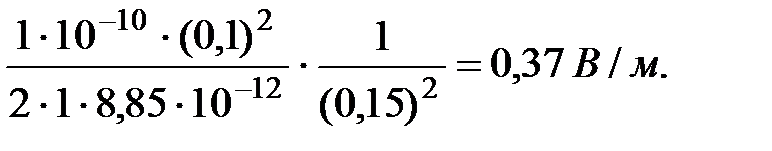
Графически зависимость Е (r) представлена на рис.3.
Таблица 2
| r | 0 | R | 2R | 3R | 4R | 5R | R 6 | 7R |
| Е | 0 | ER | ER/2 | ER/3 | ER/4 | ER/5 | ER/6 | ER/7 |
E
ЕR
Рис.3
0 R 2R 3R 4R 5R 6R 7R r
0 R 2R 3R 4R 5R 6R 7R r
Пример 3. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью υ1 =106 м/с, чтобы скорость его возросла в 2 раза.
| Дано: υ1 =106 м/с υ2 / υ1= 2 | Решение: Ускоряющую разность потенциалов можно найти, вычислив работу А сил электростатического поля. Эта работа определяется произведением элементарного заряда е на разность потенциалов U: |
| U-? |
A=eU. (1)
Работа сил электростатического поля в данном случае равна изменению кинетической энергии электрона:
 (2)
(2)
где Т1 и T2 — кинетическая энергия электрона до и после прохождения ускоряющего поля; m — масса электрона;  -
-
начальная и конечная скорости электрона.
Приравняв правые части равенства (1) и (2), и учитывая, что υ2 =2 υ1 получим:
| (3) |

Отсюда искомая разность потенциалов равна:
| (4) |

Произведем вычисления, учитывая, что масса электрона
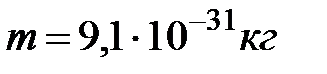 , а заряд
, а заряд 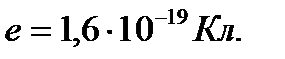

Пример 4. Как изменится емкость плоского воздушного конденсатора, если между его обкладками поместить стеклянную пластину (e = 6), толщина которой равна половине расстояния между обкладками?
Решение:
| А D В Рис. 4 |
Емкость плоского конденсатора AB до введения стеклянной пластины равна:
c0 = 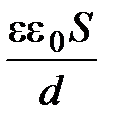 , (1)
, (1)
где S - площадь одной пластины, d - расстояние между обкладками
e - диэлектрическая проницаемость среды, e0 - дэлектрическая постоянная.
Тогда с учетом формулы (1) емкости конденсаторов сAD =2 c0, а cDB = 2e·с0
Емкость конденсатора AB после введения стеклянной пластины будет равна c'. Эту емкость можно найти по формуле:
 =
=  или
или  =
= 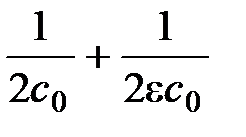 =
= 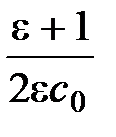 . (2)
. (2)
Выразив c' из (2), получим:
c' = 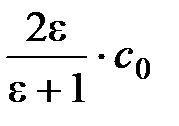 =
= 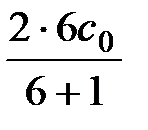 = 1,7c0. (3)
= 1,7c0. (3)
Из выражения (3) видно, что емкость конденсатора AB увеличилась в 1,7 раза.
Задачи для самостоятельного решения
001. Шарик массой m = 1г, несущий заряд q = 98 нКл, подвешен в воздухе на тонкой шелковой нити. При приближении к нему заряда противоположного знака на расстояние l = 4 см нить отклонилась от вертикального направления на угол 450. Определить величину этого заряда.
q = 18 нКл
002. На одинаковых капельках воды находится по одному лишнему электрону. Каков радиус капелек, если сила электростатического отталкивания уравновешивает силу гравитационного притяжения?
R = 16,5 мкм
003. На нити подвешен заряженный шар массой m = 300 г. Когда к нему поднесли снизу на расстояние l = 40 см заряженный таким же зарядом шар радиусом R = 2 см, то сила натяжения нити умень-шилась в четыре раза. Найти поверхностную плотность заряда на поднесенном шаре.
σ = 125 мкКл/м2
004. Сплошная металлическая сфера радиусом R = 20 см несет равномерно распределенный заряд с поверхностной плотностью σ = 1 нКл/м2. Определить напряженность электрического поля в точке, находящейся на расстоянии l = 36 см от центра сферы.
Е = 34,5 В/м
005. Сплошная металлическая сфера радиусом R = 20 см несет равномерно распределенный заряд с поверхностной плотностью
σ = 1 нКл/м2. Определить потенциал электрического поля в центре сферы и в точке, находящейся на расстоянии l = 36 см от ее центра.
φ1 = 0; φ2 = 12,42 В
006. Электрон, пролетая в электрическом поле путь от точки А к точке В, увеличил свою скорость от υ1 = 1∙106 м/с до υ2 = 3∙106 м/с. Найти разность потенциалов между точками А и В.
φ1 - φ2 = 22,75 В
007. Какая работа совершается при перемещении точечного заряда q = 0,2 нКл из бесконечности в точку, находящуюся на расстоянии
l = 1 см от поверхности сферы радиусом R = 1 см с поверхностной плотностью заряда σ = 1 нКл/см2 ?
А = - 113мкДж
008. Определить электроемкость конденсатора, для изготовления которого использовали ленту алюминиевой фольги длиной l = 157 см и шириной b = 90 мм. Толщина парафинированной бумаги d = 0,1 мм, а ее диэлектрическая проницаемость ε = 2.
С = 25 нФ
009. Как изменится емкость плоского воздушного конденсатора, если между его обкладками поместить стеклянную пластину, диэлектрическая проницаемость которой ε = 6, длина которой равна половине длины пластин конденсатора?
Увеличится в 3,5 раза
010. Два одинаковых конденсатора переменной емкости соединены в блок. В каких пределах можно изменять емкость этого блока? Емкость каждого конденсатора изменяется от 15 до 250 пФ.
От 7,5 пФ до 500 пФ
ЭЛЕКТРОДИНАМИКА
· Сила тока:
I = q/t,
где q - заряд, прошедший через поперечное сечение проводника за время t.
· Плотность тока:
j = I/S,
где S - площадь поперечного сечения проводника
· Закон Ома:
а) для участка цепи, не содержащего ЭДС:

где j1 - j2 = U - разность потенциалов (напряжений) на концах участка цепи, R - сопротивление участка;
б) для замкнутой (полной) цепи:
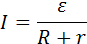
где R - внешнее сопротивление цепи, r - внутреннее сопротивление цепи, 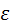 – эдс источника.
– эдс источника.
· Сопротивление проводника:

где r - удельное сопротивление проводника,  - длина проводника, S - площадь поперечного сечения проводника.
- длина проводника, S - площадь поперечного сечения проводника.
· Сопротивление системы проводников:
а) при последовательном соединении:

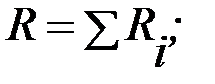
б) при параллельном соединении:

где Ri - сопротивление i -того проводника.
· Работа электрического тока:

Первая формула справедлива для любого участка цепи, на концах которого поддерживается напряжение U, последние две – для участка, не содержащего эдс, t – время.
· Закон Джоуля-Ленца:
 Q = I2Rt.
Q = I2Rt.
Примеры решения задач
Пример 5. Сила тока в проводнике сопротивлением R = 20Ом нарастает в течение времени Dt = 2 с по линейному закону от I0= 0до I = 6 А (см.рис.5). Определить теплоту Q, выделившуюся в этом проводнике за вторую секунду.
| Дано: Dt = 2 с I0 = 0 A I = 6 А Q -? | Решение:
I, A
|
Закон Джоуля-Ленца в виде Q = I2Rt справедлив для случая постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде:
dQ = I2Rdt. (1)
Здесь сила тока I является некоторой функцией времени. В нашем случае сила тока равна:
I = k t, (2)
где k - коэффициент пропорциональности, численно равный приращению силы тока в единицу времени:
 . (3)
. (3)
С учетом (2) формула (1) примет вид
 . (4)
. (4)
Для определения теплоты, выделившейся за конечный промежуток времени Dt, выражение (4) надо проинтегрировать в пределах от t1 до t2:
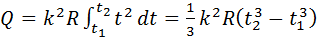 (5)
(5)
При определении теплоты, выделившейся за вторую секунду, пределы интегрирования t1= 1с, t2 = 2 c и, следовательно, Q равно:
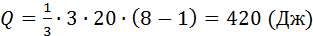 .
.
Пример 6. В цепь, состоящую из аккумулятора и сопротивления R= 10 Ом, включают вольтметр, сначала последовательно, затем параллельно сопротивлению R. Оба показания вольтметра одинаковы. Сопротивление вольтметра Rv= 1000 Ом. Каково внутреннее сопротивление аккумулятора?
| Дано: R = 10 Ом Rv = 1000 Ом U1 = U2 r =? | Решение: Показания вольтметра одинаковы, зна-чит, падение напряжения на вольтметре в первом случае (последовательное соединение), равно падению напряжения на вольтметре и при параллельно включенном сопротивлении во втором случае. |
Подсчитаем силу тока и падение напряжения на вольтметре в обоих случаях. Пусть e - эдс аккумулятора, r - его внутреннее сопротивление.
1.Ток в цепи при последовательном включении вольтметра (рис.6 а) равен:

Падение напряжения на вольтметре равно:

2. Ток в цепи при параллельном включении вольтметра (рис.6 б) равен:

| Рис. 6 |
| R |
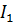
|
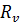
|
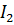
|
| R |
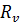
|
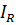
|
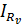
|
| а |
| б |
| r |
| r |
Общий ток  в цепи при параллельном включении вольтметра будет равен сумме токов, проходящих через сопротивления R и Rv:
в цепи при параллельном включении вольтметра будет равен сумме токов, проходящих через сопротивления R и Rv:
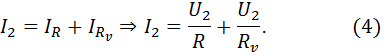
Подставляя уравнение (4) в (3) получим:
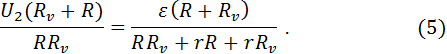
После преобразований найдем выражение для 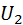 :
:

Условие U1=U2 означает, что уравнение (2) равно уравнению (6).
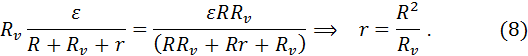
Подставляя численные значения физических величин в формулу (8) найдем внутреннее сопротивление аккумулятора:
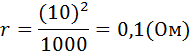
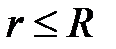 имеем:
имеем: