011.Определить заряд, прошедший по проводу с сопротивлением 30 Ом при равномерном нарастании напряжения на концах провода от 2 В до 4 В в течение 20 с.
q = 20 Кл
012. Сила тока в проводнике меняется со временем по закону I = 4+2 t. Какой заряд проходит через поперечное сечение проводника за время от 2 с до 6 с? При каком постоянном токе через поперечное сечение проводника за тоже время проходит тот же заряд?
q = 48 Кл, I = 12 А
013.Сила тока в проводнике сопротивлением 20 Ом нарастает по линейному закону от 0 до 6 А в течение 2 с. Определить теплоту, выделившуюся в этом проводнике за первую и за второю секунды.
Q1 =60 Дж, Q2 =420 Дж
014. Определить плотность тока в железном проводнике длиной 10 м, если провод находится под напряжением 6 В.
j = 6,1 МА/м2
015. Ламповый реостат состоит из пяти электрических лампочек сопротивлением 350 Ом каждая, включенных параллельно. Найти сопротивление реостата, когда горят все лампочки и когда вывинчиваются три лампочки.
R1 = 70 Ом, R2 =175 Ом
016. Батарея для карманного фонаря с эдс 4,5 В при включенной лампочке дает напряжение 4 В. Во сколько раз сопротивление лампочки больше внутреннего сопротивления батареи?
В 8 раз
017. Источник тока с эдс 36 В имеет внутренне сопротивление 6 Ом. Какое значение будет иметь сила тока в цепи при подключении к этому источнику резистора сопротивлением 12 Ом?
I = 2 А
018. Эдс батареи 9 В. При замыкании ее на внешнее сопротивление 2 Ом она дает ток силой 3 А. Определить силу тока короткого замыкания.
I = 9 А
019. Определить КПД мотора мощностью 6 кВт, если сила потребляемого тока 80 А при напряжении 110 В.
η = 68%
020. Скоростной лифт с КПД 92% включается в сеть напряжением 220 В. Чему равна сила тока в моторе, если лифт весит 15,7 кН и поднимается со скоростью 1 м/с?
I = 78 А
ЭЛЕКТРОМАГНЕТИЗМ
· Связь магнитной индукции 
с напряженностью 
магнитного поля:
где m - магнитная проницаемость изотропной среды;
m0 - магнитная постоянная (m0 = 4 p .10-7 Гн/м).
В вакууме m = I, и тогда магнитная индукция в вакууме равна:
.
· Магнитная индукция в центре кругового тока:
где R – радиус кругового витка.
· Магнитная индукция поля бесконечно длинного проводника с током равна:
где r0 - расстояние от оси проводника до точки, в которой вычисляется магнитная индукция.
· Магнитная индукция поля, создаваемого отрезком провода с током (см. рис.7, а):
Обозначения ясны из рисунка. Направление вектора магнитной индукции 
обозначено точкой - это значит, что направлен перпендикулярно плоскости чертежа к нам.
При симметричном расположении концов провода относительно точки, в которой определяется магнитная индукция (см. рис7, б) магнитная индукция равна:
|
| I |
| I |
|
|
|
|
| α |
| α |
|
|
|
| а |
| б |
| Рис.7 |
· Магнитная индукция поля соленоида:
В = mm0nI,
где n - число витков соленоида, приходящееся на единицу длины.
· Сила Ампера. Сила, действующая на прямой отрезок проводника в однородном магнитном поле равна:
,
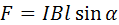где l – длина проводника, 
- угол между направлением тока в проводнике и вектором магнитной индукции , 
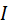- сила тока в проводнике.
· Сила Лоренца. Сила, действующая на заряженную частицу, движущуюся в магнитном поле равна:
,
- скорость заряженной частицы, - угол между векторами 
· Магнитный поток в однородном магнитном поле равен:
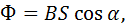
где 
- площадь плоского контура,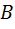 
- индукция магнитного поля, 
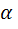- угол между нормалью к плоскости контура и вектором магнитной индукции.
· Потокосцепление (полный поток):
Эта формула верна для соленоидов и тороида с равномерной намоткой плотно прилегающих друг к другу 
витков.
· Работа по перемещению замкнутого контура в магнитном по- ле равна:
где 
- ток, протекающий в контуре,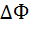 
- изменение магнитного потока, пронизывающего поверхность, ограниченную контуром.
· Закон Фарадея. Электродвижущая сила 
индукции, возникающая в замкнутом контуре, пропорциональна скорости 
изменения магнитного потока со временем:
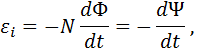
где знак минус обусловлен правилом Ленца: индукционный ток направлен так, чтобы своим магнитным полем препятствовать изменению основного магнитного поля, – число витков контура, 
– потокосцепление.
· Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур:
где R - сопротивление контура.
· Электродвижущая сила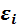 
самоиндукции, возникающая в замкнутом контуре при изменении силы тока в нем, пропорциональна скорости изменения силы тока 
:
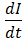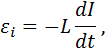
где L 
– индуктивность (коэффициент самоиндукции) контура.
· Индуктивность соленоида:
L = mm0n2V,
где n - число витков, приходящихся на единицу длины соленоида,
V - объем соленоида.
· Энергия W магнитного поля, создаваемая соленоидом с индуктивностью L, определяется формулой:
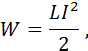
где 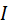- сила тока в соленоиде.
Примеры решения задач
Пример 7. По проводу, согнутому в виде квадрата со стороной а = 10 см течет ток силой I = 100 A. Найти магнитную индукцию 
в точке А пересечения диагоналей квадрата.
| Дано: а = 0,1 м I = 100 A | Решение:
Расположим квадратный виток в плоскости чертежа (см. рис.8). Согласно принципу суперпозиции магнитных полей, магнитная индукция поля квадратного витка будет равна
|
| -?
|
геометрической сумме магнитных индукций полей, создаваемых каждой стороной квадрата в отдельности:
| • |
| I |
| a |
|
|
|
|
| A |
| Рис.8 |
|
|
|
|
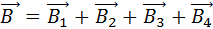(1)
В точке A пересечения диагоналей все векторы индукции будут направлены перпендикулярны плоскости витка «к нам». Кроме того, из соображения симметрии следует, что абсолютные значения этих векторов одинаковы: В1=В2=В3=В4. Это позволяет векторное равенство (1) заменить скалярным равенством:
В = 4В1. (2)
Магнитная индукция В1 поля, создаваемого отрезком прямолинейного провода с током, выражается формулой:
Учитывая, что a2 = p - a1 и cosa2 = -cosa1, формулу (3) можно переписать в виде:
.
Подставив это выражение В1 в формулу (2), найдем:
Заметив, что r0 = a/2 и cos a1 = 
(так как a1 = p/4), получим:
Подставив в эту формулу числовые значения физических величин, произведем вычисления:
Пример 8. Электрон, пройдя ускоряющую разность потенциалов U= 400 В,попал в однородное магнитное поле напряженностью Н= 103А/м. Определить радиус R кривизны траектории. Вектор скорости перпендикулярен линиям поля.
Дано:
U = 400 В
H = 103 A/м
 
mе = 9,11.10-31 кг
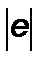 = 1,60.10-19 Кл
m0 = 4p∙.10-7 Гн/м
R =?
| Решение:
Радиус кривизны траектории электрона определим исходя из следующих сообра - жений: на движущийся в магнитном поле электрон действует сила Лоренца (дейст -
вием силы тяжести можно пренебречь):
где е - заряд электрона, u скорость электрона, В - магнитная индукция, a - угол между направлением вектора скорости  и вектором 
|
Сила Лоренца перпендикулярна вектору скорости и, следовательно, играет роль центростремительной силы:
где m - масса электрона, u скорость электрона, R - радиус кривизны траектории.
Эти силы равны. Учитывая, что по условию задачи ^ , угол a = 90 0, а sin a = 1 найдем радиус кривизны траектории:
Для нахождения скорости электрона воспользуемся законом сохранения энергии 
Работа, совершаемая электрическим полем, равна:
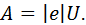(4)
Эта работа идет на увеличение кинетической энергии электрона:
Приравнивая правые части уравнений (4) и (5), найдем скорость электрона прошедшего ускоряющую разность потенциалов U = 400 В:
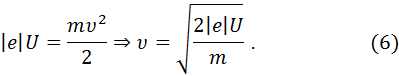
Подставив найденные выражения u в формулу 
и учитывая, что В = m0Н, определим:
Подставим численные значения величин в формулу 
и произведем вычисления:
Пример 9. Соленоид с сердечником из немагнитного материала содержит N = 1200 витков провода, плотно прилегающих друг к другу. При силе тока I = 4 А магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида.
| Дано: N = 1200 I = 4 А Ф = 6×10-6 Вб | Решение:
Индуктивность L связана с потокосцеплением  и силой тока I соотношением:
 (1)
Потокосцепление, в свою очередь, может быть выражен через поток Ф и число витков N:
|
| L=? W=? |
(2)
Из выражения (1) и (2) находим интересующую нас индуктивность соленоида:
Подставим численные значения величин в формулу и произведем вычисления:
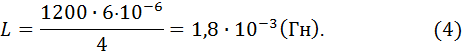
Энергия магнитного поля соленоида может быть вычислена по формуле:
где L – индуктивность соленоида, I – сила тока, протекающего по его обмотке.
Подставив в эту формулу полученное ранее выражение индуктивности (4) и, произведя вычисления, получим:
