Задача 5.Динамика точки.

 

Материальной точке сообщается начальная скорость v ₀ = 7 м/с, в результате чего она проходит по горизон­тальной шероховатой плоскости расстояние l = 10,1 м и падает с нее. Коэффициент трения скольжения f = 0,2. Определить скорость v, длину полета L, глубину падения Н точки в мо­мент t = 5 с после начала движения. Сопротивление среды не учитывать (рис. 51).

 

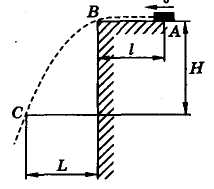
Рис. 51 Рис. 52

 

Решение. Рассмотрим движение точки на прямолинейном участке АВ (рис. 52). Определим скорость точки в кон­це этого участка. Начало осей коор­динат совместимо с началом движе­ния. Начальные условия при t = 0 имеют вид

 

 

На основании принципа освобождаемости от связей рассматриваем точку как свободную, на которую действует сила тяжести mg, нормальная ре­акция N и сила трения F_mp.

Дифференциальные уравнения движения материаль­ной точки в декартовых осях:

,

 

в данном случае с учетом того, что и , принимают вид

 

 

Отсюда N = mg. Используя закон Кулона для силы трения F_mp = fN, получаем F_mp = fmg. Тогда

. (*)

 

Разделим переменные t и v_x в уравнении (•) и проин­тегрируем его, пользуясь неопределенными интегралами

 

.

 

Учитывая начальное условие, определим постоянную интегрирования С ₁ = v ₀. Тогда формула изменения скоро­сти точки на участке АВ принимает вид

 

. (**)

 

Если же пользоваться определенными интегралами, то необходимость в постоянной интегрирования отпадает. Из (*) получаем

 

.

 

Здесь нижние пределы интегралов соответствуют на­чальным условиям, а верхние — произвольному моменту времени.

Из последнего уравнения находим , дела­ем подстановку и получаем то же решение: .

Для того чтобы вычислить время t ₁ преодоления ма­териальной точкой пути АВ и ее скорость в момент про­хождения точки В, необходимо использовать условие | АВ | = l = 10,1 м.

При этом возможны два варианта дальнейшего реше­ния задачи.

1. Перепишем уравнение (**), учитывая, что v_x =dx/dt,

 

.

 

Разделив здесь переменные и проинтегрировав (напри­мер, с использованием определенных интегралов) это уравнение, получим

 

,

откуда

.

 

Из последнего уравнения можно определить время, когда величина х будет равна l. Решая квадратное уравне­ние или , отыски­ваем два значения: t с и t₁ = 5,1 с. Второе значение времени физически не реализуется, так как предполагает дальнейшее движение точки по горизонтали, а затем воз­врат ее в точку B, что невозможно, поскольку после точки В материальная точка перестает взаимодействовать с по­верхностью и начинает падать.

Таким образом, время t ₁= 2 с и, подставляя его в фор­мулу (**), находим скорость точки в конце участка АВ: м/с.

 

Рассмотрим далее криволи­нейное движение точки на участ­ке ВС (рис. 53). Начало отсчета времени совме­стим с моментом начала падения. Начальные условия в выбранных осях координат принимают вид:

при t = 0

х = 0; = 3,1 м/с; у = 0; = 0.

 

Рис. 53

 

На точку действует только сила тяжести mg. Запи­шем дифференциальные уравнения движения точки:

,

или

.

 

Разделив переменные и проинтегрировав эти уравне­ния, получим

 

v_x = C ₃; v_y = gt + C ₄.

 

В соответствии с начальными условиями постоянные интегрирования равны С ₃ = v ₁ и С ₄ = 0.

Тогда имеем v_x = v ₁ = const, v_y = gt.

Рассматриваемое время свободного падения точки, от­считываемое от положения В, равно t ₂ = t – t ₁ = 3 с.

Вычислим скорость v ₂ точки в момент t ₂ = 3 с (поло­жение С на траектории)

v _{2 x} = v ₁= 3,1 м/с; v _{2 y} = gt ₂ = 29,4 м/с;

м/с.

Дифференциальные уравнения движения точки на уча­стке ВС представим в следующем виде:

.

 

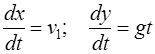Разделяя переменные и интегрируя эти уравнения, получаем

.

 

Постоянные интегрирования определяем по заданным начальным условиям (при t = 0 х = 0; у = 0), а именно: С ₅ = С ₆ = 0.

Уравнения движения точки имеют вид х = v ₁ t, у = gt ²/2.

При заданном t ₂ = 3 с находим дальность полета L = x (t ₂) = 9,3 м и глубину падения Н = y (t ₂) = 44,1 м.

Ответ: v = 29,6 м/с; L = 9,3 м; Н = 44,1 м.

№ вар.	v 0	l	f	t
			0,2.
		8,1	0,2.
		8,2	0,2.
		8,3	0,2.
		8,4	0,2.
		8,5	0,2.
		8,6	0,2.
		8,7	0,2.
		8,8	0,2.
		8,9	0,2.
			0,2.
		9,1	0,2.
		9,2	0,2.
		9,3	0,2.
		9,4	0,2.
		9,5	0,2.
		9,6	0,2.
		9,7	0,2.
		9,8	0,2.
		9,9	0,2.

Вопросы для защиты задачи

 

1. Сформулируйте законы динамики.

2. Запишите дифференциальные уравнения движения матери­альной точки в проекциях на оси прямоугольной декартовой системы координат.

3. Запишите дифференциальные уравнения движения материальной точки в проекциях на естественные оси.

4. Сущность первой задачи динамики и порядок ее решения.

5. Сущность второй задачи динамики и порядок ее решения.