Глава 3. Расчёт адаптивной системы регулирования скорости электропривода

Адаптивные системы управления целесообразно применять для приводов (электромеханических объектов управления – ЭМО), характеризующихся неопределенностью или нестационарностью параметров.

В данной работе в качестве ЭМО рассматривается двухконтурная структура подчиненного регулирования, в которой пренебрегают явлением упругости механической связи двигателя и исполнительного механизма. Тогда факт изменения момента инерции механизма J_M учитывается как изменение суммарного момента инерции J=J_Д+J_M, где J_Д - момент инерции двигателя. Вариация J_M имеет место, в частности, в станочных системах.

Возможность работы с изделиями, отличающимися по своей массе, приводит к необходимости учета нестационарности момента инерции механизма J_M, который определяет величину электромеханической постоянной времени Т_ЭМ (см. формулу (1.12)).

Адаптивная система, рассчитываемая и исследуемая в данном разделе, основана на алгоритме адаптации сигнального типа с эталонной моделью (ЭМ) [8].

Варианты заданий к курсовой работе даны в табл. 3.1 и определяются преподавателем; параметры системы ЭП приведены в табл. 3.2.

 

Техническое задание на курсовую работу

Выполнить расчеты параметров адаптивной системы ЭП, построенной по принципу подчиненного регулирования, исследовать на ЭВМ переходные процессы в синтезированной системе при управляющих и возмущающих воздействиях в условиях нестационарности параметров объекта.

Базовая структура – двухконтурная структура подчиненного регулирования, изображенная на рис.2,а.

Момент инерции механизма считается постоянным в процессе одной реализации, но его величина может быть любой из заданного допустимого диапазона значений.

Диапазон изменения приведенного к валу двигателя момента инерции механизма J_M:

J_Mmin=_________ J_Д; J_Mmax=____________ J_Д.

Момент сопротивления производственного механизма изменяется в динамике скачком на величину М_с=0,5М_н, где М_н – номинальный момент двигателя.

Параметры системы подчиненного регулирования представлены в табл. 3.2.

Требования к САУ:

- статическая ошибка замкнутой системы n_зс, £_________,%;

- перерегулирование при единичном входном сигнале s, £________,%;

- время переходного процесса t_пп£_______с.

В начале пояснительной записки следует указать выбранный вариант технического задания, а затем представить необходимые расчеты, руководствуясь методическими указаниями, приведенными ниже к отдельным этапам проектирования САУ.

 

Таблица 3.1

Варианты заданий к курсовой работе

 

№ варианта	JД, кгм2	JМ Н, кгм2	JMmin, кгм2	JMmax, кгм2	tпп, c	s, %	ест, %
	3,8	10 JДВ	5JДВ	20JДВ	0,5
	3,8	5 JДВ	JДВ	15JДВ	0,5		0,5
	10,3	10 JДВ	5JДВ	20JДВ	0,5
	6,0	10 JДВ	5JДВ	20JДВ	0,5
	7,0	10 JДВ	5JДВ	20JДВ	0,5
	7,0	10 JДВ	3JДВ	20JДВ	0,5
	5,9	5 JДВ	5JДВ	15JДВ	0,5		0,5
	7,0	5 JДВ	JДВ	15JДВ	0,5		0,5
	6,0	20 JДВ	JДВ	30JДВ	0,5
	7,0	5 JДВ	JДВ	20JДВ	0,5		0,5

 

Таблица 3.2

Параметры системы электропривода

 

№ варианта	РС	РТ	kП	ТП, с	RЯЦ, ОМ	ТЯ, с	kД, 1/Вс	ТЭМ, с	kОТ, В/А	kОС, Вс	ТДТ, с	ТДС, с	kФ, Вс
β1	τ1, с	β2	τ2, с
		0,09	0,34	0,033		0,004	0,07	0,033	0,36	0,4	0,01	0,06	0,002	0,01	2,74
		0,09	0,30	0,03		0,004	0,145	0,032	0,36	0,85	0,023	0,06	0,002	0,01	2,72
		0,10	0,26	0,036		0,005	0,115	0,036	0,36	0,45	0,023	0,06	0,003	0,01	2,72
	58,4	0,17	0,26	0,055		0,006	0,045	0,055	0,37	0,67	0,078	0,08	0,005	0,02	2,75
	24,7	0,13	0,03	0,04		0,005	0,045	0,04	0,28	0,21	0,013	0,06	0,002	0,02	3,49
	50,5	0,17	0,20	0,036		0,006	0,07	0,036	0,36	0,69	0,01	0,06	0,005	0,02	2,75
	50,8	0,17	0,28	0,05		0,006	0,07	0,05	0,36	0,69	0,01	0,06	0,005	0,02	2,75
	33,6	0,17	0,22	0,044		0,006	0,08	0,044	0,36	0,41	0,014	0,06	0,005	0,02	2,72
		0,15	0,02	0,031		0,005	0,07	0,032	0,36	0,26	0,01	0,06	0,004	0,02	2,74
		0,09	0,32	0,04		0,004	0,07	0,04	0,28	0,75	0,013	0,08	0,002	0,02	3,48

3.1. Решение задачи адаптивного управления с эталонными и настраиваемыми моделями

При решении задач адаптивного управления динамическими объектами применяется несколько различных подходов [8,9]. Наиболее полные результаты получены для задачи управления с эталонной моделью.

Постановка этой задачи может быть сформулирована следующим образом.

Пусть уравнения движения нелинейного объекта управления в пространстве состояний имеют вид:

(3.1)

а уравнения движения вспомогательной системы, называемой эталонной моделью (ЭМ):

(3.2)

 

где x=x(t), x_M(t) - m- мерные функция состояния системы и модели; u=u(t), r(t) - m- мерные функции управляющих воздействий; y(t), y_M(t) - l- мерные функции выходов объекта и модели, x - вектор ограниченной размерности меняющихся параметров объекта; f=f(t) - n- мерная функция внешних возмущений; x₀ - начальное состояние. Особенностью описания объекта вида (3.1) является введение вектора параметров x для обозначения нестабильности его свойств. Относительно x известна допустимая ограниченная область его значений, т. е. ограниченное множество ,
xÎ . Например, для ЭМО, в котором изменяется лишь один параметр x=J_M, множество представляет собой отрезок =[ J_Mmin, J_Mmax ].

Цель адаптивного управления, обычно задаваемая с помощью некоторого функционала качества, значения которого вычисляются по измеряемым параметрам, считается достигнутой, если указанный функционал либо принимает экстремальное значение, либо его величина находится в заданных пределах.

Кроме цели управления используется цель адаптации. Она также формализуется с помощью некоторого функционала и может либо совпадать с целью управления, либо отличаться от неё, являясь некоторой вспомогательной целью, служащей для решения основной задачи управления. Обобщенная структурная схема адаптивной системы управления представлена на рис. 3.1.

Рис. 3.1. Обобщенная структурная схема адаптивной системы

 

Адаптивная система управления имеет двухуровневую структуру. На верхнем уровне в блоке «Регулятор» производится расчет сигналов управления u(t), которые зависят от настраиваемых параметров c(t). Расчет настраиваемых параметров c(t) производится в блоке «Адаптер» на основании известной информации: сигналов задания r(t) и измеряемых выходных сигналов y(t).

При построении адаптивных систем с ЭМ как правило требуется определить закон адаптивного управления

(3.3)

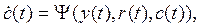(3.4)

 

не зависящий от xÎ и использующий только величины, доступные измерению, так, чтобы движение объекта приближалось с течением времени к движению ЭМ, то есть достигалась цель управления

 

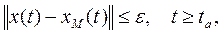(3.5)

 

для всех xÎ и всех rÎR^m, fÎ Rⁿ, где ε>0 - заданная точность, t_a - требуемое время адаптации, R - евклидово пространство соответствующей размерности.

Эталонная модель выбирается таким образом, чтобы она обладала устойчивостью и заданным качеством переходных процессов. При этом ЭМ может быть либо явно реализована в системе управления в виде отдельного динамического звена (3.2) (система с явной эталонной моделью), либо присутствовать в системе неявно, в виде набора параметров алгоритма управления (системы с неявной ЭМ). В последнем случае цель управления (3.5) обычно заменяется другой, в формулировке которой не используется вектор x_M(t), например:

(3.6)

В работе [12] показано, что при устойчивой ЭМ (3.2) из выполнения цели (3.6) при достаточно малых ε₁>0 следует выполнение цели (3.5).

При помощи вспомогательных целевых функционалов можно задавать также вспомогательные цели управления, с помощью которых зачастую бывает легче синтезировать закон адаптации

(3.7)

или

(3.8)

Обычно V(x) -квадратичный функционал; V(x)=x(t)^TPx(t),где P=P^T>0 - положительно определенная матрица.

При синтезе закона адаптивного управления (алгоритма адаптации) также часто вводят вспомогательные цели, называемые целями адаптации (ЦА). В зависимости от задания ЦА при выборе структуры адаптивного регулятора (АР) возможны различные пути.

1. В первом случае структура основного контура системы (регулятора (3.3)) выбирается так, чтобы обеспечить совпадение динамики замкнутой системы и ЭМ при некоторых значениях параметров регулятора (условие согласованности объекта и ЭМ). Это значит, что для любого xÎ должен существовать вектор '' идеальных'' значений параметров регулятора такой, что

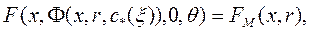(3.9)

 

(не измеряемыми возмущениями f(t) при синтезе АР в первом приближении пренебрегают, полагая f(t)≡0).

При выборе алгоритма адаптации ставится цель приближения движения замкнутой системы к эталонному, то есть ЦА задается в виде (3.5) - (3.8). Осуществляться адаптация может либо за счет измене­ния (настройки) вектора параметров с(t) основного регулятора (параметрическая адаптация), либо с помощью введения дополнительного сигнала в регулятор (сигнальная адаптация) (3.3). Значения параметров с(t) в последнем случае выбирают усредненными постоянными (c(t)= 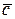), соответствующими номинальному режиму объекта управления, а структура

АР сигнального типа описывается уравнением

(3.10)

где z(t) - дополнительный сигнал адаптации.

Алгоритмы сигнальной адаптации обладают бόльшим быстродействием и менее громоздки, но работоспособны в более узком диапазоне изменения параметров объекта, чем алгоритм параметрического типа. Если для работы основного контура или контура адаптации требуется измерение всех переменных состояния объекта управления, то в систему может быть введен наблюдатель [9]. Если диапазон возможных значений параметров объекта не слишком велик, то параметры наблюдателя можно рассчитывать для номинального режима, то есть, считая динамику замкнутой системы совпадающей с эталонной. Другой метод адаптивного управления при неполном измерении вектора состояния объекта заключается во введении в систему дополнительных фильтров [9]. Описанный подход называют прямым, так как при нем цель адаптации совпадает с целью управления и состо­ит в приближении движения объекта к ЭМ.

2. При втором подходе структура и параметры основного контура также выбираются исходя из структуры объекта в предположении, что его параметры известны и таким образом, чтобы обеспечить достижение исходной или вспомогательной цели управления. Однако при работе системы вместо параметров объекта ξ (которые на самом деле неизвестны) используются их оценки , обеспечиваемые алгоритмом адаптации. Таким образом, регулятор описывается вместо уравнения (3.3) уравнением

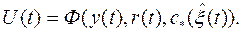(3.11)

Для осуществления адаптации вводится вспомогательная система, структура которой совпадает со структурой объекта - так называемая настраиваемая модель (НМ) объекта управления

(3.12)

Параметры настраиваемой модели и есть оценки вектора ξ, получаемые при помощи алгоритма адаптации

(3.13)

Цель адаптации, исходя из которой строится алгоритм адаптации (3.13), состоит в приближении вектора состояния 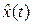HM (3.12) к состоянию объекта x(t):

(3.14)

НМ так же, как и эталонная модель, может присутствовать в системе неявно.

Тогда ЦА, аналогично (3.6), задается соотношениями

(3.15)

а в алгоритм адаптации (3.13) вектор 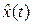не входит.

Если для реализации алгоритмов регулирования или адаптации требуется знание фазовых координат, недоступных измерению, то в систему может быть введен наблюдатель. Параметры наблюдателя удобно выбирать, исходя из имеющихся текущих оценок параметров объекта. Иногда оценивание параметров объекта осуществляется совместно с оцениванием состояния, то есть наблюдатель оказывается адаптивным.

При описанном подходе ЦА не совпадает с целью управления и состоит в приближении движения настраиваемой модели к движению объекта (идентификации). Поэтому этот подход называют непрямым или идентификационным. Идентификационный подход позволяет применять более сложные законы регулирования, чем прямой подход. В частности, в этом случае широко используется принцип модального управления. Разделение целей адаптации и управления дает возможность независимо синтезировать основной контур и контур адаптации, что облегчает построение адаптивного регулятора. С другой стороны, затрудняется обоснование работоспособности системы, так как из достижения ЦА не следует непосредственно достижение цели управления.

Для синтеза алгоритмов адаптации по заданному целевому функционалу применяются различные методы: градиентный метод с использованием функций чувствительности, метод функций Ляпунова, метод рекуррентных целевых неравенств, метод скоростного градиента и другие [9, 12].

3. Возможны промежуточные варианты построения адаптивных систем. Например, структура системы может выбираться на основа­нии прямого подхода, а для восстановления состояния объекта может использоваться адаптивный наблюдатель.

 

3.2. Построение структуры адаптивной системы управления с эталонной моделью для линейного электромеханического объекта

Как указывалось выше, электропривод можно рассматривать как линейную стационарную систему, один из параметров которой (момент инерции механизма J_M) является неопределенным, но принимающим значения из заданной области возможных значений J_M Î [ J_Mmin, J_Mmax ].

Тогда адаптивная система управления линейным электромеханическим объектом (ЭМО) с эталонной моделью может быть описана в пространстве состояний следующим образом:

· линейная стационарная модель объекта с неизвестными заранее массо-инерционными параметрами x

(3.16)

· линейная стационарная эталонная модель, задающая желаемую динамику объекта

(3.17)

где x, x_MÎRⁿ– векторы состояния ЭМО и ЭМ соответственно; u, rÎR^m - управляющий сигнал ЭМО и задающий сигнал ЭМ, A(x), A_M - nxn - матрицы, B(x), B_M – nxm - матрицы полного ранга, rangB=m, rangB_M=m, A_M – гурвицева матрица.

Цель управления – совпадение динамики ЭМО с динамикой ЭМ, то есть

e(t)=x(t)-x_M(t)®0 (3.18)

при t®¥, где e(t) – вектор ошибки, eÎRⁿ.

Структуры ЭМО и ЭМ должны быть согласованы, что можно установить с помощью проверки условий Эрцбергера [8], устанавливающих существование mxn -матрицы K_a и mxm -матрицы K_b, являющихся решением уравнений

A-A_M=BK_a, B-B_M=BK_b. (3.19)

Физический смысл условий Эрцбергера состоит в проверке принципиальной возможности компенсации неопределенности параметров с помощью управляющих сигналов.

Алгоритм адаптации сигнального типа для такой системы имеет вид

u_a(t)= -gsign(B^TPe(t)), (3.20)

где g - коэффициент усиления, функция sign – знаковая функция:

Симметричная положительно определенная nxn -матрица P находится как решение матричного уравнения А.М. Ляпунова для матрицы A_M эталонной модели

A_M^TP+PA_M= -Q,

где Q=Q^T>0 – заданная симметричная положительно определенная nxn-матрица.

Тогда сигнал управления для ЭМО принимает вид

u(t)=r(t)-u_a(t).

 

Обобщенная схема адаптивной системы представлена на рис. 3.2.

 

Рис.3.2. Структурная схема САУ сигнального типа

3.3. Расчет параметров алгоритма адаптации

Рассмотрим типовую структуру подчиненного регулирования с контурами тока и скорости двигателя (рис. 3.3).

При настройке ПИ-регулятора тока на оптимум по модулю (ОМ) передаточная функция оптимизированного контура тока в соответствии с (1.22) имеет вид

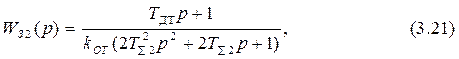
где Т_å2=Т_ДТ+Т_П.

Рис. 3.3. Структурная схема системы подчинённого регулирования скорости двигателя

 

При настройке П- или ПИ- регулятора скорости на ОМ передаточная функция замкнутого скоростного контура будет

где Т_S1=Т_ДС +2 Т_å2.

В случае настройки ПИ-регулятора скорости на симметричный оптимум передаточная функция контура скорости станет

 

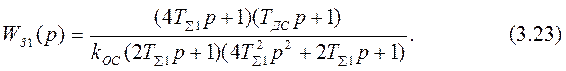
Синтез алгоритма адаптации производится по упрощенной передаточной функции оптимизированного контура скорости (Т_ДС=0) при настройке на ОМ

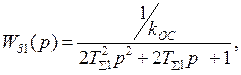(3.24)

что соответствует эквивалентному демпфированию

Выбрав в качестве переменных состояния объекта канонические координаты y(t)=x₁(t)=w(t), x₂(t)= (t), получим векторно-матричную модель контура скорости с учетом (3.24) в виде

или в матричной форме

 

Для выполнения условий структурной согласованности объекта и

эталонной модели (3.19) уравнения динамики ЭМ выбираются в виде

 

 

Характеристический полином для ЭМ в форме (3.26) рассчитывается по формуле

D_М(р)=det(pI₂-A_M)=p²-a_M2p-a_{M1 .}

В соответствии с техническим заданием на курсовую работу коэффициенты эталонной модели выбираются равными коэффициентам стандартных полиномов D_ж(р), например с распределением корней по Баттерворту (n=2):

D_ж(р)= p²+1,4w₀p+w₀².

Значение частоты w₀ определяет быстродействие системы и рассчитывается с учетом времени переходного процесса, заданного в техническом задании по формулам, представленным в разд. 2. Тогда a_M1=-w₀ ²; a_M2=-1,4w₀.

Векторно-матричная модель (3.26) соответствует ЭМ, описываемой передаточной функцией

где b₀= -(1/a_M2)=1/w₀², b₁=a_M1/a_M2=1,4/w₀ и характеризующейся, например, при w₀=35c^-1 временем переходного процесса t_ПП@0,1с и перерегулированием s =4,5%.

Структурная схема ЭМ имеет вид, представленный на рис.3.4,

где b₀=(-1/ a_M1), b₁=(- a_M2/ a_M1).

Для построения сигнального алгоритма адаптации (3.20) необходимо рассчитать элементы матрицы Р, являющейся решением матричного уравнения Ляпунова, которое при n=2 примет вид

 

 

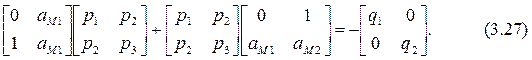
Для матрицы Р необходимо определить формулы для расчета лишь трех элементов (поскольку Р – симметричная матрица):

 

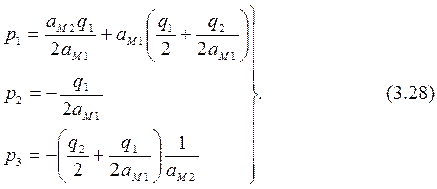
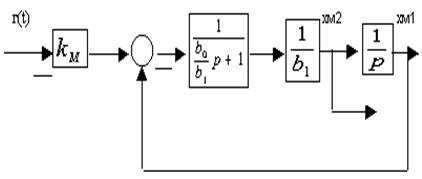
Рис. 3.4. Структурная схема ЭМ

 

Сигнал адаптации u_a(t) в соответствии с формулой (3.20) имеет вид

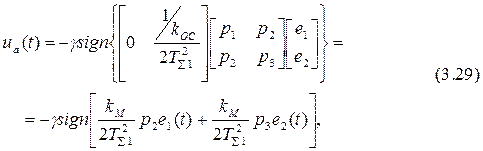
где k_M=1/k_oc.

 

Структурная схема адаптивной системы в общем виде представлена на рис. 3.5, а схема адаптивной системы с двумерным объектом (n=2) представлена на рис. 3.6; т.к. k_M>0 и 2Т_S1²>0, то формирование знака выражения, стоящего в квадратных скобках (3.29), можно проводить без учета указанных коэффициентов.

Рис. 3.5. Структурная схема адаптивной системы

 

3.4. Выбор коэффициента усиления адаптивного алгоритма

Выбор коэффициента усиления g, фигурирующего в алгоритме адаптации (3.29), регламентируется единственным требованием g>0. Наиболее эффективное значение этого параметра находится моделированием на компьютере.

Поскольку теоретический синтез алгоритма адаптации базируется на условии согласованности объекта и эталонной модели (3.19), а степень ЭМ выбрана равной двум, то и работоспособность адаптивной системы теоретически обоснована для объекта того же порядка n=2. Поэтому выбор коэффициента усиления g осуществляется по упрощенной модели структуры подчиненного регулирования, а потом качество процессов управления проверяется моделированием на компьютере для полной модели при наилучшем значении коэффициента g=g^*. Наилучшим значением коэффициента g следует считать то, при котором время переходного процесса при J_M = J_Mmin, J_M =J_Мн и J_M =J_Mmax соответствует требованиям технического задания.

Кроме того, поскольку векторно-матричная модель эталонной динамики (3.26) записана в канонических координатах , то и формирование сигналов ошибки е=[е₁, е₂]^T должно осуществляться с использованием канонических координат ЭМО .

При синтезе адаптивной СЭП выбирается П-регулятор скорости W_РС(p)=b₁, а замкнутый контур тока (ЗКТ) представляется апериодическим звеном

С учетом этого структурная схема адаптивной системы примет вид, показанный на рис. 3.6.

 

Рис. 3.6. Адаптивная система для объекта второго порядка

 

Изменение момента инерции механизма J_М отражается в изменении электромеханической постоянной времени , где J_å=J_Д+J_M. Значение Т_ЭМ, указанное в табл. 3.2, соответствует номинальному значению момента инерции механизма J_MН. Эффективность адаптивного алгоритма управления при различных значениях коэффициента g проверяется при ступенчатом входном сигнале U_зс в диапазоне изменения J_MÎ[J_Mmin, J_Mmax] с соответствующим пересчетом Т_ЭМ.

Результаты исследования оформляются в виде табл. 3.3.

 

3.5. Исследование адаптивной системы с эталонной моделью для уточненной структуры подчиненного регулирования скорости двигателя

Двухконтурная структура подчиненного регулирования скорости имеет более высокий порядок n=4, (рис. 3.7) по сравнению с упрощенной моделью (n=2), поэтому необходимо исследовать эффективность адаптивного алгоритма управления с ЭМ второго порядка и коэффициентом усиления g, выбранным в предыдущем разделе.

Таблица 3.3

№	Вариант СЭП	Значение g	Время переходного процесса tПП
при JMmin	JМн	JMmax
	СЭП без АР	g=0
	СЭП с АР	g=g1
g=g2
g=g3

Кроме того, исследование динамики адаптивной системы для данной структуры СЭП следует производить как для задающего сигнала U_зс, так и для возмущающего воздействия - момента сопротивления М_с.

Результаты исследования должны быть сведены в табл. 3.4.

 

Таблица 3.4

 

Вариант СЭП	Параметры ОУ	Значе-ние g	Время tПП, с	Перерегу- лирование s, %	Дина- мическая ошибка n, %
JM	ТЭМ
СЭП без АР	JMmin		g=0
JMн
JMmax
СЭП с АР	JMmin		g=g*
JMн
JMmax

 

3.6. Исследование динамики адаптивной СЭП с учетом ограничения выходного сигнала регулятора скорости (РС)

 

Необходимо исследовать динамику электропривода без АР и с АР с учетом ограничения выходного сигнала регулятора скорости. Соответствующий нелинейный блок БО приведён на рис. 3.7. При реализации регуляторов на элементах серии УБСР-АИ диапазон выходного напряжения РС U_РС составляет ±10 В, что и определяет параметры БО (k_БО=1). Данное исследование оформляется в виде таблицы, соответствующей по форме табл. 3.4.

 

Пояснительная записка должна содержать техническое задание, параметры исходной системы, структурные динамические схемы исходной СЭП и адаптивных систем управления, расчет параметров эталонной модели и алгоритма адаптивного управления, графики переходных процессов для адаптивной системы с упрощенной (n=2) и уточненной структурой (n=4) подчиненного регулирования скорости двигателя без учета и с учетом ограничения выходного сигнала регулятора скорости, а также показатели качества переходных процессов в неадаптивной и адаптивной системах, представленные в виде таблиц, форма которых указана в соответствующих разделах. В заключение должны быть сделаны выводы о соответствии синтезированной адаптивной системы требованиям технического задания.

____

 

Рис. 3.7. Структурная схема адаптивной СЭП с объектом 4-го порядка

 

Рекомендуемая литература

1. Родионов В.Д., Терехов В.А., Яковлев Старовато В.Б. Технические средства АСУ ТП. -М.: Высш. шк, 1989.

2. Бесекерский В.А. Попов Е.П. Теория систем автоматического регулирования. –М.: Наука, 1985.

3. Егоров В.Н., Шестаков В.М. Динамика систем электропривода. –Л.: Энергоатомиздат, 1983.

4. Репкин В.И., Шестаков В.М. Моделирование систем. Учебное пособие с грифом УМО АМ. –СПб.: СПбГПУ, 2009.

5. Теория автоматического управления. Линейные системы: Метод указ. к выполнению лабораторных работ. /В.И. Власов, О.П. Томчина.–СПб.: Изд-во ПИМаш, 1994.

6. Шестаков В.М., Дмитриев Б.Ф., Репкин В.И. Электронные устройства систем автоматического управления: Учеб. пособие. –Л.: Изд-во ПИМаш, 1991.

7. Дьяконов В. Simulink 4: Специальный справочник. СПб.:Питер,2002.

8. Борцов Ю.А., Поляхов Н.Д., Путов В.В. Электромеханические системы с адаптивным и модальным управлением. -Л.: Энергоатомиздат., 1984.

9. Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления с примерами на языке MATLAB. -СПб.: Наука, 1999.

10. Теория цифровых и нелинейных систем автоматического управления / Под ред. В.М. Шестакова. –СПб: УНЦ «Проблемы машиностроения, механики и процессов управления», 2000.

11. Алексеев А.А., Имаев Д.Х., Кузьмин Н.Н., Яковлев В.Б. Теория управления. –СПб: ГЭТУ «ЛЭТИ», 1999.

12. Фрадков А.Л. Адаптивное управление в сложных системах. М.: Наука, 1990.

 

ПРИЛОЖЕНИЕ 1

ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА

 

Санкт-Петербургский политехнический университет Петра Великого

Институт металлургии, машиностроения и транспорта

 

Кафедра «Технологические процессы и оборудование автоматизированных

машиностроительных производств»

 

 

КУРСОВАЯ РАБОТА