Уравнение (2) представляет собой дифференциальное уравнение второго порядка (вообще говоря, нелинейное), для которого нет универсального алгоритма построения решения в квадратурах. Но, как известно из курса обыкновенных дифференциальных уравнений, существуют целые классы дифференциальных уравнений, обладающих рядом специальных свойств: например, уравнение может допускать понижение порядка; может не содержать явно некоторых переменных; оказаться линейным или автономным и т.п. Эти свойства могут существенно упростить решение вариационной задачи, поэтому целесообразно находить, учитывать и классифицировать эти специальные случаи. Особенно полезна классификация, дающая возможность «предсказать» свойства уравнения Эйлера по виду функции 
.
1. 
. Уравнение Эйлера имеет вид: 
, т.е. является функциональным, а не дифференциальным.
2. 
, т.е. подынтегральная функция является линейной относительно производной. Уравнение Эйлера снова превращается в функциональное:
.
Функции, удовлетворяющие функциональным уравнениям, не образуют параметрического семейства и не обязаны удовлетворять граничным условиям.
Пример 2. Найти экстремали функционала
,
удовлетворяющие условиям: 
.
Решение. Подынтегральная функция не зависит от 
, значит, уравнение Эйлера имеет вид: 
, откуда находим единственную кривую, которая может быть экстремалью: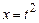 
. Но вариационная задача содержит еще граничные условия, которые для найденной кривой могут и не выполняться. В самом деле, для функции 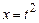имеем: 
то есть первое условие выполняется; но 
значит, если 
, то кривая 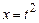является экстремалью, если же 
, то задача не имеет решения.
Пример 3. Найти экстремали функционала
,
удовлетворяющие условиям: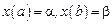 
.
Решение. Подынтегральная функция относится ко второму типу при 
, 
, а уравнение Эйлера имеет вид: 1=1, т.е. обращается в тождество. Но если равенство выполняется тождественно, то, как известно из курса интегрального исчисления, это означает, что подынтегральная функция являет собой полный дифференциал. В данном случае его легко восстановить: 
, следовательно, 
, т.е. значение функционала остается неизменным при любой дифференцируемой на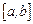 
функции. Значит, все эти функции (их бесконечное множество) являются решениями данной вариационной задачи.
3. 
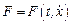. Уравнение Эйлера имеет вид: 
или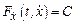 
. Таким образом, уравнение допускает понижение порядка и становится дифференциальным уравнением первого порядка.
4. 
. Решениями уравнения Эйлера могут быть только прямые: 
.
5. 
. Уравнение Эйлера снова допускает понижение порядка и принимает вид:
.
6. Как известно, из всех дифференциальных уравнений наиболее простая структура решений у линейных. Поэтому представляет интерес указать класс функционалов, для которых уравнения Эйлера – линейные. Если
,
то уравнение Эйлера имеет вид:
.
Заметим, что мы получили (в самосопряженной форме) линейное дифференциальное уравнение общего вида. Следовательно, любому линейному дифференциальному уравнению второго порядка можно сопоставить функционал (и даже не один), для которого это уравнение будет уравнением Эйлера.