С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке 
, то функция возрастает на этом промежутке;
б) если 
, то функция убывает на этом промежутке.
Пример 5. Найдите промежутки возрастания и убывания функции 
.
Решение. Найдем производную функции: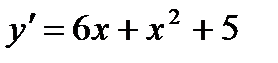 
. Чтобы найти промежутки возрастания данной функции, необходимо решить неравенство или 
, а чтобы найти промежутки убывания функции – решить неравенство или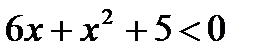 
.
Решая любое из этих неравенство методом интервалов (рис. 8.2), получим: функция возрастает на промежутке 
и на промежутке 
; функция убывает на промежутке 
.
| ||||||
| Рис. 8.2 |
Заметим, что, записывая промежутки возрастания и убывания функции, концы промежутков можно не включать ни в один из промежутков, а можно и включать в один из промежутков.
Ответ: возрастает на 
и на 
; убывает на .
Экстремум функции
Максимумом (минимумом) функции 
называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 8.3).
| |||||||
| Рис. 8.3 |
Максимум и минимум функции называются экстремумом функции. Значение аргумента, при котором достигается экстремум, называется точкой экстремума.
На рисунке 8.3 значения 
, 
, 
, 
и 
являются точками экстремума рассматриваемой функции.
Критическими точками функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение:
.
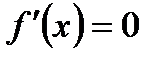Пример 7. Найдите критические точки функции
.
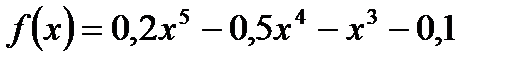Решение. Найдем производную данной функции:
.
Найдем критические точки функции, решая уравнение:
, 
, откуда:
, 
и 
.
Ответ: 
.
Алгоритм нахождения точек экстремума функции:
1) находим область определения функции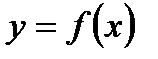 
;
2) находим 
;
3) находим критические точки функции, решая уравнение 
;
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.
Пример 8. Найдите точки экстремума функции
.
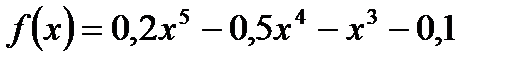Решение. Зная критические точки функции , и (см. пример 7), нанесем их на область определения данной функции и установим знаки ее производной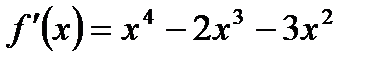 
на полученных промежутках (рис. 8.4). Согласно рисунку 8.4 запишем: 
, 
. Критическая точка 
не является точкой экстремума.
| |||||||||
| Рис. 8.4 |
Ответ: , .
Рассмотрим функцию 
на отрезке [ a; b ]. Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.
Алгоритм нахождения наибольшего и наименьшего значений функции на заданном отрезке: 1) находим ;
2) находим критические точки функции, решая уравнение ;
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Пример 9. Найдите наибольшее и наименьшее значение функции 
на отрезке 
.
Решение. 1) Найдем производную данной функции:
.
2) Найдем критические точки функции, решая уравнение
, 
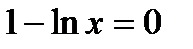, откуда 
.
3) Найдем значение функции на концах отрезка 
и в критической точке , поскольку она принадлежит данному отрезку: 
, 
, 
.
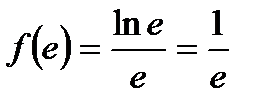4) Наибольшее значение на заданном отрезке функция принимает в критической точке и оно равно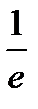 
, а наименьшее – на конце отрезка в точке 
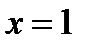и оно равно 0.
Ответ: 
; 
.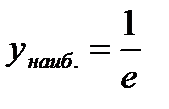