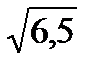Приведем схему исследования функции  .
.
1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.
Пример 11. Исследуйте функцию  и постройте ее график.
и постройте ее график.
Решение. 1. Запишем область определения функции:  .
.
2. Так как 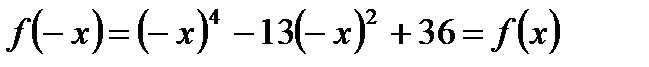 и
и 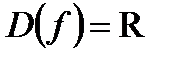 – симметричное числовое множество, то функция четная. Следовательно, график функции симметричен относительно оси Оу.
– симметричное числовое множество, то функция четная. Следовательно, график функции симметричен относительно оси Оу.
3. Функция не периодическая.
4. Так как  , то график функции пересекает ось ординат в точке
, то график функции пересекает ось ординат в точке 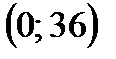 .
.
5. Найдем нули функции, решая уравнение 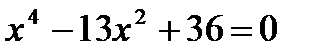 . По теореме Виета
. По теореме Виета 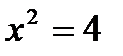 и
и 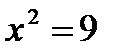 . Тогда
. Тогда  и
и 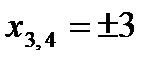 . Следовательно, график функции пересекает ось абсцисс в точках:
. Следовательно, график функции пересекает ось абсцисс в точках:
 ,
, 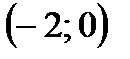 ,
, 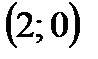 и
и  .
.
6. Исследуем функцию с помощью первой производной.
1) Найдем производную функции: 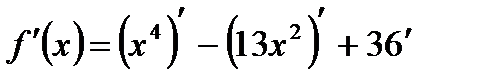 ,
, 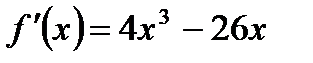 .
.
2) Найдем критические точки функции, решая уравнение: 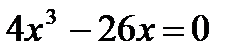 ,
,  , откуда
, откуда 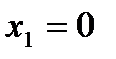 ,
, 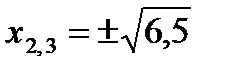 .
.
3) Нанесем критические точки на координатную прямую и определим знаки производной функции на полученных промежутках:
| ||||||||
| Рис. 8.6 |
Из рисунка 8.6 видим, что на промежутках 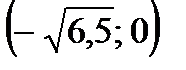 и
и  функция возрастает, а на промежутках
функция возрастает, а на промежутках  и
и  функция убывает.
функция убывает.
4) Запишем точки экстремума функции:
 ,
, 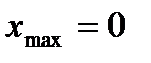 ,
, 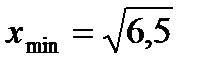 .
.
Найдем значение функции в точках экстремума:
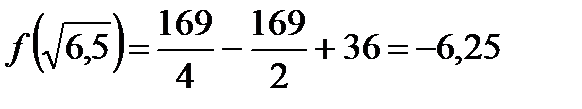 ,
, 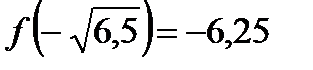 ,
, 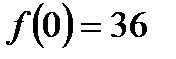 .
.
7. Исследуем функцию с помощью второй производной.
1) Найдем вторую производную функции:
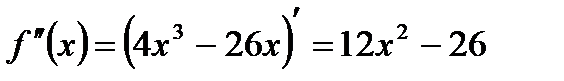 .
.
2) Найдем критические точки функции второго рода:
 ,
,  ,
, 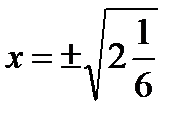 .
.
3) Нанесем критические точки на координатную прямую и определим знаки второй производной функции на полученных промежутках:
| ||||||
| Рис. 8.7 |
Точки перегиба графика функции: 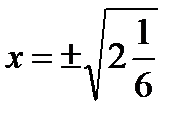 .
.
Функция выпукла вниз на промежутках
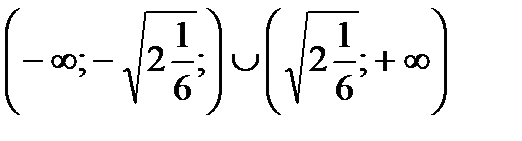 .
.
Функция выпукла вверх на промежутке 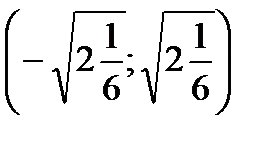 .
.
8. Найдем асимптоты графика функции.
Так как 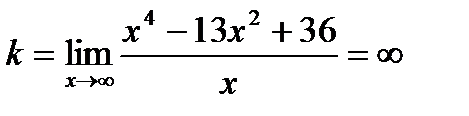 , то наклонных и горизонтальных асимптот нет. И вертикальных асимптот нет.
, то наклонных и горизонтальных асимптот нет. И вертикальных асимптот нет.
9. Построим схематически график функции (рис. 8.8):
| |||||||
| Рис. 8.8 |
10. Запишем промежутки знакопостоянства функции:
1) функция положительна (ее график расположен выше оси абсцисс) на промежутках  ;
;
2) функция отрицательна (ее график расположен ниже оси абсцисс) на промежутках  .
.
11. Запишем область значений функции:  .
.
Контрольный тест 8
Укажите правильный вариант ответа (1 – 10):
1. Функция  убывает на промежутке
убывает на промежутке
Варианты ответов: 1) 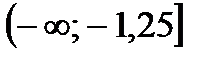 ; 2)
; 2) 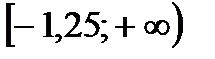 ;
;
3) 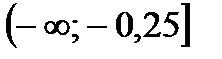 ; 4)
; 4) 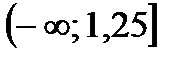 ; 5)
; 5) 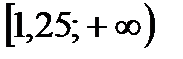 .
.
2. Наименьшее значение функция 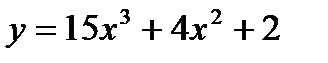 принимает в точке с абсциссой
принимает в точке с абсциссой
Варианты ответов: 1) 5; 2) 12; 3) 0; 4) 2; 5) 1.
3. Максимальное значение, принадлежащее промежутку 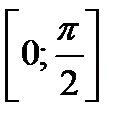 , функция
, функция 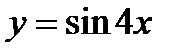 принимает в точке с абсциссой
принимает в точке с абсциссой
Варианты ответов: 1)  ; 2)
; 2) 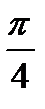 ; 3)
; 3) 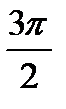 ; 4)
; 4)  ; 5)
; 5) 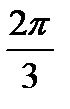 .
.
4. Нормаль, проведенная к графику функции 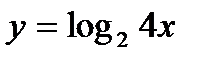 в точке
в точке 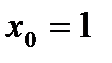 , имеет вид
, имеет вид
Варианты ответов: 1) 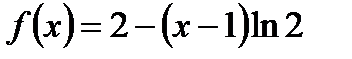 ;
;
2) 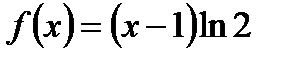 ; 3)
; 3)  ;
;
4) 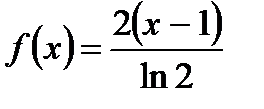 ; 5)
; 5) 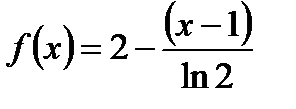 .
.
5. Касательная к графику функции  в точке
в точке 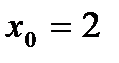 имеет вид
имеет вид
Варианты ответов: 1) 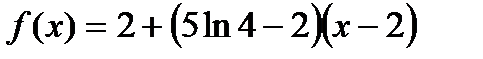 ;
;
2) 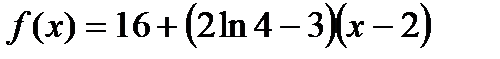 ; 3)
; 3) 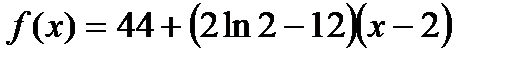 ;
;
4) 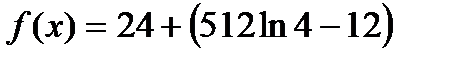 ; 5)
; 5) 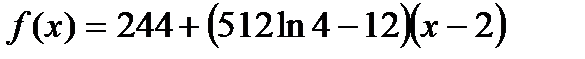 .
.
6. Наименьшее целое значение, принадлежащее промежутку, на котором функция  вогнута, равно
вогнута, равно
Варианты ответов: 1) 8; 2) 9; 3) 12; 4) – 2; 5) 10.
7. Наибольшее значение функции  на промежутке
на промежутке 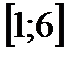 равно
равно
Варианты ответов:
1)  ; 2)
; 2) 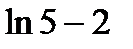 ; 3)
; 3) 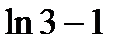 ; 4)
; 4) 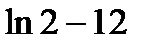 ; 5)
; 5) 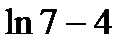 .
.
8. Сумма модулей значений функции 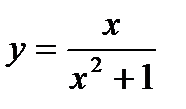 в точках перегиба равна Варианты ответов: 1) 0; 2)
в точках перегиба равна Варианты ответов: 1) 0; 2)  ; 3)
; 3) 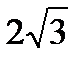 ; 4) 0,75; 5) 18.
; 4) 0,75; 5) 18.
9. Количество целых чисел, принадлежащих промежутку не убывания функции  , равно
, равно
Варианты ответов: 1) 6; 2) 5; 3) 4; 4) 7; 5) бесконечное множество.
10. Функция 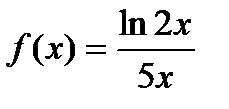 вогнута на промежутке
вогнута на промежутке
Варианты ответов: 1) 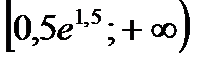 ; 2)
; 2) 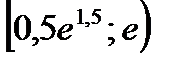 ;
;
3) 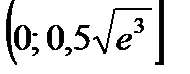 ; 4)
; 4) 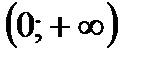 ; 5)
; 5) 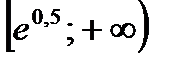 .
.