Задание 12 – это ряд задач из математического анализа на исследование функции: нахождение точек максимума и минимума, а также наибольшего и наименьшего значений функции. При нахождении точек максимума и минимума искомой является абсцисса точки. В случае наибольшего и наименьшего значения функции искомая величина – это значение самой функции в той или иной точке определенного промежутка.
В основном задачи 12 решаются классическим способом — через производную. Но есть такие, в которых производная не считается, и приходится придумывать «нестандартные» подходы.
Задание 12 нельзя назвать трудной задачей, но и легкой ее не назовешь. Конечно, если основательно изучить тему: «Производная функции», знать свойства тех или иных функций, уметь применять определенный алгоритм решения задачи на практике в зависимости от ее условия, то сложностей не возникает. Но как практика показывает, очень много ребят испытывают затруднения при выполнении этого не самого сложного задания.
В связи с этим хотелось бы еще раз обратить внимание на задание 12.
Начнем с простых «классических» примеров.
Пример 1. Найти точку максимума функции 
Начинаем с того, что находим производную этой функции

Приравняем производную к нулю и найдем критические точки
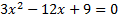
 по теореме Виета найдем корни уравнения
по теореме Виета найдем корни уравнения 
 это и есть, наши критические точки
это и есть, наши критические точки
Определим характер этих точек

|

|

 производной 1 3
производной 1 3
 |
 поведение
поведение
функции
точка  является абсциссой точки максимума функции.
является абсциссой точки максимума функции.
Ответ: 1
Пример 2. Найти наименьшее значение функции  на отрезке
на отрезке 
Алгоритм выполнения точно такой же, как и в предыдущей задаче:
Находим производную

Приравняем производную к нулю и найдем критические точки
 решая данное уравнение, получим корни
решая данное уравнение, получим корни 
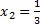
 не входит в указанный промежуток, поэтому в дальнейших вычислениях этот корень не участвует.
не входит в указанный промежуток, поэтому в дальнейших вычислениях этот корень не участвует.
Найдем значение функции в точках  и определим, в какой точке отрезка значение функции будет наименьшим
и определим, в какой точке отрезка значение функции будет наименьшим



Число 17 является наименьшим значением функции на указанном промежутке.
Ответ: 17.
Пример 3. Найти наименьшее значение функции  на промежутке
на промежутке 
И опять все те же самые действия, что и в предшествующих задачах. Особенность данной задачи в том, что производная находится с использованием формулы производной произведения, а также с учетом степени в первом множителе.
 преобразовывая получим
преобразовывая получим
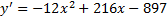 приравняем к нулю, найдем критические точки.
приравняем к нулю, найдем критические точки.



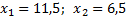 в данном случае оба корня принадлежат к указанному промежутку.
в данном случае оба корня принадлежат к указанному промежутку.
Следующим шагом мы могли бы проверить значение функции в точке 0; 6,5; 11,5 и выбрать интересующее нас значение. Однако, мы сразу узнаем в какой из этих точек значение функции будет наименьшим, для этого определим характер критических точек.
знак
производной
 | |||
 |












 0 6,5 11,5 14
0 6,5 11,5 14
 поведение
поведение
 функции
функции
точка с абсциссой 6,5 является минимумом функции на данном промежутке, следовательно, значение функции в этой точке будет наименьшим.

Ответ: - 245.
Пример 4. Найти наименьшее значение функции  на промежутке
на промежутке 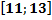





знак
производной
 | |||||
 |  | ||||






 11 12 13
11 12 13
 поведение
поведение
 функции
функции

Ответ: -1
Как видно из приведенных выше примеров, сложность данного задания заключается лишь в нахождении производных различных функций, все остальное подчиняется описанному алгоритму.
Что же делать с функциями, производную, которых найти непросто?
Подобные задания относятся к разряду нестандартных задач и решаются они либо с использованием свойств функций (монотонности, ограниченности периодичности и т.п.) либо используют методы оценки выражений.
Рассмотрим некоторые из приемов решения нестандартных заданий 12 (кстати, данные методы преобразований и исследований функций могут быть полезны при выполнении заданий типа 13-15).
Пример 5. Найдите наименьшее значение функции 
Данная функция является монотонно возрастающей. Следовательно промежутки монотонности функции  совпадают с промежутками монотонности функции
совпадают с промежутками монотонности функции  , т.е. эти функции принимают наименьшее значение в одной и той же точке. Найдем эту точку.
, т.е. эти функции принимают наименьшее значение в одной и той же точке. Найдем эту точку.


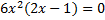

 это значение является наименьшим.
это значение является наименьшим.
Ответ: 243
Пример 6. Найдите наибольшее значение функции 
Рассмотрим функцию  , найдем ее промежутки монотонности.
, найдем ее промежутки монотонности.
 ;
;  ;
;  ;
; 
Определим характер критических точек.
знак
производной
 | |||||
 |  | ||||









 -4 0 4
-4 0 4
 поведение
поведение
 функции
функции


Мы нашли наименьшее и наибольшее значение функции, стоящей в знаменателе аргумента синуса. Логично предположить, что:

учитывая, что функция синуса берется в четной степени и аргумент будет положительным, это неравенство можно записать следующим образом:

Наибольшим значением аргумента будет значение 
(на промежутке  функция синуса возрастает, следовательно все наши предыдущие рассуждения верны)
функция синуса возрастает, следовательно все наши предыдущие рассуждения верны)

Ответ: 0,5625
Пример 7. Найдите наименьшее целое значение функции 
Найдем производную функции, критические точки, и определим их характер.

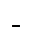

|

|
 производной 0 1,5
производной 0 1,5
 | |||||||
 | |||||||
 | |||||||
| |||||||
 поведение
поведение
функции
Вычислим значение функции в точке минимума 
Число 52 не является наименьшим значением, следовательно наименьшим целым значением функции будет число 53.
Ответ: 53.
Пример 8. Найдите число тех точек, принадлежащих интервалу (-2;3), в которых значение функции  является целым числом.
является целым числом.
Если в некоторой точке значение функции  является целым числом, то и значение функции
является целым числом, то и значение функции  в этой же точке также будет целым числом. Поэтому будем рассматривать функцию
в этой же точке также будет целым числом. Поэтому будем рассматривать функцию 
Найдем ее производную 
Найдем критические точки  ;
; 

Определим поведение функции в окрестностях этих точек
знак
производной



 - + + - + интересующий нас интервал
- + + - + интересующий нас интервал











 -2 0 2
-2 0 2  3
3
поведение
функции
Вычислим ее значения во всех точках заданного интервала





Построим схематичный график этой функции

Функция меняется в промежутке (-128;0]; [0;128]; [117;128]; [117;297) посчитаем количество целых значений функции в этих промежутках
(-128;128] – 255 целых значений;
[117;128] – 11 целых значений;
[117;297) – 179 целых значений.
255+11+179 = 445 количество точек, в которых значение функции является целым числом.
Ответ: 445.
Еще один прием для нахождения наименьшего и наибольшего значения функций, использование различных неравенств, позволяющих оценить заданную функцию.
Например, неравенство Коши для двух чисел 
Пример 9. Найдите наименьшее значение функции 
(данную задачу можно решить и с помощью производной, но ее нахождение займет гораздо больше времени, чем решение через неравенство Коши)
Пусть  ,
, 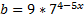 , тогда
, тогда




Сделаем замену  получим следующее неравенство
получим следующее неравенство

Преобразуем  заменяя это неравенство квадратным уравнением, получим корень
заменяя это неравенство квадратным уравнением, получим корень
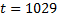
Сделаем обратную замену 

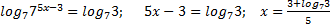 ; мы получили единственную точку, которая является наименьшим значением данной функции (квадратное неравенство, график парабола, ветви направлены вверх, одна точка пересечения с осью абсцисс)
; мы получили единственную точку, которая является наименьшим значением данной функции (квадратное неравенство, график парабола, ветви направлены вверх, одна точка пересечения с осью абсцисс)
Подставим значение этой точки в первоначальную функцию 

Ответ: 1.
Следующий прием решения задач – введение векторов.
Пример 10. Найдите наименьшее значение функции 
Для начала преобразуем подкоренные выражения. Выделим в них полные квадраты.

Используем следующее неравенство

Введем векторы  и
и  с координатами
с координатами  найдем координаты вектора
найдем координаты вектора

 вычислим модули этих векторов
вычислим модули этих векторов 

Т.е  это и есть наименьшее значение данной функции.
это и есть наименьшее значение данной функции.
Ответ: 5.
Пример 11. Найдите наибольшее значение функции 
Используем неравенство, позволяющее оценить сумму синуса и косинуса

Внимательно посмотрев на заданную функцию, можно записать


Тогда 

Заметим, что к правой части неравенства можно еще раз применить подобное преобразование


Получаем, что  , т.е. 5 – это наибольшее значение нашей функции.
, т.е. 5 – это наибольшее значение нашей функции.
Ответ: 5.
Достаточно просто, таким способом, находятся наименьшие и наибольшие значения функций, содержащих переменные под знаком модуля.
Пример 12. Найдите наименьшее значение функции 
Подобное неравенство мы уже использовали 
Найдем ОДЗ функции 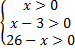
 пусть
пусть 
согласно нашему неравенству


Причем знак равенства выполняется при условии, что



Подставим значение абсциссы точки в функцию
 это и есть наименьшее значение функции на ОДЗ.
это и есть наименьшее значение функции на ОДЗ.
Ответ: 3.
При работе с выражениями, содержащими модули, рационально бывает использовать свойство самого модуля на отдельных промежутках.
Пример 13. Найдите наименьшее значение функции  на отрезке [1;6]
на отрезке [1;6]
Приравняем подмодульные выражения к нулю

 нас интересуют точки, находящиеся внутри отрезка [1;6] – это одно точка 3
нас интересуют точки, находящиеся внутри отрезка [1;6] – это одно точка 3
Проверим значение функции на концах отрезка и в точке 3.
 =3
=3


Наименьшее значение равно -20
Ответ:-20.
Пример 14. Найдите наименьшее значение функции 
Раскроем знак модуля 


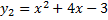




найдем критические точки данных функций и подставим их в исходную функцию.

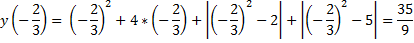


Приведенные мной способы выполнения данных заданий – это лишь часть из множества всевозможных методов и приемов, применяемых для решения подобных задач. Конечно, на уроках мы рассматриваем, чаще всего, стандартные приемы и отрабатываем их на различных видах функций. Но при подготовке более сильных учеников на индивидуальных, факультативных занятиях подобные методы решения, также должны рассматриваться.
Я надеюсь, что задания и примеры их решений подобранные мной, окажутся интересны моим коллегам.
Используемая литература:
ЕГЭ 2013. Математика. Задача B14. Рабочая тетрадь_Шестаков С.А_2013
ЕГЭ 2013. Математика. Типовые тест. задания_под ред. Семенова, Ященко_2013
Математика. ЕГЭ 2013_Книга 1 Мальцев Д.А.
https://kvm.gubkin.ru В.В. Сильвестров «Модуль и производная»