УДК 517.3(075.8)
ISBN 978-5-7782-0820-9 Ó М.Ю. Васильчик, Л.Ф. Колкер,
И.М. Пупышев, О.В. Рязановская, 2007
 Ó Новосибирский государственный
Ó Новосибирский государственный
технический университет, 2007
Предисловие
Данное методическое пособие ставит своей целью помочь студенту самостоятельно овладеть методами решения задач по теме «Интегральное исчисление функций одного переменного». Это определило структуру пособия. В каждом разделе даны краткие теоретические сведения и приведены формулы, необходимые для решения задач, приводится значительное число подробно разобранных примеров. К настоящему времени издано немало превосходных задачников по математическому анализу, и составители не имели своей целью сделать еще один. Ближе всего данное пособие к так называемым «решебникам», в которых даются образцы решения типовых примеров и задач. В пособии практически нет задач повышенной трудности и теоретических задач. Основное внимание авторов сосредоточено на простых, наиболее часто встречающихся типах задач. Авторы надеются, что подробное рассмотрение таких задач позволит студенту самостоятельно или при минимальной помощи преподавателя овладеть основными методами решения задач данного раздела. Это обстоятельство особенно важно для студентов, занимающихся заочно, а также для студентов дневной формы обучения, самостоятельно выполняющих типовые расчеты.
Интегральное исчисление функций одной переменной является базой для решения задач по различным темам математического анализа и специальных разделов высшей математики, таких, к примеру, как обыкновенные дифференциальные уравнения, кратные интегралы, теория поля и другим. В связи с этим в пособии рассмотрены задачи, а также приемы и методы, на которые обычно не хватает учебного времени при прохождении темы «Интегральное исчисление функций одного переменного». Тем самым пособие может быть полезным как своего рода справочник при изучении последующих разделов высшей математики.
Примеров для самостоятельного решения в пособии немного. Они предназначены в основном для самопроверки – достаточно ли усвоены данные методы и приемы. Ко всем примерам в конце каждой главы даны ответы, к некоторым – указания к решению.
Глава 1
НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
§ 1. Непосредственное интегрирование
Пусть на интервале (a, b) определена некоторая функция f (x). Тогда функция F (x), определенная так же на (a, b), называется первообразной функции f (x), если F ¢(x) = f (x) для x 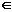 (a, b). Например, функция F (x) = = sin 3 x – первообразная функции f (x) = 3 cos 3 x, а F (x) = x 3 +3 – первообразная f (x) = 3 x 2. Известно, что все первообразные одной функции отличаются друг от друга на постоянное слагаемое. Отсюда следует, что если F (x) – некоторая первообразная функции f (x), то любая другая первообразная Φ(x) имеет вид Φ(х) = F (x) + C, где C – постоянная, зависящая только от Φ.
(a, b). Например, функция F (x) = = sin 3 x – первообразная функции f (x) = 3 cos 3 x, а F (x) = x 3 +3 – первообразная f (x) = 3 x 2. Известно, что все первообразные одной функции отличаются друг от друга на постоянное слагаемое. Отсюда следует, что если F (x) – некоторая первообразная функции f (x), то любая другая первообразная Φ(x) имеет вид Φ(х) = F (x) + C, где C – постоянная, зависящая только от Φ.
Неопределенным интегралом (НИ) от функции f (x) называется множество всех первообразных функции f. Обозначается НИ от f следующим образом: 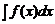 . Таким образом,
. Таким образом,
 .
.
Обычно, следуя традиции, пишут просто
 .
.
Переменная x называется переменной интегрирования, f (x) называется подынтегральной функцией, f (x) dx – подынтегральным выражением. Процесс нахождения неопределенного интеграла от функции f (x) называется интегрированием функции f. Принято говорить также: «Взять интеграл 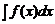 ».
».
Вычисление НИ есть в определенном смысле операция, обратная к нахождению дифференциала функции. Действительно, пусть F (x) –первообразная функции f (x). Тогда  = d (F (x) + C) = F ’(x) dx = = f (x) dx. С другой стороны,
= d (F (x) + C) = F ’(x) dx = = f (x) dx. С другой стороны,
 =
=  =
= 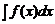 = F (x) + C.
= F (x) + C.
Отсюда вытекает, что из таблицы производных основных элементарных функций можно получить таблицу интегралов от основных элементарных функций. Эти интегралы называются табличными. Приведем здесь таблицу этих интегралов.
1. 
2. 
3.  ,
, 
4. 
5. 
6. 
7. 
8. 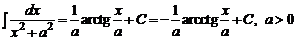 .
.
9.  .
.
10. 
11. 
Вычисление НИ в основном заключается в сведении его к табличному интегралу. Достигается это с помощью свойства линейности НИ, а также с помощью некоторых приемов, о которых речь будет ниже. Необходимо отметить, что в то время как, используя правила дифференцирования, можно вычислить производную любой элементарной функции, и эта производная снова будет элементарной функцией, неопределенный интеграл от элементарной функции может оказаться неэлементарной функцией. В этом случае говорят, что интеграл «не берется» и называют его «неберущимся». Таковы, например, интегралы 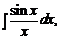
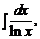
 и др. В связи с этим становится очевидным, что необходимо хорошо знать основные классы функций, для которых НИ являются элементарными функциями («берущиеся» интегралы), и, решая примеры, хорошо освоить основные методы интегрирования.
и др. В связи с этим становится очевидным, что необходимо хорошо знать основные классы функций, для которых НИ являются элементарными функциями («берущиеся» интегралы), и, решая примеры, хорошо освоить основные методы интегрирования.
Напомним свойство линейности НИ. Пусть А и В – постоянные. Тогда справедливо равенство

Это свойство обобщается на любое число слагаемых. Пусть  – некоторые функции, C
– некоторые функции, C  , …, C
, …, C  – постоянные. Тогда верно равенство
– постоянные. Тогда верно равенство
 .
.
Вычисление НИ, использующее только линейное свойство НИ, табличные интегралы и легко проверяемую формулу
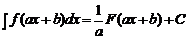 , (1)
, (1)
где F – первообразная f, называют непосредственным интегрированием.
Рассмотрим примеры. Вычислить следующие интегралы.
1.1. 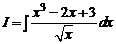 .
.
1.2. 
1.3. I = 
Решение.
1.1. Поделив числитель на знаменатель почленно, получим

1.2. Представим числитель в виде  и поделим числитель на знаменатель почленно. Получаем
и поделим числитель на знаменатель почленно. Получаем

1.3. Используя свойство линейности интеграла и формулу (1), запишем

При вычислении интегралов от выражений, состоящих из тригонометрических функций, полезны следующие формулы:
sin α x cos β x = 
sin α x sin β x = 
cos α x cos β x = 
cos 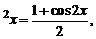 sin
sin  1 + tg
1 + tg 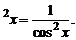
Рассмотрим примеры.
1.4. 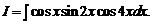
Решение. Преобразуем подынтегральную функцию следующим образом:
сos x sin 2 x ·cos 4 x =  (sin x + sin 3 x) cos 4 x =
(sin x + sin 3 x) cos 4 x =
=  (–sin 3 x + sin 5 x – sin x + sin 7 x).
(–sin 3 x + sin 5 x – sin x + sin 7 x).
Тогда

1.5. 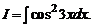
Решение. Используя тригонометрическую формулу 
 , преобразуем подынтегральную функцию и вычисляем интеграл
, преобразуем подынтегральную функцию и вычисляем интеграл

1.6. I = 
Решение. Преобразуем подынтегральную функцию, используя формулу  , а затем, применяя аналогичную формулу к
, а затем, применяя аналогичную формулу к  , вычисляем интеграл
, вычисляем интеграл


= 
Задачи для самостоятельного решения
Вычислить следующие интегралы.
1.7.  1.8.
1.8. 
1.9. 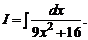 1.10.
1.10. 
1.11. I =  1.12. I =
1.12. I = 
1.13. 
§ 2. Замена переменной в неопределенном интеграле
Часто при вычислении НИ очень полезным оказывается переход к новой переменной или, как иногда говорят, метод подстановки. Пусть функция x = φ(t) определена и дифференцируема на некотором интервале (ά, β) и пусть Х – множество значений этой функции – интервал, полуинтервал или отрезок. Пусть на Х определена функция f (x). Тогда, если на множестве Х функция f (x) имеет первообразную, то на интервале (α, β) справедлива формула замены переменной в НИ:

Рассмотрим пример.
2.1. 
Решение. Сделаем в интеграле замену переменной x – 3 = t и вычислим интеграл


В приведенных выкладках вертикальными черточками отделены вспомогательные рассуждения. Это позволяет не прерывать цепочку выкладок. Далее такая форма записи вычислений будет использоваться систематически.
Рассмотрим несколько примеров.
2.2.  .
.
Решение. Делая тригонометрическую подстановку, вычисляем интеграл





= 
2.3. 
Решение. Делая замену переменной, вычисляем


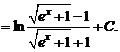
2.4. 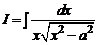 .
.
Решение. Будем считать, что x > a > 0. Как правило, неопределенный интеграл можно вычислить несколькими способами. Вычислим интеграл этого примера двумя способами.
А. Домножим числитель и знаменатель подынтегральной дроби на x и сделаем замену переменной. Получим


Б. Вынесем  из-под корня и сделаем замену переменной
из-под корня и сделаем замену переменной


Вид получившейся первообразной отличен от вида первообразной, полученной в случае А. Но если обозначить arccos  то
то 
 . Тогда
. Тогда

Следовательно, в обоих случаях первообразной является одна функция.
2.5. 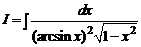 .
.
Решение. Делая замену переменной, вычисляем


Отметим некоторые типичные случаи применения замены переменной. Рассмотрим сначала следующий интеграл:

после замены  . В частности, при a = 2 имеем
. В частности, при a = 2 имеем

Рассмотрим пример, который понадобится нам в дальнейшем.
2.6.  .
.
Решение. В этом примере  . Делая замену переменной, получаем
. Делая замену переменной, получаем

 ,
,

Часто встречаются также следующие подстановки:




2.7. 
2.8. 

Задачи для самостоятельного решения
Вычислить интегралы.
2.9.  2.10.
2.10. 
2.11. 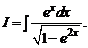 2.12.
2.12. 
2.13. 
§ 3. Интегрирование по частям
Пусть u и v – дифференцируемые функции. Формулой интегрирования по частям называется формула
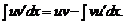
Поскольку  , то формулу интегрирования по частям можно записать в более простом виде
, то формулу интегрирования по частям можно записать в более простом виде
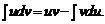
Интегрирование по частям чаще всего применяется тогда, когда производная  является «более простой», чем сама функция u. При этом, естественно, функция v должна относительно просто находиться по заданному дифференциалу
является «более простой», чем сама функция u. При этом, естественно, функция v должна относительно просто находиться по заданному дифференциалу 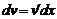 .
.
Рассмотрим примеры.
3.1. 
Решение. За функцию u в этом примере естественно принять u =
= x – 1, так как du = dx. Вычисляем интеграл.

3.2. 
Решение. Здесь мы однозначно решаем, что u = arctg x. Применяя формулу интегрирования по частям, вычисляем
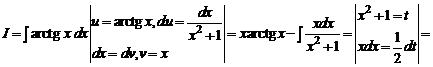

Интегрированием по частям можно вычислить интегралы:




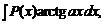
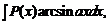
 ,
,
где  многочлен, и многие другие. Действительно, рассмотрим, например, интеграл
многочлен, и многие другие. Действительно, рассмотрим, например, интеграл 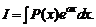 Если положить u = P (x),
Если положить u = P (x),  , то согласно формуле интегрирования по частям получаем
, то согласно формуле интегрирования по частям получаем

Мы получаем интеграл того же вида, что и первоначальный, но теперь многочлен  имеет степень меньшую, чем у многочлена
имеет степень меньшую, чем у многочлена  . Далее можно снова применить формулу интегрирования по частям, затем еще раз и далее, пока не придем к табличному интегралу
. Далее можно снова применить формулу интегрирования по частям, затем еще раз и далее, пока не придем к табличному интегралу  К интегралам вида
К интегралам вида  сводятся интегралы вида
сводятся интегралы вида  Действительно, после замены переменной
Действительно, после замены переменной 
 , получаем
, получаем
 .
.
В интегралах, содержащих обратную тригонометрическую функцию, за функцию u следует брать эту функцию.
Рассмотрим примеры.
3.3. 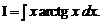
Решение. Положим u = arctg x, x dx = dv. Тогда

Применяя формулу интегрирования по частям, вычисляем



3.4. 
Решение. В этом примере 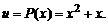 Берем интеграл по
Берем интеграл по
частям:



3.5. 
Решение. Сначала преобразуем подынтегральную функцию, затем сделаем замену переменной:

 .
.
Теперь применяем формулу интегрирования по частям:


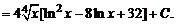
3.6. 
Решение. Этот интеграл можно вычислить разными способами. Можно, например, сделать тригонометрическую подстановку x = a tg t или гиперболическую (гиперболические функции мы рассмотрим дальше) x = a sh t. Мы возьмем этот интеграл по частям. Сначала преобразуем подынтегральную функцию:


Обозначим интеграл в правой части через  и вычислим его интегрированием по частям:
и вычислим его интегрированием по частям:

Таким образом,
 .
.
Решая это уравнение относительно 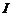 , находим
, находим

3.7. 
Решение. Мы вычислим этот интеграл с помощью повторного применения формулы интегрирования по частям, получив простое уравнение для нахождения исходного интеграла:


Таким образом, мы приходим к уравнению
 .
.
Решая это уравнение относительно  , находим
, находим

3.8. Аналогично вычисляется интеграл
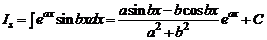 .
.
К интегралам  и
и  приводятся после замены переменной интегралы
приводятся после замены переменной интегралы  и
и  Действительно, сделав замену переменной ln x = t,
Действительно, сделав замену переменной ln x = t, 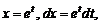 получим
получим
3.9. 

Аналогично вычисляется интеграл
3.10. 
Используя интегралы из примеров 3.7 и 3.8 и формулу интегрирования по частям, можно вычислять интегралы вида  и
и  .
.
3.11. 
Решение. Используя интегралы из примеров 3.7 и 3.8 и формулу интегрирования по частям, вычисляем наш интеграл

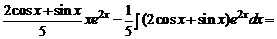

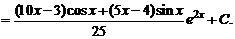
Одним из применений метода интегрирования по частям является вывод рекуррентных формул. В этих формулах интегралы, зависящие от индекса n > 0 (n  N), выражаются через интегралы того же типа с меньшими индексами.
N), выражаются через интегралы того же типа с меньшими индексами.
Рассмотрим несколько примеров.
3.12. 
Решение. Сначала преобразуем подынтегральную функцию:

Интеграл в правой части преобразуем с помощью формулы интегрирования по частям:


Для нахождения функции v мы воспользовались примером 2.6. Таким образом, мы получаем

 .
.
Отсюда следует рекуррентная формула


Так как при n = 1

то при n = 2 получаем


При n = 3 имеем


и т. д.
Используя метод интегрирования по частям, можно получить следующие рекуррентные формулы:
3.13.  .
.
3.14.  .
.
3.15.  .
.
Покажем, как выводится формула из примера 3.13. Вывод формул из примеров 3.14 и 3.15 оставляем читателям.
Решение. Применяем формулу интегрирования по частям, полагая  dx = dv. Тогда
dx = dv. Тогда
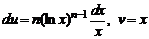
и 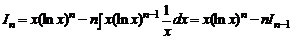 .
.
Рассмотрим еще один пример.
3.16. 
Решение. Применим сначала формулу интегрирования по частям, а затем произведем несложные преобразования подынтегральной функции:



Приведя подобные члены, отсюда получаем
(2β + 1) I  I
I 


Например, так как

то


и т.д.
Интегрированием по частям выводятся рекуррентные формулы для интегралов 

 и многие другие.
и многие другие.
При вычислении некоторых интегралов приходится применять формулу интегрирования по частям несколько раз. В таких случаях часто удобнее применять обобщенную формулу интегрирования по частям:

где

Особенно удобна формула, когда u = P (x) – многочлен степени n.
3.17. 
Решение. Пусть  Тогда
Тогда 
 Вычисляем далее
Вычисляем далее

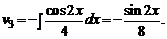
Применяя теперь обобщенную формулу интегрирования по частям, находим интеграл


Задачи для самостоятельного решения
Вычислить интегралы из примеров 3.18 и 3.23.
3.18.  3.19.
3.19. 
3.20.  3.21.
3.21. 
3.22.  3.23.
3.23. 
§ 4. Интегралы 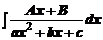 и
и 
Рассмотрим вначале интеграл  Выделим полный квадрат в знаменателе подынтегральной дроби:
Выделим полный квадрат в знаменателе подынтегральной дроби:

Обозначим через D дискриминант квадратного трехчлена, 
Если D < 0, то
 .
.
Сделаем замену переменной  . Тогда
. Тогда

Если D > 0, то
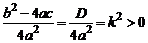 ,
,
и тогда
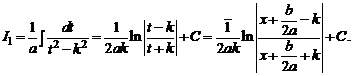
Рассмотрим теперь интеграл

Если сделать замену  то мы видим, что при A = 2 a, B = b мы имели бы
то мы видим, что при A = 2 a, B = b мы имели бы

Если это не так, то мы сведем вычисление интеграла I к вычислению такого интеграла и интеграла  , рассмотренного выше. Подберем числа M и N так, чтобы для всех x выполнялось Ax + B = M (2 ax + b) + N. Легко видеть, что
, рассмотренного выше. Подберем числа M и N так, чтобы для всех x выполнялось Ax + B = M (2 ax + b) + N. Легко видеть, что 
 Таким образом,
Таким образом,

Первый интеграл в правой части равен ln  а второй – это интеграл
а второй – это интеграл  .
.
Рассмотрим интеграл

Выделим под корнем полный квадрат и перепишем интеграл в виде

Пусть a > 0. Сделаем замену переменной  тогда получим
тогда получим


Если a < 0, то – a > 0 и мы получаем
 ,
,

Если D < 0, то под корнем – отрицательная величина. Следовательно, при a < 0 необходимо выполняется  . Полагая
. Полагая  (k > 0), получаем
(k > 0), получаем

Для интеграла

подбираем, как мы это делали ранее, числа M и N таким образом, чтобы выполнялось Ax + B = M (2 ax + b) + N. Тогда интеграл I запишется в виде
 .
.
Первый интеграл берется заменой 


Второй интеграл – это интеграл  , рассмотренный выше.
, рассмотренный выше.
Замечание. В интеграле

можно сразу выделить полный квадрат и сделать замену переменной  и получить
и получить 
 .
.
Первый интеграл равен  Второй зависит от знака D. Если D < 0, то, полагая
Второй зависит от знака D. Если D < 0, то, полагая  (k > 0), имеем
(k > 0), имеем

Если D > 0, то полагая  (
( > 0), получим
> 0), получим

Аналогично можно рассмотреть интеграл

Рассмотрим примеры.
4.1. 
Решение. Так как d (2 x 2 – 3 x + 3) = (4 x – 3) dx, то подберем числа M и N из условия x + 2 = M (4 x – 3) + N. Тогда M = 1/4, 2 + 3/4 = N = 11/4. Отсюда следует




4.2. 
Решение. Выделим полный квадрат в знаменателе и сделаем замену переменных:

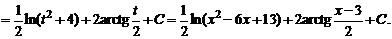
4.3. 
Решение. Если положить 5 + x – x 2 = t то dt = (–2 x + 1) dx. Найдем числа M и N из равенства x = M (–2 x + 1) + N. Получаем M = –1/2,
N = 1/2. Тогда


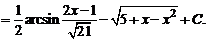
4.4. 
Решение. Выделим под корнем полный квадрат и сделаем замену переменной:



Задачи для самостоятельного решения
Вычислить интегралы из примеров 4.5 – 4.10.
4.5.  4.6.
4.6. 
4.7.  4.8.
4.8. 
4.9. 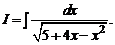 4.10.
4.10. 
§ 5. Интегрирование рациональных функций
Рациональной функцией называется функция вида  где P (x) и Q (x) – многочлены. Если степень многочлена P меньше степени Q, то функция
где P (x) и Q (x) – многочлены. Если степень многочлена P меньше степени Q, то функция  называется правильной рациональной дробью. Интегрирование рациональной функции производится по следующей схеме.
называется правильной рациональной дробью. Интегрирование рациональной функции производится по следующей схеме.
1. если степень P больше или равна степени Q, то надо выделить целую часть, т.е. представить дробь  в виде
в виде
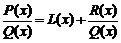 ,
,
где L и R – многочлены, причем степень R строго меньше степени Q. Это можно сделать, поделив P на Q «столбиком», как делят числа.
2. разложить знаменатель Q на простейшие действительные множители
Q (x) =  ,
,
причем участвующие в разложении двучлены и трехчлены различны и трехчлены не имеют действительных корней.
3. Правильную рациональную дробь  представить в виде суммы простых дробей
представить в виде суммы простых дробей


 ,
,
где  – некоторые действительные постоянные, подлежащие определению. Для их нахождения дроби в правой части равенства приводят к общему знаменателю и затем приравнивают R (x) к числителю получившейся дроби. Известно, что если два многочлена равны, то коэффициенты при одинаковых степенях переменной также равны. Приравняв коэффициенты, получаем систему линейных уравнений, в которой уравнений столько же, сколько и неизвестных. Решая систему (например, методом Гаусса), находим неизвестные коэффициенты. Можно находить коэффициенты, придавая переменной x конкретные значения, получая тем самым уравнения для коэффициентов. Часто, придавая переменной специально подобранные значения, сразу получаем некоторые коэффициенты. Иногда это позволяет найти все коэффициенты, иногда – часть их. Можно подстановкой найти часть коэффициентов, а для оставшихся получится система уравнений с меньшим числом уравнений.
– некоторые действительные постоянные, подлежащие определению. Для их нахождения дроби в правой части равенства приводят к общему знаменателю и затем приравнивают R (x) к числителю получившейся дроби. Известно, что если два многочлена равны, то коэффициенты при одинаковых степенях переменной также равны. Приравняв коэффициенты, получаем систему линейных уравнений, в которой уравнений столько же, сколько и неизвестных. Решая систему (например, методом Гаусса), находим неизвестные коэффициенты. Можно находить коэффициенты, придавая переменной x конкретные значения, получая тем самым уравнения для коэффициентов. Часто, придавая переменной специально подобранные значения, сразу получаем некоторые коэффициенты. Иногда это позволяет найти все коэффициенты, иногда – часть их. Можно подстановкой найти часть коэффициентов, а для оставшихся получится система уравнений с меньшим числом уравнений.
4. После нахождения коэффициентов для интегрирования дроби  остается найти интегралы от дробей следующего вида:
остается найти интегралы от дробей следующего вида:

Первые две дроби дают табличные интегралы. Интегрирование третьей дроби разобрано в предыдущем параграфе. Интегрирование четвертой дроби после замены переменной сводится к вычислению уже разобранных интегралов. Действительно,


Первый интеграл разобран в примере 2.6, второй – в примере 3.12.
Замечание. При разложении правильной рациональной дроби на простейшие часто встречаются следующие разложения:
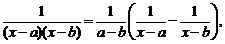



Рассмотрим примеры.
5.1. 
Решение. Поскольку степень числителя больше степени знаменателя, вначале поделим числитель на знаменатель «столбиком»:
 _
_ 



_ 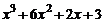


Таким