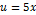Электронный конспект лекций по
«Интегральному исчислению функций одной и многих переменных»
(Математический анализ 2 семестр)
Направление подготовки
Информационная безопасность телекоммуникационных систем»
Специализация
Разработка защищенных телекоммуникационных систем»
Квалификация выпускника
Специалист
Форма обучения
Очная
Москва 2017
Оглавление
Лекция 1. 3
Лекция 2. 7
Лекция 3. 11
Лекция 4. 15
Лекция 5. 19
Лекция 6. 24
Лекция 7. 27
Лекция 8. 31
Лекция 9. 34
Лекция 10. 35
Лекция 11. 38
Лекция 12. 41
Лекция 13. 47
Лекция 14. 51
Лекция 15. 54
Список вопросов к экзамену. 58
Образец билета. 60
Список литературы.. 61
Лекция 1
Первообразная и неопределенный интеграл
Курс состоит из 3х глав:
1 глава Интегральное исчисление функции одной переменной
2 глава Интегральное исчисление функции многих переменных
3 глава Элементы теории поля
До сих пор (в 1ом семестре решалась) Теперь решаем
Прямая задачаОбратную задачу
Дан: путь F(х) Дана: f(x)=F′ (x)
Найти: f(x)=F′(x)-мгновенную скорость. Найти: F(x)-путь
| F(x) Рис. 1 |
| f(x) |
2)Каким аппаратом находится F(x)?
О.1 (Первообразной)
F(x)-первообразная для f(x) на промежутке (X) 
F’(x)=f(x) ∀xϵX (1)
П.1 f(x)=sin(x); cos(x); e-x; 
F(x)=-cos(x); sin(x); -e-x; tg(x)
Т.1 (О множестве всех первообразных)
Если F(x) – первообразная для f(x) на Х, то
1) F(x)+C –также первообразная для f(x) на Х, где С-произвольная постоянная.
2) для ∀Ф(х), первообразной для f(x) на Х, выполняется Ф(х)=F(x) + С (2)
Доказательство
1) Очевидно, т.к. (F(x)+C)’=F’(x)=f(x), ∀xϵX
2) Рассмотрим разность Ф(х)-F(x) и возьмем от нее производную
(Ф(х)-F(x))’= Ф’(х)-F’(x)=f(x)-f(x)=0, ∀xϵX => Ф(х)-F(x)=C, ∀xϵX
Замечание1.
Теорема 1 дала ответ на 1ый вопрос: решая обратную задачу мы получаем множество(семейство) путей, отстоящих друг от друга на произвольную константу С(рис.2)
О.2 (Неопределенного интеграла)
| f(x) Ф(х) F(x) Рис. 2 |
интегралом и обозначается: 
(3)
f(x)dx –подынтегральное выражение;
f(x)-подынтегральная функция;
x-переменная интегрирования.
Замечание 2.
Введением определения 2 получили ответ на 2-ой вопрос: множество путей
находится действием интегрирования.
П.1 Теперь можно записать так:
; 
; 
;
= tgx +c
Свойство неопределенного интеграла
1. 
(доказательство очевидно)
2. d(
-подынтегральное выражение (доказательство очевидно)
2′.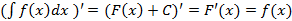 
– подынтегральная функция (доказательство очевидно)
Замечание 3
1) Если интегральное равенство верно, то при его дифференцировании должна получиться подынтегральная функция. На этом основано доказательство таблицы интегралов
2) Как показывают свойства 1,2,2’, действия интегрирования и дифференцирования взаимно обратные.
3. Свойство линейности
= 
+ 
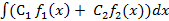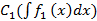| Св 2’ |
Возьмем производную от правой части
]’= 
+ 
= С1f1(x)+C2f2(x) - подынтегральная
функция левой части свойства линейности. Следовательно, свойство линейности верно.
Замечание 4
Свойство линейности справедливо для любого конечного числа слагаемых функций
П.2
– применили свойство линейности для 3-х слагаемых и известные из П.1 интегралы)
Перейдем к выводу таблицы интегралов, используя для доказательства свойство 2′. Для лучшего понимания и запоминания таблицы приведем ее вместе с таблицей производных.
| Таблица производных | Таблица интегралов | Вывод | |
| (С)′=0 | 
| (С)′=0-подынтегральная ф. | |
| (x)′=1 | 
| (x+C)′=1 | |
(
| 
|  = 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
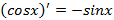
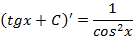
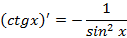
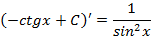
| очевидно | |
| 
| очевидно | |
| 
| очевидно | |
| 
| очевидно | |
| 
| очевидно | |
| 
| очевидно | |
| Взять производную от правой части и получить подынтегральную функцию самостоятельно | ||
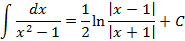
| Проверить так же, как в 16. |
Т.2 (Об инвариантности формул интегрирования)
Всякая формула интегрирования сохраняет свой вид при подстановке вместо переменной любой дифференцируемой функции от неё, т.е. если 
| Инв. Св.1 1го дифф. |
При доказательстве использовали инвариантность 1го дифференциала:
и свойство 1 неопределенного интеграла.
Замечание 5.
Благодаря теореме 2, можно расширить таблицу интегралов. Пусть 
. ф.
| Расширенная таблица |
| ||
|
| ||
|
| ||
|
| ||
|
| ||
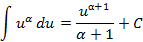
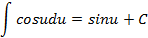
| u=3x+1
| ||
|
| ||
|
|
Задание 1 на дом: 1)Продолжить расширенную таблицу и придумать примеры.
2)Внести в таблицу и запомнить 
Замечание 6
Теорема 2 остается справедливой, если делается подстановка 
.
Т.3 (Интегрирование по частям)
Пусть 
- непрерывно-дифференцируемые функции, тогда имеет место формула:
(4)
Доказательство проведем, используя свойство 2. Возьмем дифференциал от правой части (4)
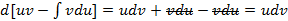-подынтегральное выражение левой части(4), ч.т.д.
По частям берутся следующие интегралы:
| u dv u dv dv u dv u dv u dv |
; 
; 
; 
; 
;
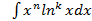Интегралы 
–дважды интегрированием по частям сводятся к алгебраическому уравнение относительно искомого I.
Задание на дом2
1) Вывести рекуррентное соотношение:
, где 
; (5)
Здесь 
Лекция 2
Интегрирование некоторых классов функций
1. Интегрирование дробно-рациональных функций
О.3 (Простейших дробей)
Дроби вида:
1) 
; 2) 
; 3) 
; 4) 
, где 
не имеет действительных корней т.е.:
.
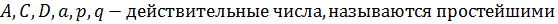
Т.4 (об интегрировании простейших дробей)
Простейшие дроби интегрируются в элементарных функциях
Доказательство (конструктивное)
1. 
A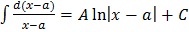 
2. 
3. 
| 
|
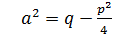
4. Задание на дом:
Показать, используя рекуррентное соотношение предыдущей лекции, что интегрирование дробей 4-го типа приводит к алгебраической сумме логарифма, степенной функции и обратной тригонометрической функции.
О.4 (дробно-рациональной функции)
Дробно-рациональной функцией называется отношение 
многочленов
, причем (2)
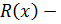правильная дробь при 
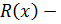; неправильная дробь при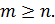 
Теорема 5 (о разложении правильной дроби на сумму простейших дробей).
(б.д.) Любая правильная дробь , со знаменателем 
… 
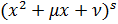, где (3)
(4)
может быть представлена в виде суммы конечного числа простейших дробей:
(5)
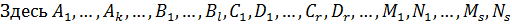– неопределенные коэффициенты.
Т.6 Любая дробно-рациональная функция интегрируема в элементарных функциях.
Доказательство
1. , очевидно получается при использовании теорем 5 и 4.
выделяем целую часть (многочлен или константу) делением 
на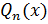 
плюс правильную дробь; далее используем свойство линейности неопределенного интеграла и теоремы 5 и 4.
Замечание 1. Неопределенные коэффициенты могут быть найдены 3-мя способами
1. Методом частных значений (особенно целесообразно, когда все корни знаменателя действительные, простые);
2. Составлением систем уравнений относительно искомых коэффициентов;
3. Комбинированным способом.
П.1
2x-1= 
|
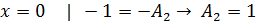
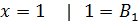
2. Интегрирование тригонометрических функций (рациональных функций от тригонометрических)
О.5 Рациональной функцией от 
называется функция, в которую входят в целых степенях; обозначение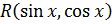 
П.2 
Т.7 Интегрирование рациональной функции от 
сводится к интегрированию дробно-рациональной функции, т.е.
(6)
Доказательство
| 
| 
|
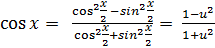
Подставим эти выражения в исходный интеграл
П.3
3. Интегрирование некоторых классов иррациональных функций
Т.8 Интегралы от иррациональных функций, представленных ниже, с помощью тригонометрических подстановок берутся в элементарных функциях
Доказательство (конструктивное)
1. 
– элементарная функция
(или x=acos t)
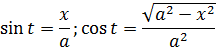
2. 
– (*)
здесь использована формула интегрирования по частям;
(или 
)
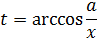
Задание на дом: в выражении (*) перейти к старой переменной самостоятельно.
3. 
x=atg t (x=actg t)
Задание на дом: провести вычисления самостоятельно.
Лекция 3
Определенный интеграл
Задача о площади криволинейной трапеции
Определение 6 (Криволинейной трапеции)
сверху, с боков прямыми 
и 
; снизу осью 
называется криволинейной трапецией (рис.3)
| x |
Рис.3 – Криволинейная трапеция
Определение 7 (Площади криволинейной трапеции)
Рассмотрим разбиение 
отрезка 
на 
частей:
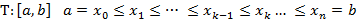
Составим n-ступенчатую фигуру и рассмотрим ее площадь (рис.4):
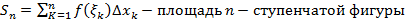(1)
| x |
|
|
|
|
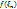
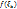
Рис. 4 – n-ступенчатая фигура
Площадью S криволинейной трапеции называется предел площади n-ступенчатой фигуры при
Замечание 1
Решение задачи о площади криволинейной трапеции привело к понятию определенного интеграла Римана (немецкий математик 19в.)
Общая постановка
Рассмотрим разбиение отрезка на произвольных частей. Составим формально:
Определение 8 (интегральной суммы Римана)
Выражение (сумма) вида (3) называется интегральной суммой Римана.
Вопрос 1
От каких факторов зависит сумма Римана?
Ответ:
1) От y=f(x);
2) ;
3) от способа разбиения 
4) от выбора точек 
Вопрос 2
Сколько интегральных сумм можно составить для заданных 
?
Ответ
Бесчисленное множество
Определение 9 (Определенного интеграла Римана)
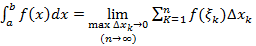
Замечание 2
В ходе предельного перехода пропадает зависимость результата от (3) и (4) факторов; в (4) а-нижний предел, b – верхний предел интегрирования
Теорема 9 (о существовании определенного интеграла y непрерывной функции)
(б.д.)
Определение 10 (интегрируемой функции)
Замечание 3
Теорема 9 утверждает, что непрерывные на [a,b] функции интегрируемы на нем
Теорема 10 (об интегрировании кусочно-непрерывной функции)
Кусочно-непрерывные на [a,b] функции (т.е функции, имеющие конечное число точек разрыва первого рода) интегрируемы на этом отрезке
Доказательство
Станет очевидным после свойства аддитивности определенного интеграла
Геометрический смысл определенного интеграла
Пример 1
