1. Линейность (это свойство справедливо для любого конечного числа слагаемых функций)

2. При перестановке пределов интегрирования знак интеграла меняется на противоположный
Доказательство становится очевидным, если рассмотреть разбиения



|
3. Свойство аддитивности
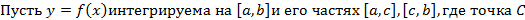

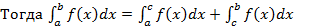

Доказательство
| рис. 6а |
а  b b
|
 ;
;


| рис. 6б |
а  c c
|
Тогда 
4. Интегрирование неравенств
Пусть 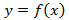 интегрируема на
интегрируема на 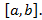 При интегрировании неравенств знак неравенств сохраняется, т.е.
При интегрировании неравенств знак неравенств сохраняется, т.е.




Доказательство


5. Оценка интеграла
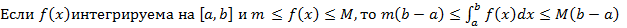

Доказательство очевидно вытекает из свойства (4) и равенства (6)
Замечание 4

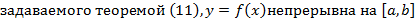
Теорема 11 (о среднем)

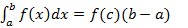 (12)
(12)
| Рис 7 – Геометрический смысл теоремы о среднем |

|
| x |
| f(c) |
Доказательство
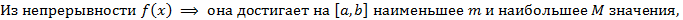

Определение 11(средне-арифметического)
Средне-арифметическим непрерывной функции называется
 (13)
(13)
Замечание 5.
Теорема 11 утверждает, что yср=f(c).
Геометрический смысл теоремы о среднем
Для непрерывной на [a,b] функции внутри (a,b) найдется точка c такая, что площадь криволинейной трапеции будет равна площади прямоугольника с высотой f(с) и основанием, равным (b-a). (см. рис. 7)
Лекция 4
Интеграл с переменным верхним пределом. Теорема Ньютона-Лейбница. Замена переменной в определенном интеграле. Формула интегрирования по частям в определенном интеграле.
Определение 14 (интеграла с переменным верхним пределом)
Пусть y = f(x) интегрируема на  .
.
Тогда 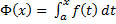 - интеграл с переменным верхним пределом, t – переменная (1) интегрирования
- интеграл с переменным верхним пределом, t – переменная (1) интегрирования

|
| b |
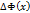
|
| a |
| y |
| x |
 :
:
 - переменная площадь криволинейной трапеции
- переменная площадь криволинейной трапеции
| . с |
Рис. 8  – переменная площадь
криволинейной трапеции – переменная площадь
криволинейной трапеции
|
| x |

|
Замечание 1:
Изучение интегралов с переменным нижним пределом
| (2) |

Замечание 2: 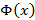 – это функция, следовательно, можно говорить о еенепрерывности и дифференцируемости.
– это функция, следовательно, можно говорить о еенепрерывности и дифференцируемости.
Теорема 12: (О непрерывности интеграла с переменным верхним пределом)
Если  – непрерывна на
– непрерывна на  , то
, то 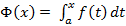 также непрерывна на
также непрерывна на  ; т.е.
; т.е.

Доказательство:

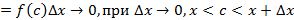 ; (см. Рис. 8). (3)
; (см. Рис. 8). (3)
Из (3) вытекает по определению непрерывности на языке приращений, что 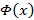 – непрерывна
– непрерывна 
Теорема 13: (О дифференцируемости интеграла с переменным верхним пределом)
Для  , непрерывной на
, непрерывной на 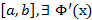 и она равна подинтегральной функции, взятой в верхнем пределе; т.е.
и она равна подинтегральной функции, взятой в верхнем пределе; т.е.

Доказательство:
Составим формально  , т.к. точка c:
, т.к. точка c: 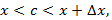
 Ч.Т.Д.
Ч.Т.Д.
Замечание 3:
Из теоремы 13 вытекает, что интеграл с переменным верхним пределом  является первообразной своей подынтегральной функции
является первообразной своей подынтегральной функции 
Поэтому теорему 13 еще называют теоремой существования первообразной у непрерывной функции:
Теорема 14:
Если  непрерывна на
непрерывна на  , то у нее на одном отрезке
, то у нее на одном отрезке  первообразная.
первообразная.
Замечание 4:
Теоремы 13 и 14 входят в экзаменационные билеты со своими формулировками, хотя, на самом деле, это две разные формулировки одной и той же теоремы – 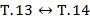
| (5) |

Замечание 5:
Формулу (5) можно переписать так 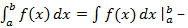 связь интегралов (6)
связь интегралов (6)
Символ  обладает свойством линейности.
обладает свойством линейности.
В равенстве (6) наглядно видна связь определенного интеграла и неопределенного интеграла. Исторически Ньютон шел к введению неопределенного интеграла от физической задачи нахождения пути материальной точки по известной мгновенной скорости, а Лейбниц – от геометрической задачи нахождения площади криволинейной трапеции; решая ее он пришел к понятию определенного интеграла.
Доказательство теоремы Ньютона-Лейбница
Пусть 
Тогда при 
 Ч.Т.Д.
Ч.Т.Д.
Методы вычисления определенных интегралов
1. >
| y |
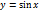
|
 (кв. ед.) –
(кв. ед.) –
| x |
| Рис. 9 |

|
Пример 2:
| y |
 (кв. ед.) –
(кв. ед.) –
| x |
| Рис. 10 |
2. Интегрирование по частям в определенном интеграле
Теорема 16:
Если 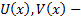 непрерывно дифференцируемы
непрерывно дифференцируемы
на  , то
, то  (7)
(7)
Доказательство:
Становится очевидным при использовании формулы (6) и формулы интегрирования по частям в неопределенном интеграле, а также свойства линейности символа 
 Ч.Т.Д.
Ч.Т.Д.
Пример 3:

3. Замена переменной в определенном интеграле
Теорема 17: (О замене переменной в определенном интеграле)

Замечание 6:
Теорема 17 утверждает, что при замене переменной интегрирования (т.е. при подстановке) в определенном интеграле не надо возвращаться к старой переменной, а целесообразно поменять пределы интегрирования
Пример 4:


Доказательство теоремы 17:
Применяя теорему Ньютона-Лейбница запишем левую часть формулы (8)
 (9)
(9)
Преобразуем правую часть равенства (8):

 (10)
(10)
Сравнение правых частей равенств (9) и (10) доказывает нужное нам равенство (8).
Замечание 7:
Нарушение хотя бы одного из условий теоремы Ньютона-Лейбница ведет к понятиям несобственных интегралов. Если же оба условия теоремы выполняются, то такие интегралы называются собственными.
Пример 5:
a)  – собственный, т.к. 1)
– собственный, т.к. 1) 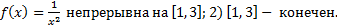
b)  – несобственный интеграл, т.к.
– несобственный интеграл, т.к.  в нижнем конце (x=0) терпит разрыв 2-го рода, не выполняется условие теоремы Ньютона-Лейбница. Применять ее нельзя!
в нижнем конце (x=0) терпит разрыв 2-го рода, не выполняется условие теоремы Ньютона-Лейбница. Применять ее нельзя!
На следующей лекции изучим несобственные интегралы
Замечание 8:
Благодаря Теореме 17 для вычисления определенных интегралов будем использоваться все подстановки, изученные для неопределенных интегралов.
Лекция 5
Несобственные интегралы
О.13 (Собственных и несобственных интегралов)
Если для 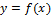 и
и  выполняются оба условия т. Н.-Л., то такие интегралы называют собственными.
выполняются оба условия т. Н.-Л., то такие интегралы называют собственными.
Если же, хотя бы одно из условий т. Н.-Л. нарушается, то такие интегралы называют несобственными.
Замечание 1. Будем изучать несобственные интегралы 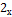 видов:
видов:
1) Несобственный интеграл с бесконечным верхним (нижним) пределом (нарушение условия конечности отрезка  ), а функция на нём непрерывна.
), а функция на нём непрерывна.
2) Собственный интеграл от неограниченной функции (нарушение условия непрерывности 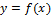 на
на  в какой-то точке, а отрезок конечен).
в какой-то точке, а отрезок конечен).
О.14 (Несобственного интеграла с бесконечным верхним пределом)
Пусть:
1)  непрерывна на
непрерывна на 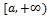 . Несобственным интегралом с бесконечным
. Несобственным интегралом с бесконечным
2) 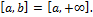 верхним пределом называется:
верхним пределом называется:
 . (1)
. (1)
 – собственные интегралы;
– собственные интегралы;  – числовая последовательность. (2)
– числовая последовательность. (2)
Замечание 2. Отрезок 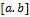 может иметь вид:
может иметь вид:
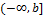 - бесконечный нижний предел;
- бесконечный нижний предел;
 – оба предела интегрирования бесконечны;
– оба предела интегрирования бесконечны;
В случае 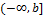 определение даётся аналогично (самостоятельно);
определение даётся аналогично (самостоятельно);
В случае 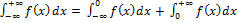 . (3)
. (3)
О.15 (Сходимости интеграла с бесконечным верхним пределом)
Если  конечный предел (1), то
конечный предел (1), то  называют сходящимся;
называют сходящимся;
Если же (1) равен 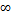 или
или 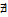 , то
, то  – расходящийся.
– расходящийся.
Теорема 18 (Аналог теоремы Ньютона-Лейбница)
Если на  известна первообразная
известна первообразная 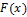 для
для  , то
, то  (4), где
(4), где

Доказательство получится при использовании определения 14,15 и теоремы Ньютона-Лейбница для собственных интегралов  .
.

П.1

П.2

П.3

Замечание 3. Примеры 1, 2, 3 называются эталонными интегралами.
О.16 (сходимости интеграла с бесконечными пределами)
Интеграл (3) называется сходящимся, если сходятся оба интеграла в правой части равенства (3); расходящимся, если расходится хотя бы один из них.
П.4

П.5

| Рис. 11 Геометрический смысл сходящегося несобственного интеграла с бесконечным верхним пределом |
 Геометрический смысл сходящегося несобственного интеграла с бесконечным верхним пределом.
Геометрический смысл сходящегося несобственного интеграла с бесконечным верхним пределом.
Сходящийся несобственный интеграл равен конечной площади бесконечной криволинейной трапеции, т.е.

Где S – заштрихованная площадь.
| Рис. 13 Геометрический смысл сходящегося несобственного интеграла с бесконечными пределами |

| Рис. 12 Геометрический смысл сходящегося несобственного интеграла с бесконечным нижним пределом |
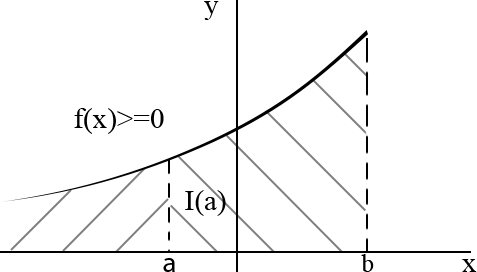
Замечание 4. Если первообразная подынтегральной функции неизвестна, то используют признаки сравнения интегралов (с эталонными).
Теорема 19 (Признак сравнения «допредельный»)
Если для  , т.е. 1) Из сходимости большего интеграла
, т.е. 1) Из сходимости большего интеграла 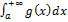 =>
=>
 (5) выполняется сходимость меньшего
(5) выполняется сходимость меньшего  ;
;
 (6) 2) Из расходимости меньшего
(6) 2) Из расходимости меньшего  =>
=>
расходимость большего 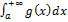 .
.
Доказательство
Очевидно из геометрической иллюстрации на рис. 14
| Рис. 14 Иллюстрация к доказательству теоремы 19. |
 Смотрите и используйте геометрический смысл сходящегося несобственного интеграла с бесконечным верхним пределом!
Смотрите и используйте геометрический смысл сходящегося несобственного интеграла с бесконечным верхним пределом!
Замечание 5. Теорема 19 остаётся справедливой, если неравенство (6) выполняется для 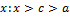 , т.к. (5’)
, т.к. (5’)

| Всегда конечное число |
Первый интеграл в правой части равенства (7) конечное число (как площадь конечной криволинейной трапеции) и поэтому не изменяет факт сходимости (или расходимости) второго интеграла, а только изменяет площадь, если она есть! (см. рис. 15)

| Рис. 15 Иллюстрация к замечанию 5 |
Теорема 20 (Предельный признак сравнения)
Пусть выполняются условия:
1)  и
и  , непрерывны Оба интеграла
, непрерывны Оба интеграла  ,
, 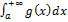
на 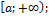 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
2)  (8)
(8)
Доказательство
Из  конечного предела (8) =>
конечного предела (8) =>  удовлетворяющих
удовлетворяющих 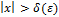 выполняются
выполняются
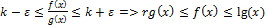 , где
, где  ; далее используем теорему 19.
; далее используем теорему 19.
Замечание 6. При 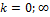 применяется «допредельный» признак.
применяется «допредельный» признак.
| Конечное число |
| Сходится |
| По зам. 4 |

Второй интеграл в правой части равенства сходится по «допредельному» признаку сравнения
| Иллюстрация к примеру 7 |


| Эталонный интеграл |
П.7


О.17 (несобственного интеграла от неограниченной функции)
Пусть
1) 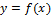 имеет точки Интегралы от таких функций
имеет точки Интегралы от таких функций
разрыва 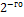 рода либо вида
рода либо вида  называются
называются
на одном из концов  , несобственными интегралами
, несобственными интегралами
либо внутри; от неограниченных функций.
2)  конечен
конечен
Возможны следующие варианты
1)  становится неограниченной 2)
становится неограниченной 2) 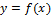 неограниченна 3)
неограниченна 3) 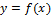 неограниченна
неограниченна
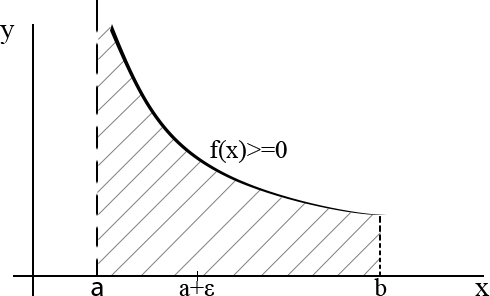
| Рис. 17 1) |
 В правом конце, т.е. при
В правом конце, т.е. при  в левом конце, т.е. при
в левом конце, т.е. при  внутри
внутри  в т.
в т. 
| Рис 17 3) |
| Рис. 17 2) |

О.18 (Сходимости несобственных интегралов от неограниченной функции)
1)

2)

3)
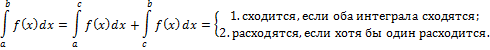
Геометрически: сходящийся  конечной S площади бесконечной криволинейной трапеции.
конечной S площади бесконечной криволинейной трапеции.
Эталонные интегралы:
П.8

П.9, П.10

П.11

Замечание 7. Аналог теоремы Ньютона-Лейбница, оба признака сравнения остаются в силе для интегралов от неограниченных функций. Уметь их формулировать самостоятельно.
Лекция 6 D
| y |
| a |
1. Площадь плоской области
1)
| Рис. 18.1 (Криволинейная трапеция) |
| b |
| x |

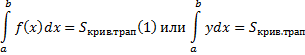
2)
| x |
| y |
| b |
| a |
| D |


Рис. 18.2
(Криволинейная трапеция для f(x)  0) 0)
|
| y |
| D |
| b |
| a |
| x |
3) 
| Рис. 18.3 (Плоская область) |

Замечание 1:
В 1), 2), 3) кривая задана в декартовой системе
координат (д.с.к.)
4) Кривая задана параметрически

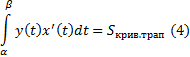
Замечание 2:
Формула (4) получается из (1) заменой y=y(t); dx = x'(t)dt
5) Кривая задана в полярной системе координат:
Теорема 11 (о площади криволинейного сектора):
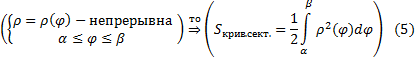

|

|

|
| Рис. 18.4 (Криволинейный сектор) |
Определение 19 (Криволинейного сектора):
Плоская область, ограниченная кривой  , лучами
, лучами  , исходящими из полюса 0, называется криволинейным сектором
, исходящими из полюса 0, называется криволинейным сектором
Доказательство Т.21
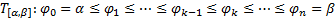

 – сумма площадей круговых секторов
– сумма площадей круговых секторов

2. Объемы тел
Теорема 22 (Вычисление объема тела по известным площадям поперечных сечений):

Доказательство:


 – сумма объемов цилиндров
– сумма объемов цилиндров 

| Рис. 20 (Тело вращения вокруг OX) |
Следствие из Т.22 (об объеме тела вращения):
 При вращении
При вращении  вокруг очи OX вокруг очи OX  (8), что и доказывает равенство (7), если (8) подставить в (6) (8), что и доказывает равенство (7), если (8) подставить в (6)
|
| y |
| x |
| f(x) |
| x |
| Рис. 19 (Иллюстрация у Т.22) |
| b |
| a |

|

|
| x |
Замечание 3:

3. Длина дуги кривой
Пусть дуга È AB задана с помощью вектор-функции
 – непрерывно-дифференцируема
– непрерывно-дифференцируема

 (10)
(10)
Определение 20 (длины дуги кривой):
Длина дуги кривой равна пределу суммы длины вписанной в нее ломаной при  и
и  , т.е.
, т.е. 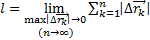 (11)
(11)
Теорема 23: Длина дуги непрерывно-дифференцируемой кривой равна:
 (12)
(12)
Доказательство:
Очевидно вытекает из использования формул (10) и (11):
 , т.к. предел интегральных сумм $ и не зависит от способа разбиения
, т.к. предел интегральных сумм $ и не зависит от способа разбиения  в силу непрерывности производной вектор-функции и, следовательно, модуля от нее.
в силу непрерывности производной вектор-функции и, следовательно, модуля от нее.
| L |

|
| B |
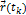
|

|
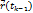
|
| A |
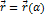
|
| Рис 21. (Иллюстрация к О.20 и Т.23) |
Замечание 4:
Если 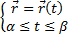 можно расписать параметрически
можно расписать параметрически  , то для
, то для
a) Пространственной кривой –  (13)
(13)
b) Плоской кривой  (14)
(14)
c) При t = x, т.е.  (15)
(15)
d) В полярной системе координат  (16)
(16)
Итак, в 1-й главе: 23 теоремы, 20 определений
Другие приложения рассмотрим на семинарах и самостоятельно.
Глава 2. Интегральное исчисление функции нескольких переменных.
Лекция 7.
Общее определение интеграла по фигуре
Определение 1 (фигуры)
| x 0 a x b |
1)Отрезок [a,b]
Рис. 1 Фигура w-отрезок [a,b]
| Г P (x,y) D |
y
x
Рис.2 Фигура w - плоская область D
3)Пространственное тело V
| P(x,y,z) V |
Y
X Рис.3 Фигура w – пространственная область V
| P (x,y,z) σ |
Рис. 4 w - поверхность σ в пространстве
| B P(x,y,z) A |
Рис.5 w - пространственная кривая L
Определение 2 (Меры фигуры)
Поставим в соответствие "фигуре ω в соответствие положительное число m(ω)>0, которое назовем мерой ω, если:
1) m(ω)=b-a – длина отрезка [a,b];
2) m(ω)=SD – площадь плоской фигуры D;
3) m(ω)=Vтела – объём тела V;
4) m(ω)=Sσ – площадь поверхности σ;
5) m(ω)=l – длина кривой L;
Замечание 1. Мера обладает свойством аддитивности:

Замечание 2. Для удобства записи положим в дальнейшем  .
.
Определение 3 (диаметра ячейки)
Диаметром ячейки  называется наибольшая из хорд этой ячейки
называется наибольшая из хорд этой ячейки
Рис. 6 - Ячейка  и и 
|
| ω |
| PкΔωк |

|
| d(T) |
Рис.7 Иллюстрация определения диаметра разбиения d(T)
Определение 4 (диаметра разбиения)
Пусть Т-разбиение ω на “n” ячеек, пересекающихся по гладким или кусочно-гладким границам.
Диаметром разбиения  называется наибольшая из хорд ячеек:
называется наибольшая из хорд ячеек:

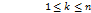
Определение 5 (функции на фигуре)
Если "точке Рϵω  число u=f(p), то говорят, что на ω задана функция u=f(p).
число u=f(p), то говорят, что на ω задана функция u=f(p).
| (1) |
Интегральной суммой Римана называется сумма вида:
 Здесь Δωк –мера ячейки Δωк (см.замечание 2)
Здесь Δωк –мера ячейки Δωк (см.замечание 2)Интегральные суммы(1) зависят от 4-х факторов: ω, f(P), T, Pk
| (2) |

Интегралом Римана по фигуре называется предел интегральных сумм(2) (при  ), если он $ и не зависит от способа разбиения T и выбора точек Pk.
), если он $ и не зависит от способа разбиения T и выбора точек Pk.
Таким образом, интеграл Римана по фигуре зависит от 2-х факторов:
фигуры ω и функции f(P).
Замечание 3. Интеграл по фигуре-это число!
Определение 8 (Интегрируемых функций)
 Теорема1 (без доказательства)
Теорема1 (без доказательства)
 Распишем интеграл по фигуре для каждой конкретной фигуры.
Распишем интеграл по фигуре для каждой конкретной фигуры.
1) ω=[a,b]; dω=dx

| д.с.к. |
| д.с.к. |



| д.с.к. |
| д.с.к. |



4) 


5) 


Геометрический смысл интеграла по фигуре
Пусть

Следовательно,
| д.с.к. |
 2)
2) 

| д.с.к. |

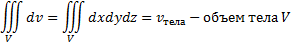
4) 

5) 

Механический смысл интеграла по фигуре

f(P) - переменная плотность массы.
Задание на дом: уметь записывать массу области для всех 5-ти случаев фигур.
Свойство интеграла Римана по фигуре.
Все свойства определенного интеграла по отрезку сохраняются и для остальных фигур:
1)свойство линейности;
2)аддитивности;
4)оценка интеграла;
5)теорема о среднем.
Уметь формулировать все свойства!
Лекция 8
Двойной интеграл в декартовой системе координат.

| д.с.к. |

| д.с.к. |
 (1)
(1)

Поясним (1) и (2).
Т: Для этого разобьем область D на “n” частей прямыми ǁ координатным осям(прямоугольной сеткой)(Рис.7).
Тогда область D разобьётся на n1 внутренних прямоугольных ячеек и m1 -внешних,примыкающих к границе Г, причем n1+m1=n.
Рис.7 - Иллюстрация к формулам (1) и (2)
При  мера внутренних ячеек
мера внутренних ячеек 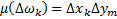 , а мера внешних ячеек
, а мера внешних ячеек  при
при  (т.к. сами ячейки переходят в границу области Г, мера которой в смысле площади = 0).
(т.к. сами ячейки переходят в границу области Г, мера которой в смысле площади = 0).
| д.с.к |
| (2) |

| Z Z=f(x,y)>0 V 0 y=φ(x) y=ψ(x) y a x Dxoy b x |
Цилиндрическим телом V называется фигура, ограниченная сверху поверхностью
 с боков- поверхностью цилиндра, снизу проекцией
с боков- поверхностью цилиндра, снизу проекцией 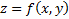 на плоскость XOY, т.е. плоской областью Dxoy .(Рис.8)
на плоскость XOY, т.е. плоской областью Dxoy .(Рис.8)
| Рис.8 Цилиндрическое тело |
Теорема2. (об объеме цилиндрического тела)
Двойной интеграл по проекции Dxoy от f(x,y) равен объему цилиндрического тела V, т.е.

Доказательство.
Разобьем фигуру V разбиением Т плоскостями ǁ координатным плоскостям. Тогда объём фигуры V:

где объём k -ой внутренней ячейки 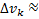 объёму параллелепипеда, а объём l -ой внешней ячейки
объёму параллелепипеда, а объём l -ой внешней ячейки  в смысле меры объёма, т.к. внешние ячейки
в смысле меры объёма, т.к. внешние ячейки  к поверхности.
к поверхности.
Переходя к пределу в (4), получим равенство (3):
