Тема «Определенный интеграл»
1. Если функция y = f (x) непрерывна на отрезке  и F (x) – какая либо ее первообразная на
и F (x) – какая либо ее первообразная на 
 , то формула Ньютона-Лейбница имеет вид:
, то формула Ньютона-Лейбница имеет вид:
А)  ;
;
Б)  ;
;
В)  .
.
2. Если с –постоянное число и функция f (x) интегрируема на  , то
, то
А)  ;
;
Б) 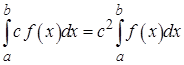 ;
;
В)  .
.
3. Если функция f (x) интегрируема на  и a < c < b, то
и a < c < b, то
А)  ;
;
Б)  ;
;
В)  .
.
4. Если функция f (x) интегрируема на [  ,b ], то f (x) интегрируема и на [ b,
,b ], то f (x) интегрируема и на [ b,  ] и выполняется:
] и выполняется:
А)  =
= 
 ;
;
Б)  =
=  ;
;
В)  =
= 
 .
.
5. Если непрерывные функции удовлетворяют неравенству  ≤
≤  при
при  , то
, то
А)  ;
;
Б)  ;
;
В)  ≤
≤  .
.
6. Если функция f (x) непрерывна на отрезке  , то существует точка
, то существует точка  такая, что:
такая, что:
А)  ;
;
Б) 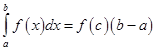 ;
;
В)  .
.
7. Если функция  интегрируема на
интегрируема на  , где
, где  <
<  , а m и M - соответственно наименьшее и наибольшее значения на отрезке
, а m и M - соответственно наименьшее и наибольшее значения на отрезке  , то
, то
А)  ;
;
Б)  ;
;
В)  .
.
8. Площадь фигуры, ограниченной кривыми 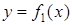 и
и  , прямыми
, прямыми  и
и  (при условии
(при условии  ) определяется по формуле:
) определяется по формуле:
А)  ;
;
Б)  ;
;
В)  .
.
9. Определенный интеграл по частям вычисляется по формуле:
А)  =
=  ;
;
Б)  =
=  ;
;
В)  =
= 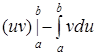 .
.
10. Объем тела, полученного вращением вокруг оси  криволинейной трапеции, ограниченной непрерывной линией
криволинейной трапеции, ограниченной непрерывной линией  , отрезком
, отрезком  и прямыми
и прямыми  и
и  , вычисляется по формуле:
, вычисляется по формуле:
А)  ;
;
Б) 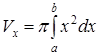 ;
;
В)  .
.
11. Вычислить определенный интеграл  :
:
А) 1
+Б) 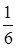
В) 
Г) 6
12. Вычислить определенный интеграл  :
:
+А) 
Б) 
В) 
Г) 
13. Вычислить определенный интеграл  :
:
+А) 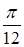
Б) 
В) 
Г) 
14. Вычислить определенный интеграл  :
:
А) 
+Б) 
В) 
Г) 6
15. Вычислить определенный интеграл 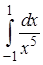 :
:
+А) 
Б) 
В) 
Г) 
Тема «Функции нескольких переменных»
16. Частная производная по х от функции  определяется равенством:
определяется равенством:
А)  ;
;
Б)  ;
;
В)  .
.
17. Частная производная по y от функции  определяется равенством:
определяется равенством:
А) 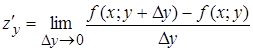 ;
;
Б)  ;
;
В)  .
.
18. Формула для вычисления приближенных значений имеет вид:
А)  ;
;
Б)  ;
;
В)  .
.
19. Точка (х 0 ;у 0) называется точкой максимума функции  , если существует такая
, если существует такая 
 окрестность точки (х 0 ;у 0), что для каждой точки (х, у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
окрестность точки (х 0 ;у 0), что для каждой точки (х, у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
А)  ;
;
Б)  ;
;
В)  .
.
20. Точка (х0;у0) называется точкой минимума функции  , если существует такая
, если существует такая  -окрестность точки (х 0 ;у 0), что для каждой точки (х; у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
-окрестность точки (х 0 ;у 0), что для каждой точки (х; у), отличной от (х0;у0), из этой окрестности выполняется неравенство:
А)  ;
;
Б)  ;
;
В)  .
.
21. Если в точке N (х 0 ;у 0) дифференцируемая функция  имеет экстремум, то ее частные производные в этой точке:
имеет экстремум, то ее частные производные в этой точке:
А) 
 ;
;
Б) 
 ;
;
В) 
 .
.
22. Если  , а
, а  ,
, 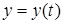 , то
, то
A) 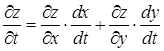 ;
;
Б)  ;
;
В)  .
.
23. Если  , а
, а  ,
,  , то
, то
A)  ;
;
Б)  ;
;
В)  .
.
24. Если  , а
, а  ,
,  , то
, то
A)  ;
;
Б)  ;
;
В)  .
.
25. Частные производные  и
и  неявной функции z, заданной уравнением
неявной функции z, заданной уравнением 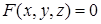 имеют вид:
имеют вид:
А)  ,
,  ;
;
Б)  ,
,  ;
;
В)  ,
,  .
.
26. Уравнение касательной плоскости к поверхности S, заданной уравнением 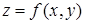 , имеет вид:
, имеет вид:
А)  ;
;
Б) 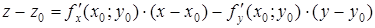 ;
;
В)  .
.
27. Каноническое уравнение нормали к поверхности S, заданной уравнением 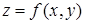 , имеет вид:
, имеет вид:
А)  ;
;
Б)  ;
;
В)  .
.
28. Уравнение касательной плоскости к поверхности S, заданной уравнением 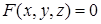 , имеет вид:
, имеет вид:
А)  +
+  ;
;
Б)  +
+  ;
;
В)  +
+  .
.
29. Каноническое уравнение нормали к поверхности S, заданной уравнением 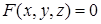 , имеет вид:
, имеет вид:
А)  ;
;
Б)  ;
;
В)  .
.
30. Частная производная функции  по переменной
по переменной 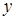 в точке
в точке  равна:
равна:
2 е
31. Частная производная функции  по переменной
по переменной  в точке
в точке  равна:
равна:

32. Частная производная  от функции
от функции  имеет вид:
имеет вид:
А) 
Б) 
В) 
+Г) 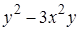
33. Частная производная  от функции
от функции  имеет вид:
имеет вид:
+А) 
Б) 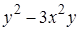
В) 
Г) 
34. Частная производная 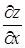 от функции
от функции  имеет вид:
имеет вид:
А) 
+Б) 

В) 
Г) 
35. Частная производная  от функции
от функции  имеет вид:
имеет вид:
+А) 
Б) 

В) 
Г) 
Тема «Числовые и степенные ряды»
36. Числовой ряд  называется сходящимся, если
называется сходящимся, если
А) известна его сумма;
Б) сумма равна любому числу;
В) существует предел конечных сумм;
Г) предел частичных сумм конечный или бесконечный.
37. Если ряд  сходится, то ряд
сходится, то ряд

 :
:
А) расходится;
Б) сходится;
В) сходимость зависит от k;
Г) нельзя сразу ответить на вопрос – требуется исследование.
38. Если числовой ряд  сходится, то:
сходится, то:
А) 
Б) 
В) 
39. Для степенного ряда 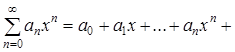 радиус абсолютной сходимости вычисляется по формуле:
радиус абсолютной сходимости вычисляется по формуле:
А) 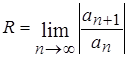
Б) 
В) 
40. Ряд геометрической прогрессии  сходится при:
сходится при:
А) 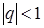
Б) 
В) 
41. Ряд геометрической прогрессии  расходится при:
расходится при:
А) 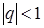
Б) 
В) 
42. Обобщенный гармонический ряд  сходится при:
сходится при:
А) 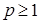
Б) 
В) 
43. Обобщенный гармонический ряд  расходится при:
расходится при:
А) 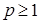
Б) 
В) 
44. Радиус сходимости степенного ряда  равен 9. Тогда интервал сходимости имеет вид
равен 9. Тогда интервал сходимости имеет вид
( )
)
45. Частичная сумма ряда задается равенством  . Тогда сумма ряда равна
. Тогда сумма ряда равна
46. Общий член ряда  имеет вид
имеет вид

47. Первые четыре члена последовательности  имеют вид:
имеют вид:




48. Сумма числового ряда 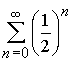 равна…
равна…
А) 2 Б)  В)
В)  Г) 1
Г) 1
49. Ряд  :
:
+А) абсолютно сходится
Б) условно сходится
В) расходится
50. Ряд  :
:
А) абсолютно сходится
+Б) условно сходится
В) расходится