Определите среднее поголовье коров за год.

 

Ниже в таблице сделаем промежуточные расчеты

 

Таблица

Дата	Поголовье коров	Ввод (выбытие) поголовья	Время нахождения введенных (выбывших) коров на ферме, месяцев
на 1 января 1999 г.	300 голов	-
на 1 апреля 1999 г.	330 голов	330-300 = 30	9 (с апреля по декабрь)
на 1 июля 1999 г.	338 голов	338 – 330 = 8	6 (с июля по декабрь)
на 1 октября 1999 г.	320 голов	320-338 = -18	9 (с января по октябрь)
на 1 января 2000 г.	316 голов.	316-320=-4	12 (с января по декабрь)

 

 

где – поголовье скота на начало года;

– поголовье введенное;

– поголовье выбывшее;

Т – время нахождения скота на ферме.

 

 

Ответ: среднее поголовье коров на ферме равно 313.

 

9. Имеются следующие данные о выпуске продукции мебельной фабрики:

 

Наименование изделий	Изменение выпуска в мае по сравнению с апрелем, %	Выпуск продукции в апреле, млн. руб. qo po
Столы	+12
Диваны	+10
Стулья	+15

 

Определите увеличение выпуска всей продукции в мае по сравнению с апрелем (в %), т.е. рассчитайте общий индекс физического объема.

 

Общий индекс физического объема продаж:

 

 

 

Ответ: увеличение выпуска всей продукции в мае по сравнению с апрелем составит 11,9%.

 

1. Задание: Определите по формуле Стерджесса число групп n в группировке и величины интервала h для группировки с равными интервалами.

Задание 1.1

 

Определите по формуле Стерджесса число групп п в группировке и величину интервала h для группировки с равными интервалами, если число единиц в совокупности равно 30, а максимальное и минималь­ное значения признака в совокупности равны соответственно 1100 и 400.

 

Оптимальная величина интервала определяется по формуле:

где х_max, х_min – соответственно максимальное и минимальное значение в выборке;

n – количество наблюдений.

 

Началом интервального ряда принимаем величину:

 

Число групп в группировке	Начало интервала	Конец интервала
	459,25	577,75
	577,75	696,25
	696,25	814,75
	814,75	933,25
	933,25	1051,75
	1051,75	1170,25

Ответ: 6 групп в группировке, величина интервала 118,5.

 

Задание 1.2

 

Определите по формуле Стерджесса число групп п в группировке и величину интервала h для группировки с равными интервалами, если число единиц в совокупности равно 70, а максимальное и минималь­ное значения признака в совокупности равны соответственно 35 и 1.

 

Оптимальная величина интервала определяется по формуле:

где х_max, х_min – соответственно максимальное и минимальное значение в выборке;

n – количество наблюдений.

 

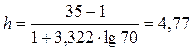
Началом интервального ряда принимаем величину:

 

Число групп в группировке	Начало интервала	Конец интервала
	-1,385	3,385
	3,385	8,155
	8,155	12,925
	12,925	17,695
	17,695	22,465
	22,465	27,235
	27,235	32,005
	32,005	36,775
	36,775	41,545

 

Ответ: 9 групп в группировке, величина интервала 4,77.

 

Задание 1.3

 

Определите по формуле Стерджесса число групп п в группировке и величину интервала h для группировки с равными интервалами, если число единиц в совокупности равно 150, а максимальное и минималь­ное значения признака в совокупности равны соответственно 800 и 20.

Оптимальная величина интервала определяется по формуле:

 

 

где х_max, х_min – соответственно максимальное и минимальное значение в выборке;

n – количество наблюдений.

 

 

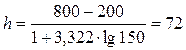
Началом интервального ряда принимаем величину:

 

 

 

Число групп в группировке	Начало интервала	Конец интервала

 

Ответ: 9 групп в группировке, величина интервала 72.

 

Задание 1.4

 

Определите по формуле Стерджесса число групп п в группировке и величину интервала h для группировки с равными интервалами, если число единиц в совокупности равно 250, а максимальное и минималь­ное значения признака в совокупности равны соответственно 2000 и 120.

 

Оптимальная величина интервала определяется по формуле:

где х_max, х_min – соответственно максимальное и минимальное значение в выборке;

n – количество наблюдений.

 

Началом интервального ряда принимаем величину:

 

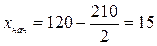
Число групп в группировке	Начало интервала	Конец интервала

 

Ответ: 10 групп в группировке, величина интервала 210.

 

2. Задание: Определите среднее значение по формуле средней арифметической взвешенной.

 

Задание 2.1

 

Имеется следующее распределение 60 рабочих по тарифному раз­ряду:

 

Таблица 2.1

Тарифный разряд, х
Число рабочих, f

 

Нужно определить средний тарифный разряд рабочих.

 

 

где – тарифный разряд в i-ой группе рабочих;

– число рабочих в i-ой группе

 

 

Ответ: средний тарифный разряд рабочих 3,9.

 

Задание 2.2

Определить по данному дискретному вариационному ряду сред­ний курс продажи акции.

 

Таблица 2.2

Курс продажи акции (руб), х
Количество проданных акций (шт), f

 

Средний курс продажи акций равен:

 

 

где – курс продажи акций в i-ой группе;

– число акций в i-ой группе

 

 

Ответ: средний курс акций 1112,9.

 

 

Задание 2.3

Вычислить средний стаж работников рекламного агентства по дан­ным таблицы.

 

Таблица 2.3

Стаж работы (годы), х
Количество работников (чел),f

 

Средний стаж работы равен:

 

 

где – стаж работы работников в i-ой группе;

– количество работников в i-ой группе

 

 

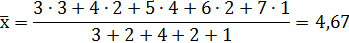
Ответ: средний стаж работников равен 4,67 года.

 

Задание 2.4

 

Определить среднюю долю экспорта предприятий в товарной про­дукции по данным таблицы.

 

Таблица 2.4

Номер предприятия
Доля экспорта в товарной продукции (%), х	0,15	0,2	0,3
Товарная продукция предприятий (млн.руб), f

 

Средняя доля экспорта предприятия в товарной продукции равна:

 

 

 

где – доля экспорта в товарной продукции у i-ого предприятия;

– товарная продукция i-ого предприятия.

 

 

Ответ: Средняя доля экспорта предприятия в товарной продукции равна 0,276.

 

 

3. Задание. Рассчитать дисперсию, среднее квадратическое отклонение и коэффициент вариации для дискретного вариационного ряда.

 

Таблица 3.1

Вычислить дисперсию, среднее квадратическое отклонение и ко­эффициент вариации для дискретного вариационного ряда по данным таблицы 3.1.

 

Таблица 3.1

Произведено продукции одним рабочим за смену, шт., х
Число рабочих, f

 

Решение представить в табличной форме.

Дисперсия:

 

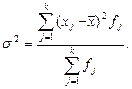
Среднее квадратическое отклонение ,

 

Для оценки интенсивности вариации рассчитывают коэффициент вариации:

 

 

Среднее количество произведенной продукции одним рабочим равно:

 

Проведем расчет в табличной форме.

Итого

 

 

 

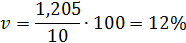
Ответ: среднее квадратическое отклонение равно 1,205 шт; коэффициент вариации составляет 12%.

Задание 3.2

 

По данным таблицы 2.1 из задания 2 определить дисперсию, сред­нее квадратическое отклонение и коэффициент вариации для дискрет­ного вариационного ряда.

 

Таблица 2.1

Тарифный разряд, х
Число рабочих, f

 

Дисперсия:

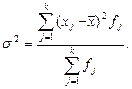
Среднее квадратическое отклонение ,

 

Для оценки интенсивности вариации рассчитывают коэффициент вариации:

 

 

 

Проведем расчет в табличной форме.

		3,61	28,88
		0,81	12,96
		0,01	0,17
		1,21	14,52
		4,41	30,87
Итого			87,4

 

 

Ответ: среднее квадратическое отклонение равно 1,207; коэффициент вариации составляет 30,95%.

 

Задание 3.3

По данным таблицы 2.3 задания 2 определить дис­персию, среднее квадратическое отклонение и коэффициент вариа­ции для дискретного вариационного ряда.

 

Таблица 2.3

Стаж работы (годы), х
Количество работников (чел),f

 

Средний стаж работы равен:

 

 

где – стаж работы работников в i-ой группе;

– количество работников в i-ой группе

 

 

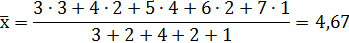
Дисперсия:

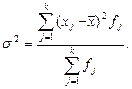
Среднее квадратическое отклонение ,

 

Для оценки интенсивности вариации рассчитывают коэффициент вариации:

 

 

Проведем расчет в табличной форме.

		2,7889	8,366
		0,4489	0,897
		0,1089	0,435
		1,7689	3,537
		5,4289	5,428
Итого			18,67

 

 

Ответ: среднее квадратическое отклонение равно 1,556 лет; коэффициент вариации составляет 33,32%.

 

Задание 3.4

 

По данным таблицы 2.4 задания 2 определить диспер­сию, среднее квадратическое отклонение и коэффициент вариации для дискретного вариационного ряда.

 

Таблица 2.4

Номер предприятия
Доля экспорта в товарной продукции (%), х	0,15	0,2	0,3
Товарная продукция предприятий (млн.руб), f

 

Средняя доля экспорта предприятия в товарной продукции равна:

 

 

 

где – доля экспорта в товарной продукции у i-ого предприятия;

– товарная продукция i-ого предприятия.

 

 

Дисперсия:

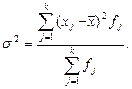
Среднее квадратическое отклонение ,

 

Для оценки интенсивности вариации рассчитывают коэффициент вариации:

 

 

 

Проведем расчет в табличной форме.

0,15		0,013689	2,73
0,2		0,004489	2,065
0,3		0,001089	0,653
Итого			5,456

 

 

 

Ответ: среднее квадратическое отклонение равно 0,066; коэффициент вариации составляет 23,91%.

 

4. Задание. Определите с заданной вероятностью p предельной ошибки выборочной средней и доверительных интервалов при собственно случайном повторном отборе.

 

Задание 4.1.

 

Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате был установлен средний вес дета­ли 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить пределы, в которых находится средний вес деталей в генеральной совокупности.

 

Найдем доверительный интервал, используя формулы:

 

 

где – средний вес детали, г;

–среднеквадратическое отклонение, г;

– количество изделий в выборке;

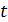– значение, определяемое по таблице Функций Лапласса.

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.954/2)=0.477

t (γ) = (0,477) = 2

 

 

С вероятностью 0,954 можно утверждать, что средний вес изделия не выйдет за пределы 28,21 ÷ 31,78 г.

 

 

Задание 4.2

 

В порядке случайной повторной выборки было обследовано 900 деревьев, по этим данным установлен средний диаметр одного дере­ва 235 мм и среднее квадратическое отклонение, равное 27 мм. С вероятностью 0,683 определите границы, в которых будет находиться средний диаметр деревьев в генеральной совокупности.

Найдем доверительный интервал, используя формулы:

 

 

где – средний диаметр ствола дерева, мм;

–среднеквадратическое отклонение, мм;

– количество деревьев в выборке;

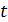– значение, определяемое по таблице Функций Лапласса.

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.683/2)=0.341

 

t (γ) = (0,341) = 1

 

 

С вероятностью 0,683 можно утверждать, что средний диаметр ствола не выйдет за пределы 234,1 ÷ 235,9 мм.

 

 

Задание 4.3

 

Для определения зольности угля месторождения в порядке слу­чайной повторной выборки из партии было взято 100 проб продукта А. В результате исследования установлена средняя влажность продукта А в выборке 9% при среднем квадратическом отклонении 1,5%. С веро­ятностью 0,954 определите пределы, в которых находится средняя влаж­ность продукта А в партии.

Найдем доверительный интервал, используя формулы:

 

 

где – средний влажность пробы, %;

–среднеквадратическое отклонение, %;

– количество проб в выборке;

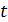– значение, определяемое по таблице Функций Лапласса.

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.954/2)=0.477

 

t (γ) = (0,477) = 2

 

 

С вероятностью 0,954 можно утверждать, что средняя влажность пробы не выйдет за пределы 8,7 ÷ 9,3 %.

 

 

Задание 4.4

Методом собственно-случайной повторной выборки обследована жирность молока у 100 коров. По данным выборки средняя жирность молока оказалась равной 3,64, а среднее квадратическое отклонение составило 1,6%. С вероятностью 0,954 определите пределы, в которых находится средняя жирность молока.

Найдем доверительный интервал, используя формулы:

 

 

где – средняя жирность молока, %;

–среднеквадратическое отклонение, %;

– количество обследованных коров;

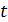– значение, определяемое по таблице Функций Лапласса.

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.954/2)=0.477

 

t (γ) = (0,477) = 2

 

 

С вероятностью 0,954 можно утверждать, что средняя жирность молока не выйдет за пределы 3,32 ÷ 3,96 %.

 

 

5. Задание. Рассчитать необходимую численность выборки по формуле бесповторного отбора для собственно-случайного отбора и механического отбора.

 

Задание 5.1.

В районе А проживает 2000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при, условии, что ошибка выборочной средней не должна превышать 0,8 человека с вероятностью р = 0,954 и при среднем квадратическом от­клонении 2,0 человека.

 

Численность бесповторной выборки определяется по формуле:

 

 

где –среднеквадратическое отклонение;

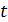– значение, определяемое по таблице Функций Лапласса;

- ошибка выборочной средней;

– численность генеральной совокупности.

 

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.954/2)=0.477

 

t (γ) = (0,477) = 2

 

 

 

Задание 5.2

 

Для определения среднего размера вклада вкладчиков Сбербанка, где число вкладчиков равно 5000, необходимо провести выборку лице­вых счетов методом механического отбора. Предварительно установле­но, что среднее квадратическое отклонение размеров вкладов состав­ляет 120 руб. Определите необходимую численность выборки при усло­вии, что с вероятностью 0,954 ошибка выборки не превысит 10 руб.

Численность бесповторной выборки определяется по формуле:

 

 

где –среднеквадратическое отклонение;

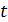– значение, определяемое по таблице Функций Лапласса;

- ошибка выборочной средней;

– численность генеральной совокупности.

 

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.954/2)=0.477

 

t (γ) = (0,477) = 2

 

 

 

Задание 5.3

 

Для установления среднего возраста 50 тыс. читателей библиоте­ки необходимо провести выборку из читательских карточек методом механического отбора. Предварительно установлено, что среднее квад­ратическое отклонение возраста читателей равно 10 годам. Определи­те необходимую численность выборки при условии, что с вероятностью 0,997 ошибка выборки не превысит двух лет.

Численность бесповторной выборки определяется по формуле:

 

 

где –среднеквадратическое отклонение;

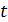– значение, определяемое по таблице Функций Лапласса;

- ошибка выборочной средней;

– численность генеральной совокупности.

 

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.997/2)=0.4985

 

t (γ) = (0,4985) = 2,98

 

 

Задание 5.4

 

На заводе, где работает 10 тыс. рабочих, необходимо установить их средний стаж работы методом механического отбора. Предвари­тельно установлено, что среднее квадратическое отклонение стажа ра­боты равно 5 годам. Определите необходимую численность выборки при условии, что с вероятностью 0,997 ошибка выборки не превысит 1,0 года.

 

Численность бесповторной выборки определяется по формуле:

 

 

где –среднеквадратическое отклонение;

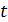– значение, определяемое по таблице Функций Лапласса;

- ошибка выборочной средней;

– численность генеральной совокупности.

 

По таблице функции Лапласа найдем, при каком t значение Ф(t_kp) = (0.997/2)=0.4985

 

t (γ) = (0,4985) = 2,98

 

 

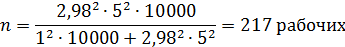
6. Задание. Рассчитать линейный коэффициент корреляции.

 

Задание 6.1.

 

Пусть по 10 однотипным предприятиям имеются следующие дан­ные о выпуске продукции (х) в тыс. ед. и о расходе условного топлива

(у) в тоннах.

 

X
У

 

С помощью линейного коэффициента корреляции определить наличие связи между расходом топлива x и выпуском продукции у.

Результаты представить в табличной форме.

 

Для линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 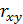, который определяется по формуле:

 

 

Для упрощения расчетов линейного коэффициента корреляции промежуточные расчеты проведены в таблице.

 

Итого

 

Линейный коэффициент корреляции находится в пределах . Чем ближе абсолютное значение к единице, тем сильнее связь между факторами. Полученное значение линейного коэффициента корреляции равно 0,958, значит, есть очень тесная связь между количеством расходом топлива и выпуском продукции.

 

Задание 6.2

 

По следующим данным определить линейный коэффициент кор­реляции между возрастом оборудования (продолжительностью эксплу­атации) и затратами на его ремонт.

 

Возраст оборудования, лет х
Затраты на ремонт, тыс. руб., у	1,5	2,0	1,4	2,3	2,7	4,0	2,3	2,5	6,6	1,7

 

Результаты представить в табличной форме.

 

Для линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 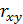, который определяется по формуле:

 

 

Для упрощения расчетов линейного коэффициента корреляции промежуточные расчеты проведены в таблице.

 

		1,5			2,25
		1,4			1,96
		2,3	13,8		5,29
		2,7	21,6		7,29
		2,3	18,4		5,29
		2,5	17,5		6,25
		6,6	72,6		43,56
		1,7	10,2		2,89
Итого			217,1		94,78

 

Линейный коэффициент корреляции находится в пределах . Чем ближе абсолютное значение к единице, тем сильнее связь между факторами. Полученное значение линейного коэффициента корреляции равно 0,886, значит, есть тесная связь между количеством возрастом оборудования и затратами на его ремонт.

 

Задание 6.3

 

По следующим данным определить линейный коэффициент кор­реляции между стажем работы рабочего и выработкой.

 

Стаж работы, лет, х
Выработка за смену, шт. у

 

Для линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 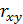, который определяется по формуле:

 

Для упрощения расчетов линейного коэффициента корреляции промежуточные расчеты проведены в таблице.

 

Итого

 

Линейный коэффициент корреляции находится в пределах . Чем ближе абсолютное значение к единице, тем сильнее связь между факторами. Полученное значение линейного коэффициента корреляции равно 0,87, значит, есть тесная связь между стажем работы рабочего и его выработкой.

 

 

Задание 6.4

 

По следующим данным определить линейный коэффициент кор­реляции между выпуском готовой продукции на 1 работающего и электровооруженностью труда.

 

Выпуск готовой продукции, тыс. руб. x	6,3	6,0	7,5	8,5	4,5	6,2	7,5	8,7	6,0	3,7
Элсктровооружснность труда, квт. ч. у

 

Результаты представить в табличной форме.

 

Для линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции 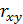, который определяется по формуле:

 

 

Для упрощения расчетов линейного коэффициента корреляции промежуточные расчеты проведены в таблице.

 

	6,3		31,5	39,69
	7,5			56,25
	8,5		59,5	72,25
	4,5		13,5	20,25
	6,2		24,8	38,44

⇐ Предыдущая12

Поделиться: