Билет 30.
Билет 31.
(не нашла точного ответа на этот вопрос, поэтому напечатала только то, что нашла)
Определённый интеграл — аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область во множестве задания этой функции (функционала).
Определение определённого интеграла. Пусть на отрезке [ a, b ] задана функция y = f (x). Разобьём отрезок [ a, b ] произвольным образом на n частей точками [ x 0 , x 1], [ x 1 , x 2], …, [ xi -1, xi ], …, [ xn -1, xn ]; длину i -го отрезка обозначим 
: 
; максимальную из длин отрезков обозначим 
. На каждом из отрезков [ xi -1, xi ] выберем произвольную точку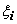 
и составим сумму 
.
Сумма 
называется интегральной суммой. Если существует (конечный) предел последовательности интегральных сумм при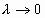 
, не зависящий ни от способа разбиения отрезка [ a, b ]на части [ xi -1, xi ], ни от выбора точек 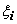, то функция f (x) называется интегрируемой по отрезку [ a, b ], а этот предел называется определённым интегралом от функции f (x) по отрезку [ a, b ] и обозначается 
.
Функция f (x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования.
Кратко определение иногда записывают так: 
.
В этом определении предполагается, что b > a. Для других случаев примем, тоже по определению:
Если b=a, то 
; если b < a, то 
.
Интегральная сумма – сумма,через предел которой вводится определённый интеграл. Интегральные суммы бывают разного вида, наиболее известными являются интегральные суммы Римана и интегральные суммы Лебега. Вместе с интегральными суммами Римана часто используются верхняя 
и нижняя 
суммы Дарбу, где 
Суммы Дарбу – точная верхняя и точная нижняя грани интегральных сумм Римана.
|
|
Если действительная функция f (x) одного переменного x определена на отрезке [ a,b ] и принимает значения из полуотрезка [ A,B), который разбит точками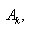 
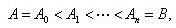и заданы точки 
k= 1,…, n, то интегральной суммой Лебега называется 
где множество 
а 
– мера Лебега множества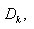 
введённое А. Лебегом обобщение понятия длины. Интеграл Лебега от ограниченных функций определяется через предел таких интегральных сумм и может с помощью них вычисляться приближённо. Для неограниченных функций можно разбивать точками всю ось OY и аналогично вводить бесконечные интегральные суммы Лебега.
Понятие интегральных сумм Лебега можно ввести и для функций нескольких переменных.
Билет 32.
С войства определенного интеграла
1. ∫ badx = b − a
2. Если f интегрируема на [ a, b ], то она интегрируема на любом [ a *, b *], содержащемся в [ a, b ].
3. Пусть a < c < b и функция интегрируема на [ a, c ] и [ c, b ], то ∫ baf (x) dx =∫ caf (x) dx +∫ bcf (x) dx.
4. Если f и g интегрируемы на [ a, b ], то f + g также интегрируема на нем и∫ ba (f (x)+ g (x)) dx =∫ baf (x) dx +∫ bag (x) dx.
5. Пусть функция f интегрируема на [ a, b ], c =const, тогда cf также интегрируема на [ a, b ] и∫ bacf (x) dx = c ∫ baf (x) dx.
6. Если f и g интегрируемы на [ a, b ], то fg также интегрируема на [ a, b ].
7. Если f (x) интегрируема на [ a, b ] и нижняя грань функции ∣ f (x)∣ на [ a, b ] положительна, то и функция 1/ f (x) интегрируема на [ a, b ].
8. Если f (x) неотрицательна и интегрируема на [ a, b ], то ∫ baf (x) dx ≥0.
Следствие. Если f и g интегрируемы на [ a, b ] и для всех x ∈[ a, b ]: f (x)≥ g (x), то ∫ baf (x) dx ≥∫ bag (x) dx
|
|
9. Пусть функция f интегрируема на [ a, b ], тогда: ∫ aaf (x) dx =0, ∫ baf (x) dx =−∫ abf (x) dx, a < b.
10. Пусть функция f интегрируема на [ a, b ], тогда ∣ f (x)∣ также интегрируема на нем и:∣∫ baf (x) dx ∣≤∫ ab ∣ f (x)∣ dx, a < b.
Замечание. Если отказаться от условия a < b, то ∣∫ baf (x) dx ∣≤∣∫ ab ∣ f (x)∣ dx ∣
11. Пусть f (x) -- четная на [− a, a ] и интегрируема на[0, a ], тогда функция f интегрируема на [− a, a ], причем∫ a − af (x) dx =2∫ a 0 f (x) dx.
12. Если нечетная f (x) интегрируема на [− a, a ], то ∫ a − af (x) dx =0.
13. Если f (x) задана при x ≥ a и имеет период T >0 и интегрируема на [ a, a + T ], то каково бы ни было b ≥ a она интегрируема на [ b, b + T ] и имеет место: ∫ b + Tbf (x) dx =∫ a + Taf (x) dx.
ИЛИ
То, что у нас в тетради есть.(свойства интегралов)
Билет 33.
Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x)
и прямыми у=0; х=а; х=b.
Билет 34.
Формула Ньютона — Лейбница.
Сравнивая формулы площади криволинейной трапеции
и 
делаем вывод: если F — первообразная для f на [а; b] то
(1)
Формула (1) называется формулой Ньютона — Лейбница. Она верна для любой функции f, непрерывной на отрезке [а; b]
ИЛИ в тетради(формула Ньютона-Лейбница)Там чуть подробнее, но просто я не могу на компе формулы писать..