Тригонометрические функции

Рассмотрим четыре тригонометрических функции - синус, косинус, тангенс и котангенс, а также графики и основные свойства этих функций.

1. Начнем с построения графика функции y = sin x.

Выберем подходящий масштаб. По оси X: три клетки примем за 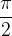(это примерно полтора). Тогда 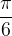- одна клеточка, 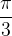- две клетки.
По оси Y: две клетки примем за единицу.

Область определения функции y = sin x - все действительные числа, поскольку значение sin α можно посчитать для любого угла α.

Вспомним, что у нас есть тригонометрический круг, на котором обозначены синусы и косинусы основных углов. Удобнее всего отметить на будущем графике точки, в которых значение синуса является рациональным числом.

x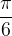
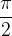
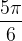
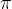
sin x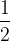

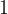
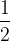
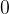
Можем добавить, для большей плавности графика, точк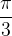и и 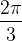. В них значение синуса равно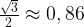
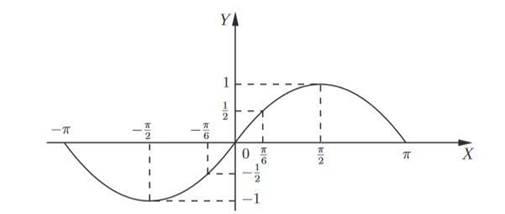
Соединим полученные точки плавной кривой.

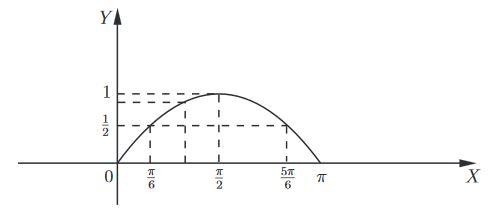
Мы помним, что 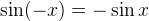. Это значит, что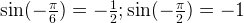
Получается часть графика, симметричная той, которую нарисовали раньше.

Кроме того, значения синуса повторяются через полный круг или через целое число кругов, то есть

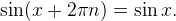
Это значит, что функция y = sin x является периодической. Мы уже построили участок графика длиной 2π. А теперь мы как будто "копируем" этот участок и повторяем его с периодом 2π:

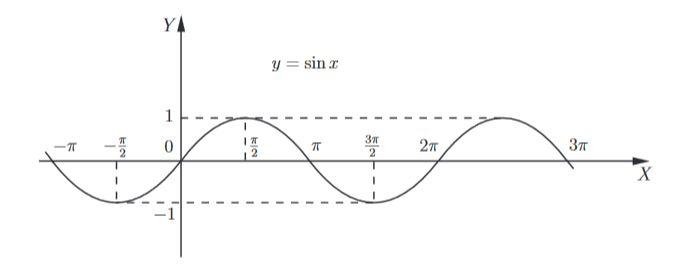
Синусоида построена.
Перечислим основные свойства функции y = sin x.

1) D(y): x ∈ R, то есть область определения - все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = sin x равно единице, а наименьшее - минус единице.

3) Функция y = sin x - нечетная. Ее график симметричен относительно нуля.

4) Функция y = sin x - периодическая. Ее наименьший положительный период равен 2π.

2. Следующий график: y = cos x. Масштаб - тот же. Отметим на графике точки, в которых косинус является рациональным числом:

x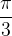
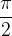
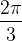
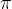
cos x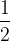

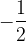
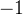
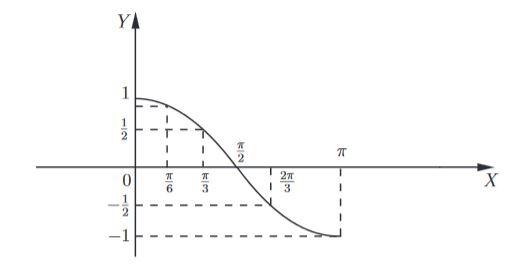
Поскольку cos (−x) = cos x, график будет симметричен относительно оси Y, то есть левая его часть будет зеркальным отражением правой.

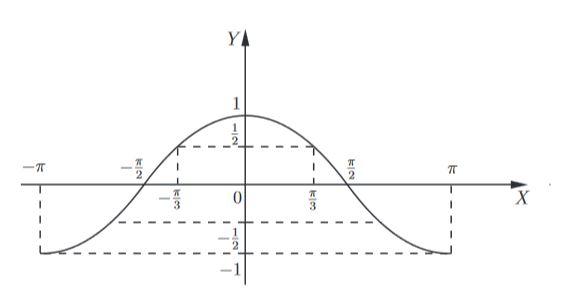
Функция y = cos x - тоже периодическая. Так же, как и для синуса, ее значения повторяются через 2πn. "Копируем" участок графика, который уже построили, и повторяем периодически.

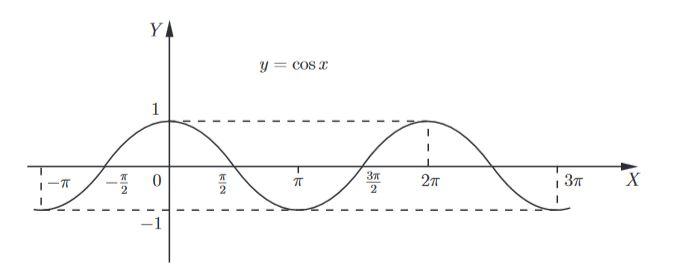
Перечислим основные свойства функции y = cos x.

1) D(y): x ∈ R, то есть область определения - все действительные числа.

2) E(y): y ∈ [−1; 1]. Это означает, что наибольшее значение функции y = cos x равно единице, а наименьшее - минус единице.

3) Функция y = cos x - четная. Ее график симметричен относительно оси Y.

4) Функция y = cos x - периодическая. Ее наименьший положительный период равен 2π.

Отметим еще одно свойство. Графики функций y = sin x и y = cos x весьма похожи друг на друга. Можно даже сказать, что график косинуса получится, если график синуса сдвинуть на 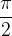влево. Так оно и есть - по одной из формул приведения, .

Форма графиков функций синус и косинус, которые мы построили, очень характерна и хорошо знакома нам. Такой линией дети рисуют волны. Да, это и есть волны!

Функции синус и косинус идеально подходят для описания колебаний и волн - то есть процессов, повторяющихся во времени.

По закону синуса (или косинуса) происходят колебания маятника или груза на пружине. Переменный ток (тот, который в розетке) выражается формулой I(t) = I 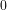cos(ωt+α). Но и это не все. Функции синус и косинус описывают звуковые, инфра– и ультразвуковые волны, а также весь спектр электромагнитных колебаний. Ведь то, что наш глаз воспринимает как свет и цвет, на самом деле представляет собой электромагнитные колебания. Разные длины волн света воспринимается нами как разные цвета. Наши глаза видят лишь небольшую часть спектра электромагнитных волн. Кроме видимого цвета, в нем присутствуют радиоволны, тепловое (инфракрасное) излучение, ультрафиолетовое, рентгеновское и гамма–излучение. Более того - объекты микромира (например, электрон) проявляют волновые свойства.

3. Перейдем к графику функции y = tg x.

Чтобы построить его, воспользуемся таблицей значений тангенса. Масштаб возьмем тот же - три клетки по оси X соответствуют 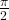, две клетки по Y - единице. График будем строить на отрезке от 0 до π. Поскольку tg (x + πn) = tg x, функ-ция тангенс также является периодической. Мы нарисуем участок длиной π, а затем периодически его повторим.

Непонятно только, как быть с точкой 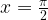. Ведь в этой точке значение тангенса не определено. А как же будет вести себя график функции y = tg x при x, близких к 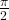, то есть к 90 градусам?

Чтобы ответить на этот вопрос, возьмем значение x, близкое к 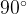, и посчитаем на калькуляторе значения синуса и косинуса этого угла. Пусть .

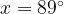Синус угла 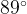- это почти 1. Точнее, sin 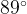= 0,9998. Косинус этого угла близок к нулю. Точнее, cos 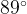= 0,0175.

Тогда график уйдет на 59 единиц (то есть на 118 клеток) вверх. Можно сказать, что если x стремится к 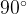(то есть к 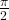, значение функции y = tg x стремится к бесконечности.

Аналогично, при x, близких к 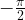, график тангенса уходит вниз, то есть стремится к минус бесконечности.

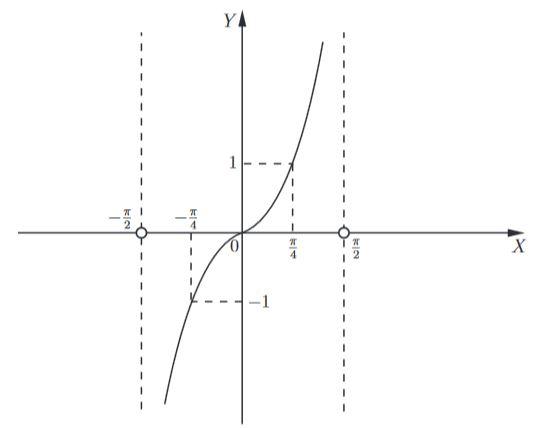
Осталось только "скопировать" этот участок графика и повторить его с периодом π.

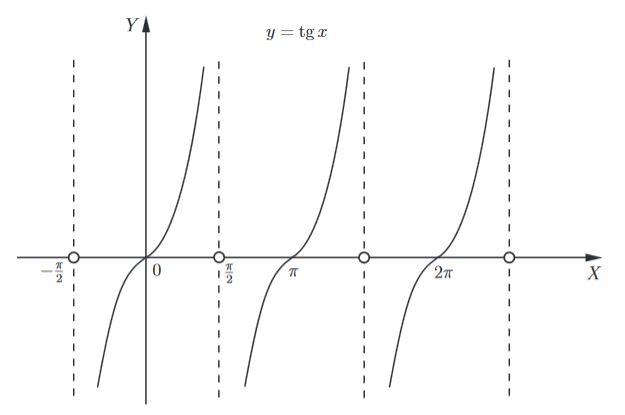
Перечислим свойства функции y = tg x.

1) .
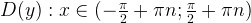Другими словами, тангенс не определен для где n ∈ Z.
2) Область значений E(y) - все действительные числа.

3) Функция y = tg x - нечетная. Ее график симметричен относительно начала координат.

4) Функция y = tg x - периодическая. Ее наименьший положительный период равен π.

5) Функция y = tg x возрастает при 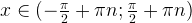то есть на каждом участке, на котором она непрерывна.

4. График функции y = ctg x строится аналогично. Вот он:

1) .
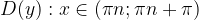Другими словами, котангенс не определен для 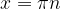где n ∈ Z.
2) Область значений E(y) - все действительные числа.

3) Функция y = сtg x - нечетная. Ее график симметричен относительно начала координат.

4) Функция y = сtg x - периодическая. Ее наименьший положительный период равен π.

5) Функция y = сtg x убывает при 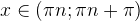то есть на каждом участке, на котором она непрерывна.