2.1. 
2.2. 
2.3. 
2.4. 
2.5. 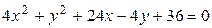
2.6. 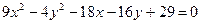
2.7. 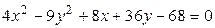
2.8. 
2.9. 
2.10. 
Задание 3. Найти координаты вектора 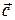 , перпендикулярного векторам
, перпендикулярного векторам  и
и  , если:
, если:
3.1. 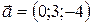 ;
; 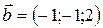 ;
;  .
.
3.2.  ;
;  ;
;  .
.
3.3.  ;
;  ;
;  .
.
3.4. 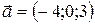 ;
;  ;
;  .
.
3.5. 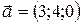 ;
;  ;
; 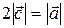 .
.
3.6. 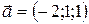 ;
;  ;
; 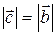 .
.
3.7. 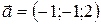 ;
;  ;
;  .
.
3.8. 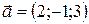 ;
;  ;
;  .
.
3.9.  ;
; 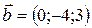 ;
; 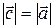 .
.
3.10.  ;
;  ;
;  .
.
Задание 4. Известно, что угол между векторами  и
и  равен
равен  . Найти косинус угла между векторами
. Найти косинус угла между векторами  и
и  , если:
, если:
4.1.  ;
;  ;
;  ;
;  .
.
4.2.  ;
;  ;
; 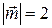 ;
;  .
.
4.3.  ;
; 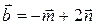 ;
;  ;
; 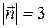 .
.
4.4.  ;
;  ;
; 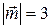 ;
;  .
.
4.5.  ;
; 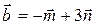 ;
; 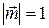 ;
;  .
.
4.6.  ;
;  ;
; 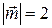 ;
;  .
.
4.7. 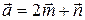 ;
;  ;
; 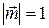 ;
;  .
.
4.8. 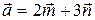 ;
;  ;
; 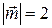 ;
;  .
.
4.9.  ;
;  ;
; 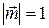 ;
;  .
.
4.10.  ;
; 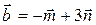 ;
; 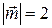 ;
; 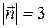 .
.
Задание 5. Даны координаты вершин пирамиды 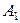


 . Найти: 1) длину ребер
. Найти: 1) длину ребер  ,
,  ,
,  ;
;
2) угол между ребрами 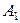
 и
и 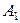
 ;
;
3) площадь грани 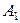

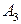 ;
;
4) проекцию вектора 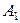
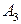 на вектор
на вектор 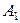
 ;
;
Объем пирамиды.
5.1. 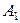 (3, 9, 8);
(3, 9, 8);  (0, 7, 1);
(0, 7, 1); 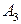 (4, 1, 5);
(4, 1, 5);  (4, 6, 3).
(4, 6, 3).
5.2.  (2, 4, 3);
(2, 4, 3);  (7, 6, 3);
(7, 6, 3); 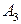 (4, 9, 8);
(4, 9, 8);  (3, 6, 7).
(3, 6, 7).
5.3.  (1, 2, 6);
(1, 2, 6);  (6, 1, 1);
(6, 1, 1); 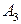 (4, 6, 6);
(4, 6, 6);  (4, 2, 0).
(4, 2, 0).
5.4.  (3, 1, 4);
(3, 1, 4);  (-1, 6, 1);
(-1, 6, 1); 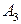 (-1, 1, 6);
(-1, 1, 6);  (0, 4, -1).
(0, 4, -1).
5.5.  (5, 4, 7);
(5, 4, 7);  (2, 4, 7);
(2, 4, 7); 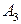 (7, 3, 0);
(7, 3, 0);  (6, 6, 2).
(6, 6, 2).
5.6.  (6, 6, 2);
(6, 6, 2);  (5, 4, 7);
(5, 4, 7); 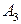 (2, 4, 7);
(2, 4, 7);  (7, 3, 0).
(7, 3, 0).
5.7.  (1, -2, 1);
(1, -2, 1);  (3, 1, -2);
(3, 1, -2); 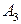 (2, 2, 5);
(2, 2, 5);  (-2, 1, 0).
(-2, 1, 0).
5.8.  (-2, 1, 0);
(-2, 1, 0);  (2, 2, 5);
(2, 2, 5); 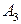 (3, 1, 2);
(3, 1, 2);  (1, -2, 1).
(1, -2, 1).
5.9.  (4, -1, 0);
(4, -1, 0);  (2, 8, 4);
(2, 8, 4); 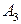 (1, 2, 2);
(1, 2, 2);  (-2, 0, 3).
(-2, 0, 3).
5.10.  (-2, 0, 3);
(-2, 0, 3);  (4, -1, 0);
(4, -1, 0); 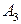 (2, 8, 4);
(2, 8, 4);  (1, 0, 0).
(1, 0, 0).
Задание 6. Дано уравнение прямой l и плоскости  . Найти уравнение плоскости, проходящей через прямую l перпендикулярно плоскости
. Найти уравнение плоскости, проходящей через прямую l перпендикулярно плоскости  .
.
6.1. 
 (l);
(l); 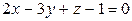 (
( ).
).
6.2. 
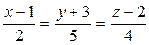 (l);
(l);  (
( ).
).
6.3. 
 (l);
(l); 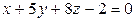 (
( ).
).
6.4. 
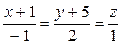 (l);
(l);  (
( ).
).
6.5. 
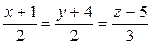 (l);
(l); 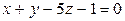 (
( ).
).
6.6. 
 (l);
(l);  (
( ).
).
6.7. 
 (l);
(l);  (
( ).
).
6.8. 
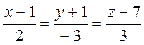 (l);
(l); 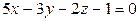 (
( ).
).
6.9. 
 (l);
(l); 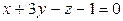 (
( ).
).
6.10. 
 (l);
(l); 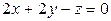 (
( ).
).
Задание 7. Дано общее уравнение прямой 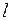 и координаты точки А. Составить:
и координаты точки А. Составить:
а) уравнение плоскости, проходящей через точку А, перпендикулярно прямой 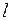 .
.
б) уравнение прямой, проходящей через точку А параллельно прямой 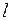 .
.
7.1.  (l); А (1, -1, 2).
(l); А (1, -1, 2).
7.2.  (l); А (3, 0, 2).
(l); А (3, 0, 2).
7.3. 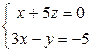 (l); А (5, 2, 3).
(l); А (5, 2, 3).
7.4.  (l); А (-1, -2, 3).
(l); А (-1, -2, 3).
7.5.  (l); А (1, 2, -1).
(l); А (1, 2, -1).
7.6.  (l); А (1, -2, 0).
(l); А (1, -2, 0).
7.7. 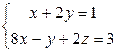 (l); А (2, 1, 0).
(l); А (2, 1, 0).
7.8. 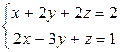 (l); А (1, 2, 0).
(l); А (1, 2, 0).
7.9.  (l); А (1, 2, 3).
(l); А (1, 2, 3).
7.10.  (l); А (-4, 3, 1).
(l); А (-4, 3, 1).
Задание 8. Найти расстояние от точки  до плоскости, проходящей через точки
до плоскости, проходящей через точки  .
.
8.1.  ;
;  ;
; 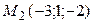 ;
;  .
.
8.2. 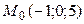 ;
;  ;
; 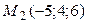 ;
; 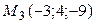 .
.
8.3.  ;
;  ;
;  ;
; 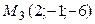 .
.
8.4. 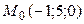 ;
;  ;
;  ;
;  .
.
8.5.  ;
;  ;
;  ;
; 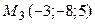 .
.
8.6.  ;
;  ;
; 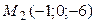 ;
; 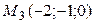 .
.
8.7.  ;
;  ;
;  ;
; 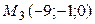 .
.
8.8. 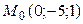 ;
;  ;
;  ;
;  .
.
8.9.  ;
;  ;
; 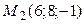 ;
;  .
.
8.10. 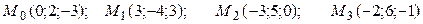 .
.
Задание 9. Найти величину острого угла между прямыми:
9.1. 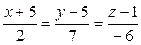 ;
;  .
.
9.2. 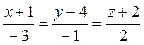 ;
;  .
.
9.3.  ;
;  .
.
9.4.  ;
;  .
.
9.5. 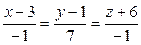 ;
;  .
.
9.6.  ;
;  .
.
9.7.  ;
;  .
.
9.8. 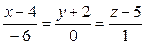 ;
;  .
.
9.9.  ;
; 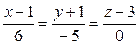 .
.
9.10.  ;
;  .
.
Задание 10. Найти точку пересечения прямой 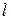 и плоскости
и плоскости 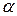 :
:
10.1. 
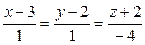 ;
; 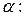
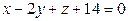 .
.
10.2. 
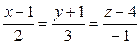 ;
; 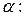
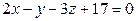 .
.
10.3. 
 ;
; 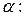
 .
.
10.4. 
 ;
; 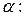
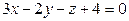 .
.
10.5. 
 ;
; 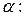
 .
.
10.6. 
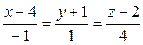 ;
; 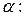
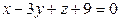 .
.
10.7. 
 ;
; 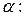
 .
.
10.8. 
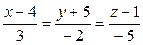 ;
; 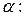
 .
.
10.9. 
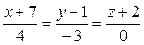 ;
; 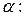
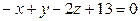 .
.
10.10. 
 ;
; 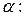
 .
.
Задание 11. Найти точку  , симметричную точке
, симметричную точке 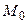 относительно плоскости
относительно плоскости 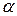 :
:
11.1. 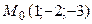 ;
; 
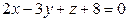 .
.
11.2. 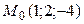 ;
; 
 .
.
11.3.  ;
; 
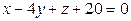 .
.
11.4.  ;
; 
 .
.
11.5.  ;
; 
 .
.
11.6. 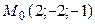 ;
; 
 .
.
11.7. 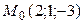 ;
; 
 .
.
11.8.  ;
; 
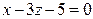 .
.
11.9.  ;
; 
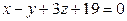 .
.
11.10.  ;
; 
 .
.
Контрольная работа № 3
«Введение в математический анализ»
Задание 1. Найти предел:
1.1. 
1.2. 
1.3. 
1.4. 
1.5. 
1.6. 
1.7. 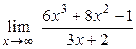
1.8. 
1.9. 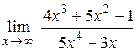
1.10. 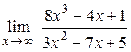
Задание 2. Найти предел:
2.1. 
2.2. 
2.3. 
2.4. 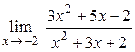
2.5. 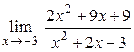
2.6. 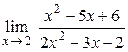
2.7. 
2.8. 
2.9. 
2.10. 
Задание 3. Найти предел:
3.1. 
3.2. 
3.3. 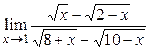
3.4. 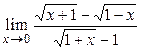
3.5. 
3.6. 
3.7. 
3.8. 
3.9. 
3.10. 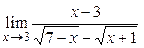
Задание 4. Найти предел:
4.1. 
4.2. 
4.3. 
4.4. 
4.5. 
4.6. 
4.7. 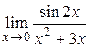
4.8. 
4.9. 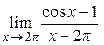
4.10. 
Задание 5. Найти предел:
5.1. 

5.2. 
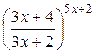
5.3. 

5.4. 

5.5. 
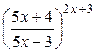
5.6. 

5.7. 

5.8. 

5.9. 
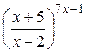
5.10. 

Программа общего курса высшей математики во II семестре.
III. Дифференциальное исчисление функций одной переменной.
1. Производная функции. Основные правила дифференцирования. Таблица производных.
2. Производная сложной и обратной функций. Дифференцирование функций, заданных параметрически и неявно. Логарифмическое дифференцирование.
3. Дифференциал функции. Производные и дифференциалы высших порядков.
4. Теоремы Ферма, Ролля, Лагража, Коши. Правило Лопиталя.
5. Общая схема исследования функции. Построение графиков функций.
IV. Интегральное исчисление.
1. Первообразная и неопределенный интеграл. Основные свойства неопределенных интегралов. Таблица основных интегралов.
2. Основные приемы интегрирования: непосредственное интегрирование, метод подстановки, метод интегрирования по частям.
3. Интегрирование рациональных, иррациональных, тригонометрических функций.
4. Определенный интеграл и его свойства.
5. Формула Ньютона-Лейбница, формула интегрирования по частям, замена переменных в определенным интеграле.
6. Несобственные интегралы.
7. Приложения определенного интеграла.
Темы реферативных письменных работ (II семестр):
Вариант 1
1. Производная функции, ее геометрический и физический смысл.
2. Несобственный интеграл. Основные понятия. Признаки сходимости несобственных интегралов.
Вариант 2
1. Экстремум функции. Наибольшее и наименьшее значения функции.
2. Интегрирование тригонометрических функций.
Вариант 3
1. Теоремы Ролля и Лагранжа, их геометрический смысл.
2. Первообразная, неопределенный интеграл. Основные свойства неопределенных интегралов.
Вариант 4
1. Основные правила дифференцирования. Логарифмическое дифференцирование.
2. Определенный интеграл, его геометрический смысл. Свойства определенного интеграла.
Вариант 5
1. Дифференцирование функций, заданных параметрически и неявно.
2. Способы вычисления определенного интеграла (метод подстановки, метод интегрирования по частям).
Вариант 6
1. Производная сложной и обратной функций.
2. Интегрирование рациональных функций.
Вариант 7
1. Теорема Коши. Правило Лопиталя.
2. Интегрирование иррациональных функций.
Вариант 8
1. Возрастание и убывание функции.
2. Формула Ньютона-Лейбница для вычисления определенного интеграла.
Вариант 9
1. Дифференциал функции и его геометрический смысл. Производные и дифференциалы высших порядков.
2. Геометрические приложения определенного интеграла (вычисление площадей, длин дуг, объемов тел).
Вариант 10
1. Выпуклость и вогнутость графика функции. Точки перегиба.
2. Метод подстановки и метод интегрирования по частям в неопределенном интеграле.
Контрольная работа № 4
«Производная функции»
Задание 1. Найти производные функций:
1.1. а) 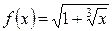 ; б)
; б)  ; в)
; в)  .
.
1.2. а) 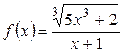 ; б)
; б)  ; в)
; в)  .
.
1.3. а)  ; б)
; б) 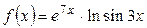 ; в)
; в) 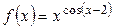 .
.
1.4. а) 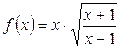 ; б)
; б) 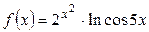 ; в)
; в)  .
.
1.5. а)  ; б)
; б)  ; в)
; в)  .
.
1.6. а) 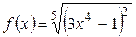 ; б)
; б) 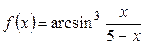 ; в)
; в)  .
.
1.7. а)  ; б)
; б)  ; в)
; в)  .
.
1.8. а)  ; б)
; б) 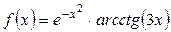 ; в)
; в) 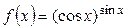 .
.
1.9. а) 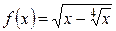 ; б)
; б)  ; в)
; в) 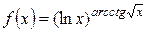 .
.
1.10. а) 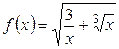 ; б)
; б)  ; в)
; в) 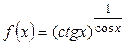 .
.
Задание 2. Найти производные  для неявно заданных функций:
для неявно заданных функций:
2.1.  .
.
2.2. 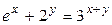 .
.
2.3.  .
.
2.4.  .
.
2.5.  .
.
2.6.  .
.
2.7.  .
.
2.8.  .
.
2.9. 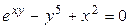 .
.
2.10. 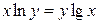 .
.
Задание 3. Найти производные  для функций, заданных в параметрическом виде:
для функций, заданных в параметрическом виде:
3.1.  .
.
3.2.  .
.
3.3. 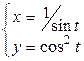 .
.
3.4. 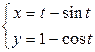 .
.
3.5. 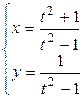 .
.
3.6. 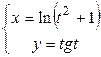 .
.
3.7.  .
.
3.8. 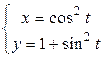 .
.
3.9. 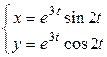 .
.
3.10.  .
.
Задание 4. Найти  и
и  для заданных функций:
для заданных функций:
4.1.  .
.
4.2.  .
.
4.3.  .
.
4.4.  .
.
4.5.  .
.
4.6.  .
.
4.7.  .
.
4.8. 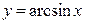 .
.
4.9.  .
.
4.10. 
Контрольная работа № 5
«Исследование функций и построение графиков»