Общие кратные. Наименьшее общее кратное (НОК) чисел а и в.

Пусть А = {1, 2, 3, 4, 8, 12, 24} – множество делителей числа 24.

В = {1, 2,3, 4, 5, 6, 12, 15,б 20, 30,б 60} – множество делителей числа 60.

Очевидно, что всякое натуральное число имеет непустое множество делителей.

Делители числа будем изображать Д_х.

Д_х. = {у | у N₀ х у}. В нашем случае Д₂₄ = {1, 2, 3, 4, 6, 8, 12, 24}, то есть

Д₂₄ = { у | у N 24 у }. Очевидно:

1.( х N)[1 Д_х], то есть 1 является делителем любого натурального числа.

2..( х N)[х Д_х], то есть всякое число является делителем самого себя. Отсюда следует, что х является наибольшим из собственных делителей. Таким образом, множество делителей любого натурального числа является ограниченным подмножеством множества N и, следовательно, – конечным.

3. Наибольший общий делитель чисел а и в не превосходит меньшего из данных чисел, то есть если а < в НОД (а, в) а.

4. Наибольший общий делитель чисел а и в делится на любой общий делитель этих чисел.

Теорема. Любые натуральные числа а и в имеют и при том единственный наибольший общий делитель, то есть ( а, в N₀, в 0)[ 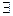! НОД (а, в)].

Доказательство. Число 1 является общим делителем любых двух чисел. Это значит, что множество Д _{(а, в)} – общих делителей чисел а и в не пусто. Из определения общего делителя чисел а и в следует, что ОД (а, в) является пересечением Д _а и Д _в – делителей чисел а и в, и что множество этих делителей конечно. Известно, что конечное подмножество множества N₀ имеет и при том единственный наибольший элемент. Очевидно, что это НОД (а, в).

Общие кратные. Наименьшее общее кратное (НОК) чисел

Определение. Кратным данного натурального числа называется каждое натуральное число, которое делится без остатка на данное число.

Например, числа 4, 8, 12, 16, 20, …, 4n, … являются кратными числу 4.

Обозначают в общем случае К_х.

В нашем случае: К_х = { х | х N₀ х = 4n}. Очевидно, что всякое целое неотрицательное число имеет бесконечное множество кратных ему чисел.

Кроме того ( х N)[0 х] 0 К_х ( х N)[х х] х К_х.

Определение. Общим кратным натуральных чисел а и в называется число кратное каждому из данных чисел. Обозначают: ОК (а, в).

Пусть К_а – множество чисел, кратных числу 6, то есть К_а ={а | а N а = 6n} = {6, 12, 18, 24, 30, 36, …, 6n, …}. К_в – множество чисел, кратных числу 8, то есть К_в = { в | в N в = 8n} = {8, 16, 24,б 32,б 40, 48, …, 8n, …}.

Числа 24, 48, 72, …, 24n есть множество чисел одновременно кратных и числу 6 и числу 8, представляющие собой пересечение множеств К_а и К_в, то есть ОК (а, в) = {24, 48, 72, …, 24n, …}.

Среди чисел кратных одновременно числам 6 и 8, существует такое, которое является наименьшим. В нашем случае это число 24.

Определение. Наименьшее натуральное число из всех общих кратных данных чисел а и в называется наименьшим общим кратным.

Обозначают: НОК (а, в).

В нашем случае НОК (6, 8) = 24.

Так как 0 делится на любое число, то наименьшим общим кратным целых неотрицательных чисел является число 0.

Теорема. Любые натуральные числа а и в имеют, и при том, единственное наименьшее общее кратное, то есть ( а, в N)[ 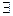! НОК (а, в)].

Доказательство. Произведение а × в а а × в в множество общих кратных чисел а и в не пусто. Известно, что всякое непустое подмножество множества N имеет и при том единственный наименьший элемент. Очевидно, что это НОК (а, в).

Свойства НОК (а, в)

1. Наименьшее общее кратное двух натуральных чисел а и в не меньше большего из данных чисел, то есть если а > в, то НОК (а, в) а.

2. Наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел, то есть если Д (а, в) = 1 К (а, в) = а × в.

3. Любое общее кратное двух натуральных чисел а и в делится на наименьшее общее кратное этих чисел.

Дано: а, в N m = ОК (а, в), m а m в К = НОК (а, в).

Доказать, что m к.

Доказательство. Предположим, что 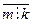, то есть m делится на к с остатком. Тогда по определению деления с остатком m = kq + r, r 0 r = m – kq m а k a (по условию) r a (по теореме о делимости разности).

Аналогично m в k в r = m – kq в, то есть r в.

Таким образом, r a r в.

Если бы r 0, то r = ОК (а, в) и поэтому было бы не меньше К = НОК (а, в), то есть r k, что невозможно, так как остаток меньше делителя.

Следовательно, r = 0. Значит, m = kq m к.

Связь НОК (а, в) и НОД (а, в)

1. Частное от деления произведения чисел а и в на их наименьшее общее кратное есть наибольший общий делитель чисел а и в, то есть , где к = (а, в), d = НОД (а, в).

Доказать, что d = НОД (а, в), то есть а d в d.

Доказательство. Так как k = НОК (а, в) к а к в.

1. Из того, что к а (по свойству монотонности) имеем: вк ак.

Зная, что dk = ав.

Имеем: вк ак dk = ав вк dk в d.

Аналогично, k в ак ав ав = dk ak dk a d.

2. Докажем, что d = НОД (а, в) методом от противного. Предположим, что (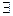 d₁ N)[d₁ = НОД (а, в) d₁ > d]. Тогда по свойству 1: k₁ = = ОК (а, в) но d₁ > d k₁ = < 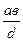= к, к = НОК (а, в). Таким образом, ОК(а, в) = к₁ оказалось меньше их наименьшего общего кратного k, что невозможно. Следовательно, сделанное предположение неверно и d = НОД (а, в).

Следствие. Произведение наибольшего общего делителя и наименьшего общего кратного двух натуральных чисел равно произведению этих чисел, то есть НОД (а, в) × НОК (а, в) = а × в.