Рис. 3. Стек
Очередь – список типа FIFO (First In First Out) – первый пришел, первый ушел (Рис. 4).
Исключить Включить
 | |||||||
 | |||||||
 |  | ||||||



 …
…
Начало Конец
Рис.4. Очередь
 |





 … …
… …
 |  |
Включить/Исключить Включить/Исключить
Рис. 5. Дек
Набор процедур для работы со связанным стеком.
Type ссылка = ^узел;
узел = record
данные: тип;
связь: ссылка
end;
Type стек = ссылка;
Очистка.
Procedure очистить_стек (var s: стек);
Begin
s:= nil
End;
Включение.
Procedure вкл_стек (d: тип данных; var s: стек);
Var x: ссылка;
Begin
new (x);
with x^ do
begin
данные:= d;
связь:= s
end;
s:= x
End;
Исключение.
Function искл_стек (var d: тип данных; var s: стек):boolean;
Var x: ссылка;
Begin
if s = nil then искл_стек:= false
else
begin
искл_стек: = true;
x:= s;
with s^ do
begin
d:= данные;
s:= связь
end;
dispose(x)
end
End;
Переменные в процедурах:
s – указатель на вершину стека;
x – вспомогательная ссылочная переменная;
d – переменная для хранения данных из узла.
Набор процедур для работы со связанной очередью.
Type ссылка = ^узел
узел = record
данные: тип данных;
связь: ссылка
end;
Type очередь = record
l,r: ссылка
end;
Очистка.
Procedure очистить_очередь (var q:очередь);
Begin
q.l = nil;
q.r = nil
End;
Включение.
Procedure вкл_очередь (d: тип данных; var q: очередь);
Var x: ссылка;
Begin
new (x);
if q.l = nil then q.l:= x;
with x^ do
begin
данные:= d;
связь:= nil
end;
q.r^.связь:= x;
q.r:= x
End;
Исключение.
Function искл_очередь (var d: тип данных; var q: очередь): boolean;
Var x: ссылка;
Begin
if q.l = nil then искл_очередь:= false
else
begin
искл_очередь:= true;
x:= q.l;
with x^ do
begin
d:= данные;
q.l:= связь
end;
dispose (x)
end
End;
2. Кольцевые списки. Многосвязные списки, примеры применения.
Циклический список не имеет первого и последнего элементов. Необходимо, следовательно, ввести такие элементы. Удобно использовать внешний указатель, указывающий на последний элемент, что автоматически делает следующий за ним элемент первым (рис.6).
Внешний указатель
lst




 |
Первый элемент Последний элемент
Рис. 6. Циклический список
Можно также ввести соглашение, по которому нулевой указатель представляет пустой циклический список. Циклический список может быть использован для реализации стека или очереди.
Голова (заголовок) циклического списка – специальный узел, который распознаётся по специальному коду, задаваемому в поле данных. Просмотр циклического списка заканчивается по достижению элемента заголовка. Голова помещается в конце или в начале списка.
Указатель циклического списка удобно адресовать к последнему узлу, т.к. в этом случае достаточно просто получить и адрес первого узла, так что циклический список может быть использован как обычная очередь (рис. 7). Необходимо лишь скорректировать процедуры включения и исключения элемента.

 Вход Голова
Вход Голова
 |
Рис.7. Циклический список с заголовком
Пример: Использование двухсвязных двунаправленных списков для представления разреженных матриц.
Разреженная матрица – это матрица высокого порядка, в которой большинство элементов равно нулю. Цель состоит в том, чтобы оперировать с матрицей так, будто матрица представлена в памяти вся, но для экономии не отводить место на нулевые элементы. Рассмотрим такое представление, которое состоит из циклически связанных списков для каждой строки и каждого столбца. Каждый узел матрицы представим в виде записи, содержащей пять полей.
| Влево | Индекс строки | Индекс столбца | Значение | Вверх |
“Влево”, “вверх” - связи со следующим ненулевым элементом слева в строке или сверху в столбце.
 |  |
14 0 0 0
10 0 13 0
- разреженная матрица
0 0 0 0
-15 0 -21 2
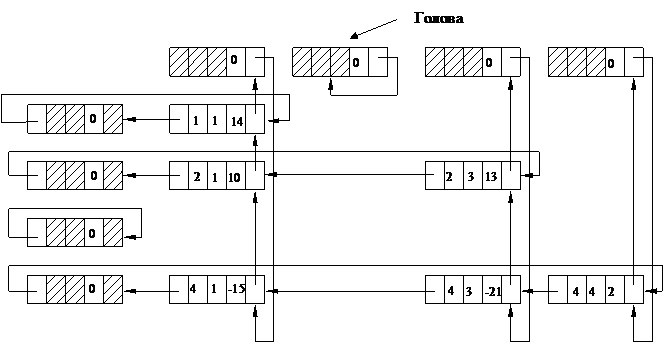
Рис. 11. Представление разреженной матрицы в виде
многосвязного линейного списка
Связь "влево" в головах горизонтальных списков является адресом самого правого значения в строке, а связь “вверх” в головах вертикальных списков является адресом самого нижнего значения в столбце.
При последовательном распределении памяти матрица размера 200*200 заняла бы 40000 слов, в то же время разреженная матрица 200*200 с большим числом нулевых элементов может быть представлена в вышеописанной форме в памяти, содержащей приблизительно 4000 слов (в 10 раз меньше расход памяти).
Разреженные матрицы применяются в алгоритмах решения линейных уравнений, обращения матриц и линейного программирования (симплекс - метод).
3. Древовидная структура, основные понятия. Способы обхода бинарного дерева.
Дерево представляет собой иерархию элементов, называемых узлами. На самом верхнем уровне иерархии имеется только один узел – корень. Каждый узел, кроме корня, связан с одним узлом на более высоком уровне, называемым исходным узлом для данного узла. Каждый элемент может быть связан с одним или несколькими элементами на более низком уровне, которые называются порожденными. Элементы, расположенные в конце ветви, то есть не имеющие порожденных, называются листьями. Дерево обычно изображается в перевернутом виде с корнем вверху, листьями внизу ( рис. 12 ).
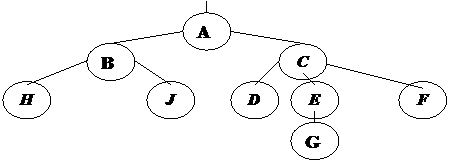
Рис. 12. Древовидная структура
Дерево может быть определено как иерархия узлов с парными связями, в которой:
- самый верхний уровень иерархии имеет один узел, называемый корнем;
- все узлы, кроме корня, связываются с одним и только одним узлом на более высоком уровне по отношению к ним самим.
Степень узла – число непосредственных потомков внутреннего узла.
В примере (рис. 12) степень узлов: A,B – 2, C – 3, E – 1; H,J,D,G,F – 0.
Из-за рекурсивности определения каждый узел дерева можно считать корнем некоторого поддерева. При этом число поддеревьев (порожденных узлов) данного узла называется его степенью.
Если х находится на уровне i, то говорим, что y на уровне i+1. Узел у, который находится непосредственно под узлом х, называется непосредственным потомком х (или сыном, или подчинённым). Узел x называется непосредственным предком y (или исходным, или отцом). Считается, что корень дерева находится на уровне 1 (рис. 13).
 |
i
 |
i+1
Рис. 13. Фрагмент дерева
Уровень узла по отношению к дереву Т определяется следующим образом:
· корень дерева имеет уровень 1;
· корни поддеревьев, непосредственно входящих в дерево, имеют уровни 2,3, и т.д.
Глубина (высота) дерева – максимальный уровень узла дерева (в примере дерево имеет глубину, равную четырем) или число уровней в дереве.
Степень дерева – максимальная степень его узлов (в примере дерево имеет степень = 3, т.к. максимальная степень узла = 3).
Лист (концевой узел, терминальный элемент) – элемент, не имеющий потомков; это узел степени 0 (на рис. 12 H,J,D,G,F – листья).
Внутренний узел (или узел разветвления) – это узел, не являющийся концевым (т.е. не являющийся листом).
Момент – число узлов (в примере – 9).
Вес – число листьев (в примере – 5).
Основание – число корней (в примере – 1).
Длина пути х – число ветвей (ребер), которые необходимо пройти, чтобы продвинуться от корня к узлу х. Корень имеет длину пути 1, его непосредственный потомок – длину пути 2 и т.д. Вообще узел на уровне i имеет длину пути i.
Эти правила рекурсивно определяют представление всякого бинарного дерева в памяти ЭВМ, например, дерево (рис. 16) будет представлено в памяти ЭВМ:
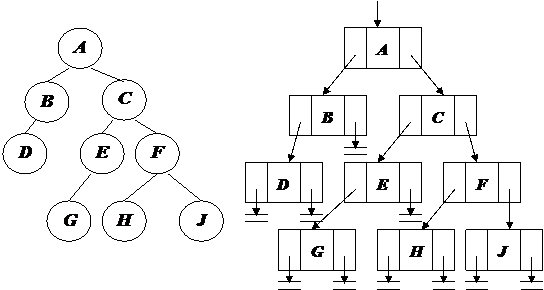 |
Рис. 16. Представление бинарного дерева в памяти ЭВМ
4. Дерево поиска. Включение элементов. Удаление элементов из дерева поиска.
Если дерево организовано таким образом, что для каждого узла Т i все ключи в левом поддереве меньше ключа узла Т i, а ключи в правом поддереве больше ключа узла T i, то это дерево называется деревом поиска.
В дереве поиска можно найти место каждого ключа, двигаясь, начиная от корня, и переходя на левое или правое поддерево каждого узла в зависимости от значения его ключа. N элементов можно организовать в бинарное дерево с высотой h<= log2n, поэтому для поиска среди n элементов может потребоваться не более log2n сравнений, если дерево идеально сбалансировано.
Рассмотрим пример размещения последовательности целых чисел в виде дерева поиска. Будем считать, что в последовательности могут встречаться одинаковые элементы, поэтому в узле будем хранить ключ (само число) и счетчик.
Type ссылка =^ узел;
Узел = record
Ключ: integer;
Счетчик: integer;
Лев, прав: ссылка;
End;
Процесс поиска представим в виде рекурсивной процедуры. Параметр процедуры Р передается как параметр-переменная, а не как параметр-значение. В случае включения переменной должно присваиваться новое значение ссылки, которая перед этим имела значение nil.
Процедура “Поиск по дереву с включением”.
Type ссылка =^ узел;
Узел = record
Ключ: integer;
Счетчик: integer;
Лев, прав: ссылка;
End;
Var i,n,k: integer;
Дерево: ссылка;
Procedure поиск (x:integer; var p: ссылка);
Begin
If p=nil then {узла с ключом х нет в дереве – включить}
Begin
New(p); {создаётся новый узел и p-значение
With p^ do ссылки на него}
Begin ключ:=x; счетчик:=1; лев:=nil; прав:=nil
End
End
Else {продолжать поиск}
With p^ do
Begin if x<ключ then поиск(х,лев)
Else if x>ключ then поиск(х,прав)
Else счетчик:= счетчик + 1;
End
End; {поиск}
Procedure печать_дерева(t:ссылка; h: integer);
{см. процедуру печати дерева}
Begin
Дерево:=nil;
Write(‘число элементов?’); read(n);
For i:=1 to n do
Begin read(k); поиск(к, дерево);
End;
Печать_дерева(дерево,0)
End.
Анализ программы: n=7; числа: 11,5,4,12,5,9,14
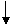 | 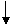 | 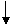 | |||||
 |


 1) 2) 3)
1) 2) 3)
i=1 i=2 i=3


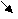

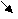

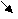 k=11 k=5 k=4
k=11 k=5 k=4

 | 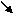 |



 4) 5)
4) 5)




 i=4 i=5
i=4 i=5

 k=12 k=5 6)
k=12 k=5 6)
 i=6
i=6







 k=9
k=9
 |  | ||||||||||||||
 |  | ||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
7)
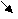 i=7
i=7


 k=14
k=14
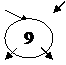 |  | ||||
 | |||||
5. В-деревья, их свойства, построение. Индексирование массивов данных. Индексные деревья.
Рассматриваемые структуры данных называются B – деревьями и имеют следующие свойства:
1. Каждая страница содержит не более 2n элементов (ключей).
2. Каждая страница, кроме корневой, содержит не менее n элементов (n – порядок B – дерева).
3. Каждая страница является либо листом, т.е. не имеет потомков, либо имеет m + 1 потомок, где m – число находящихся на ней ключей.
4. Все листья находятся на одном и том же уровне.
На рис. 21 показано B – дерево порядка 2 с 3-мя уровнями. Все страницы содержат 2, 3 или 4 элемента. Исключением является корень, которому разрешается содержать только один элемент. Все листья находятся на уровне 3.
Ключи расположены в возрастающем порядке слева направо, если спроецировать дерево на один уровень, вставляя потомков между ключами, находящимися на странице – предке.
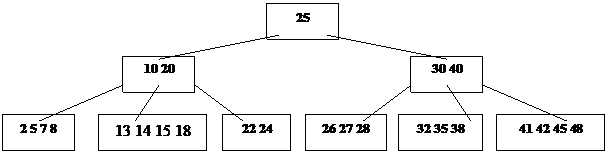 |
Рис. 21. B-дерево порядка 2
Пример: Включение в B–дерево.
Рассмотрим рис. 22

 A
A
|
|
B C
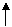 |
Рис. 22. Включение в B–дерево порядка 2
Нужно включить в это дерево элемент с ключом 22.
Включение состоит из этапов:
1. Выяснение, что ключ 22 отсутствует (включение в страницу С невозможно, т.к. она уже заполнена).
2. Страница С расщепляется на две страницы, т.е. размещается новая страница D.
3. Количество m + 1 ключей поровну распределяется на C и D, а средний ключ перемещается на один уровень вверх, на страницу предок А.
На рис. 23 изображено B – дерево (рис. 22) после включения элемента с ключом 22.
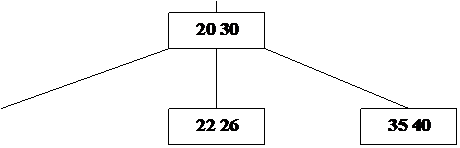 |
A
|
Рис. 23. B – дерево после включения элемента
Пример: Построение B-дерева порядка 2 (n=2) с последовательностью
вставляемых ключей:
20; 40 10 30 15 35 7 26 18 22; 5; 42 13 46 27 8 32; 38 24 45 25;
(точки с запятой указывают моменты размещения новых страниц).
2)
 | 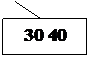 |  | 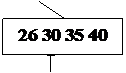 | ||||
|
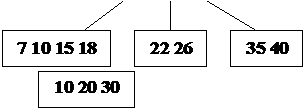 |
4)
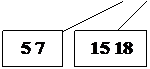 | 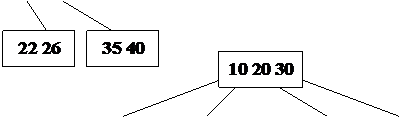 | ||
|
|
|
|
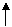 |
|
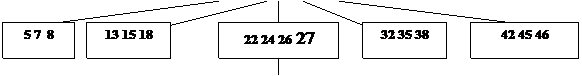
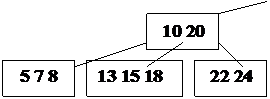 | 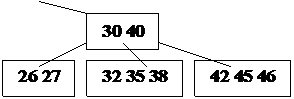 |
Рис. 24. Рост B – дерева порядка 2
6. Применение бинарных деревьев. Кодирование и сжатие данных. Кодовые деревья, дерево Хаффмена.
АЛГОРИТМ ХАФФМЕНА
Рассмотрим следующую проблему. Предположим, что у нас есть алфавит из n символов и длинное сообщение, состоящее из символов этого алфавита. Мы хотим закодировать сообщение в виде длинной строки битов следующим образом (бит определяем как единицу, содержащую 0 или 1). Присвоим каждому символу алфавита определенную последовательность битов (код). Затем соединим отдельные коды символов, составляющих сообщение, и получим кодировку сообщения. Например, предположим, что алфавит состоит из четырех символов — А, В, С и D — и что символам назначены следующие коды:
Символ Код
А 010
B 100
C 000
D 111
Сообщение ABACCDA кодируется как 010100010000000111010. Однако такая кодировка была бы неэффективной, поскольку для каждого символа используются 3 бит, так что для кодировки всего сообщения требуется 21 бит. Предположим, что каждому символу назначен 2-битовый код:
Символ Код
А 00
B 01
C 10
D 11
Тогда кодировка сообщения была бы 00010010101100; требуется лишь 14 бит. Мы хотим найти код, который минимизирует длину закодированного сообщения.
Рассмотрим наш пример еще раз. Каждая из букв B и D появляется в сообщении только один раз, а буква A — три раза. Стало быть, если выбран код, в котором букве A назначена более короткая строка битов, чем буквам B и D, то длина закодированного сообщения будет меньше. Это происходит оттого, что короткий код (представляющий букву А) появляется более часто, чем длинный. В самом деле, коды могут быть назначены следующим образом:
Символ Частота Код
А 3 0
B 1 110
C 2 10
D 1 111
При использовании этого кода сообщение ABACCDA кодируется как 0110010101110, что требует лишь 13 бит. В очень длинных сообщениях, которые содержат символы, встречающиеся чрезвычайно редко, экономия существенна. Обычно коды создаются не на основе частоты вхождения символов в отдельно взятом сообщении, а на основе их частоты во всем множестве сообщений. Для каждого сообщения используется один и тот же код. Например, если сообщения состоят из английских слов, могут использоваться известные данные о частоте появления символов алфавита в английском языке.
Отметьте, что если используются коды переменной длины, то код одного символа не должен совпадать с началом кода другого символа. Такое условие должно выполняться, если раскодирование происходит слева направо. Если бы код символа x—c(x) совпадал с началом кода символа y—c(y), то, когда встречается код c(x), неясно, является ли он кодом символа x или началом кода c (y).
В нашем случае битовая строка сообщения просматривается слева направо. Если первый бит равен 0, то это символ A; в противном случае это B, С или D и проверяется следующий бит. Если второй бит равен 0, то это символ C, иначе это B или D и надо проверить третий бит. Если он равен 0, значит это B, а если 1, то D. Как только распознан первый символ, процесс повторяется для нахождения второго символа, начиная со следующего бита.
Такая операция подсказывает метод реализации оптимальной схемы кодирования, если известны частоты появления каждого символа в сообщении. Находим два символа, появляющихся наименее часто. В нашем примере это B и D. Будем различать их по последнему биту кодов: 0—В, 1—D. Соединим эти символы в единый символ BD, появление которого означает, что это либо символ B, либо символ D. Частота появления этого нового символа равна сумме частот двух составляющих символов. Стало быть, частота BD — 2. Теперь у нас есть три символа: А (частота 3), C (частота 2) и BD (частота 2). Снова выберем два символа с наименьшей частотой, т. е. C и BD. Будем различать их по последнему биту кодов: 0 — С, 1 — BD. Затем два символа объединяются в один символ CBD с частотой 4. К этому времени осталось только два символа — А и CBD. Они объединяются в один символ ACBD. Будем различать их по последнему биту кодов: 0 — А, 1 — CBD.
Символ ACBD содержит весь алфавит, ему присваивается в качестве кода пустая строка битов нулевой длины. Это означает, что вначале раскодирования до момента проверки какого-либо бита известно, что этот символ содержится в ACBD. Двум символам, составляющим ACBD (А и CBD), присваиваются соответственно коды 0 и 1: если встречается 0, значит, закодирован символ A, а если 1, то это C, B или D. Аналогично двум символам, составляющим CBD (С и BD), назначаются соответственно коды 10 и 11. Первый бит указывает, что символ входит в группу CBD, а второй позволяет отличить C и BD. Символам, составляющим BD (В и D), назначаются соответственно коды 110 и 111. Следуя этому процессу, символам, которые появляются в сообщении часто, присваиваются более короткие коды, чем тем, которые встречаются редко.
Операция объединения двух символов в один предполагает использование структуры бинарного дерева. Каждый лист представляет символ исходного алфавита. Каждый узел, не являющийся узлом, представляет соединение символов из листов — потомков данного узла. На рис. 1a приведено бинарное дерево, построенное с использованием предыдущего примера. Каждый узел содержит символ и его частоту. На рис. 1b показано бинарное дерево, построенное по данному методу для приведенной на рис. 1c таблицы символов алфавита и частот. Такие деревья называют деревьями Хаффмена, по имени изобретателя этого метода кодирования.
Как только дерево Хаффмена построено, код любого символа алфавита может быть определен просмотром дерева снизу вверх, начиная с листа, представляющего этот символ. Начальное значение кода — пустая строка. Каждый раз, когда мы поднимаемся по левой ветви, к коду слева приписывается 0; каждый раз при подъеме по правой ветви к коду приписывается 1.
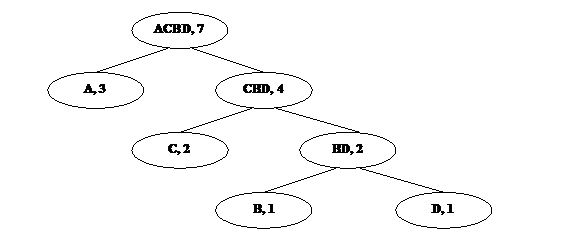
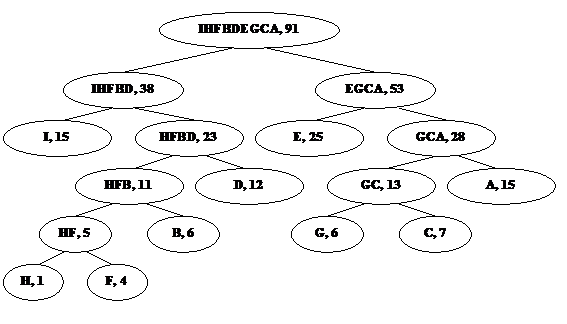 b
b
| Символ Частота Код | Символ Частота Код | Символ Частота Код |
| A 15 111 B 6 0101 C 7 1101 | A 12 011 B 25 10 C 4 01001 | A 6 1100 B 1 01000 C 15 00 |
1c
Рис. 1. Деревья Хаффмена.
Отметьте, что дерево Хаффмена строго бинарное. Следовательно, если в алфавите n символов, то дерево Хаффмена (у которого n листьев) может быть представлено массивом узлов размером 2n-1. Поскольку размер памяти, требуемой под дерево, известен, она может быть выделена заранее. Отметим также, что дерево Хаффмена проходится от листьев к корню. Отсюда следует, что не требуются поля LEFT и RIGHT, и для представления структуры дерева достаточно одного поля FTHER. Знак поля FTHER может использоваться для определения, является ли узел левым или правым сыном, а абсолютное значение поля служит указателем отца узла. Левый сын имеет отрицательное значение поля FTHER, а правый — положительное.
Исходное сообщение (при наличии кодировки сообщения и дерева Хаффмена) может быть восстановлено следующим способом. Начинаем с корня дерева. Каждый раз, когда встречается 0, двигаемся по левой ветви, и каждый раз, когда встречается 1, двигаемся по правой ветви. Повторяем этот процесс до тех пор, пока не дойдем до листа. Новый символ исходного сообщения есть символ, соответствующий этому листу. Проверьте, можете ли вы раскодировать строку 1110100010111011, используя дерево Хаффмена на рис. 1b.
7. Сортировка. Методы вставок и обмена. Метод Шелла. Быстрая сортировка. Обменная поразрядная сортировка.
Метод Шелла
Некоторое улучшение метода сортировки простыми включениями было предложено Д.Шеллом в 1959 году.
Идея метода: Сортируются группы записей, отстоящих друг от друга на заданном расстоянии (например, 8). После сортировки всех таких групп, сортируются группы записей, отстоящих на меньшее расстояние (4) и т.д., пока не дойдём до расстояния, равного 1.
Существует формула для расчёта приращений:
n – количество записей;
t – количество приращений;
t=[log 3 n].
ht=1; hk -1=3*hk+1,
где h – приращение.
Получаем ряд приращений 1,4,13,40,121…
Пример 1. Рассчитать ряд приращений.
n=27; t=3;
h3=1; h2=4; h1=13.
Пример 2. Отсортировать вручную при приращениях 4,2,1.
(4),(2),(1) – приращения
44 55 12 42 94 18 6 67 4 - сортировка
 |





 44 18 6 42 94 55 12 67 2 - сортировка
44 18 6 42 94 55 12 67 2 - сортировка
6 18 12 42 44 55 94 67 1 - сортировка
 |
6 12 18 42 44 55 67 94 результат
Затраты, которые требуются для сортировки n элементов с помощью алгоритма Шелла, пропорциональны n1,2.
Быстрая сортировка (обменная сортировка с разделением).
Это улучшенный метод, основанный на принципе обмена. Неожиданно оказалось, что усовершенствованный «пузырёк» даёт лучший результат из всех известных до настоящего времени методов сортировки. Он обладает столь блестящими характеристиками, что его изобретатель Хоар окрестил его “быстрой сортировкой”, QuickSort (1962г.).
В методе Бэтчера последовательность сравнений предопределена. Она не зависит от фактического состояния файла (т.е. от того, насколько он уже упорядочен). Разумно предположить, что метод сортировки будет эффективнее, если последовательность сравнений элементов зависит от результатов предыдущих сравнений (т.е. будет учитываться состояние файла).
Q-sort основана на том факте, что для достижения наибольшей эффективности желательно производить обмены элементов на больших расстояниях.
Алгоритм:
Массив
i=1 → ← j=N
Пусть имеются два указателя i и j. Причём вначале: i=1, j=N.
Сравним k i и k j (k i: k j). Если обмен не нужен, то уменьшаем j на 1 и повторяем этот процесс.
После первого обмена увеличим i на 1 и будем продолжать сравнения, увеличивая i, пока не произойдёт ещё один обмен, тогда уменьшим j и т.д., пока не станет i=j. К этому моменту запись Ri(Rj) займёт свою окончательную позицию, и исходный файл будет разделён на два подфайла:
(R1,…Ri -1)Ri(Ri+1,…,Rn).
Эти подфайлы надо сортировать независимо (тем же методом).
В процессе сортировки образуется множество подфайлов, которые можно сортировать параллельно, независимо друг от друга.
Если подфайлы будут образовываться последовательно, то информация о неотсортированных подфайлах сбрасывается в стек. При этом целесообразно при образовании двух подфайлов в стек скидывать больший из них. Каждый из подфайлов сортируют методом Q-sort за исключением очень коротких.
Пример:





13 9 18 21 3 4 15 12


 i j
i j

 10 13 9 21 3 4 15 12
10 13 9 21 3 4 15 12
 i i i j
i i i j
 |

 10 13 9 21 3 4 15 18
10 13 9 21 3 4 15 18
 |

 10 13 9 12 3 4 15 18
10 13 9 12 3 4 15 18
 i j
i j

 10 13 9 12 3 4 21 18
10 13 9 12 3 4 21 18
 i j
i j
10 13 9 12 15 3 4 21 18
 i i i =j
i i i =j
1-й файл 2-й файл
 | |||
 | |||

 i j i j
i j i j
 | |||||||||
4 9 12 15 3