Рост с использованием простого и сложного процента
Базовые понятия и определения
Основные зависимости, на которых строятся оценки ценных бумаг, базируются на зависимостях, определяемых как рост по простым и сложным процентам.
Четкое представление о базовых понятиях финансовой математики необходимо для понимания всего последующего материала.
Проценты – это доход от предоставления капитала в долг в различных формах (ссуды, кредиты и т.п.), либо от инвестиций производственного и финансового характера.
Процентная ставка – это величина, характеризующая интенсивность начисления процентов.
Наращивание (рост) первоначальной суммы долга – это увеличение суммы долга за счет присоединения начисленных процентов (дохода).
Множитель (коэффициент) наращения – это величина, показывающая, во сколько раз вырос первоначальный капитал.
Период начисления – это промежуток времени, за который начисляют проценты (получается доход). В дальнейшем будем полагать, что период начисления совпадает со сроком, на который предоставляются деньги.
Интервал начисления – это минимальный период, по прошествии которого происходит начисление процентов.
Существует две концепции и, соответственно, два способа определения и начисления процентов.
Декурсивный способ начисления процентов. Проценты начисляются в конце каждого интервала начисления. Их величина определяется исходя из величины предоставляемого капитала. Соответственно декурсивная процентная ставка, или ссудный процент, представляют выраженное в процентах отношение суммы начисленного за определенный интервал дохода к сумме, имеющейся на начало данного интервала.
Антисипативный способ (предварительный) начисления процентов. Проценты начисляются в начале каждого интервала начисления. Сумма процентных денег определяется исходя из наращенной суммы. Процентной ставкой будет выраженное в процентах отношение, суммы дохода, выплачиваемого за определенный интервал, к величине наращенной суммы, полученной по прошествии этого интервала. Определяемая таким способом процентная ставка называется учетной ставкой или антисипативным процентом.
Простые ставки ссудных процентов
Простые ставки ссудных (декурсивных) процентов применяются обычно в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (как правило, срок менее года), или когда после каждого интервала начисления кредитору выплачиваются проценты.
Введем следующие обозначения:
i (%) - простая годовая ставка ссудного процента;
i - относительная величина годовой ставка процента;
Iг - сумма процентных денег, выплачиваемых за год;
I - общая сумма процентных денег за весь период начисления;
P - величина первоначальной денежной суммы;
S - наращенная сумма;
kн - коэффициент наращения;
n - продолжительность периода начисления в годах;
 - продолжительность периода начисления в днях;
- продолжительность периода начисления в днях;
K - продолжительность года в днях.
Величина K является временной базой для расчета процентов.
Точный процент получают, когда за временную базу беру фактическое число дней в году (365 или 366) и точное число дней ссуды.
Приведенным выше определениям соответствуют формулы:
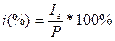 ;(1)
;(1)
 ; (2)
; (2)
 ; (3)
; (3)
S = P + I; (4)
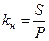 ; (5)
; (5)
 ; (6)
; (6)
 ; (7)
; (7)
 . (8)
. (8)
На практике часто возникает обратная задача: узнать величину суммы P, которая в будущем должна составить заданную величину S (нередко можно встретить синонимы термина «наращенная сумма», «будущая стоимость денег», от англ. Future Value of Money). В этом случае P называют современной (текущей, приведенной, от англ. Present Value of Money) величиной суммы S.
Определение современной величины P наращенной суммы S называется дисконтированием, а определение величины наращенной суммы S – компаундингом.
Из формулы (7) получаем формулу, соответствующую операции дисконтирования:
 . (9)
. (9)
Преобразуя формулу (7) получаем еще несколько формул для определения неизвестных величин в различных случаях:
 ; (10)
; (10)
 ; (11)
; (11)
 . (12)
. (12)
Иногда на разных интервалах начисления применяются разные процентные ставки. Если на последовательных интервалах начисления n1, n2, …, nN используются ставки процентов i1, i2, …, iN, то по формулам (2)и (3) сумма процентных денег в конце первого интервала составит:
I1=Pn1i1,
в конце второго интервала:
I2=Pn2i2
и т.д.
При N интервалах начисления наращенная сумма составит:
 . (13)
. (13)
Для множителя наращения, следовательно, имеем:
 . (14)
. (14)
1.3 Простые учетные ставки
При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (т.е. наращенной суммы). Эта сумма и считается величиной получаемого кредита (или ссуды). Так как в данном случае проценты начисляются в начале каждого интервала начисления, заемщик, естественно, получает эту сумму за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке, а также коммерческим или банковским учетом.
Дисконт – это доход, полученный по учетной ставке, т.е. разница между размером кредита и непосредственно выдаваемой суммой.
Введем следующие обозначения:
d (%) - простая годовая учетная ставка;
d - относительная величина учетной ставки;
Dг - сумма процентных денег, выплачиваемых за год;
D - общая сумма процентных денег;
P - сумма получаемая заемщиком;
S - сумма, которая должна быть возвращена.
Тогда, согласно определениям, получаем следующие формулы:

 ; (15)
; (15)
 ; (16)
; (16)
 ; (17)
; (17)
 ; (18)
; (18)
 . (19)
. (19)
На практике учетные ставки применяются главным образом при учете (покупке) векселей и других денежных обязательств.
Из приведенных формул можно вывести еще две формулы для определения периода начисления и учетной ставки при прочих заданных условиях:
 ; (20)
; (20)
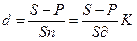 . (21)
. (21)
1.4 Сложные ставки ссудных процентов
Если после очередного интервала начисления доход (т.е. начисленные за данный интервал проценты) не выплачиваются, а присоединяются к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяются формулы сложных процентов. Сложные ссудные проценты в настоящее время являются весьма распространенным видом применяемых в различных финансовых операциях процентных ставок.
Введем следующие обозначения:
ic - относительная величина годовой ставки сложных ссудных процентов;
kн.с. - коэффициент наращения в случае сложных процентов;
j - номинальная ставка сложных ссудных процентов.
Наращенная сумма, по прошествии n лет составит:
 . (22)
. (22)
Множитель наращения kн.с. соответственно будет равен:
 . (23)
. (23)
Если срок ссуды n в годах не является целым числом, множитель наращения определяется по выражению:
 , (24)
, (24)
где, n = na + nb;
na – целое число лет;
nb – оставшаяся дробная часть года.
Предположим, что уровень ставки сложных процентов будет разным на различных интервалах начисления.
Пусть n1, n2, …, nN - продолжительность интервалов начисления в годах; i1, i2, …, iN – годовые ставки процентов, соответствующие данным интервалам. Тогда наращенная сумма в конце первого интервала начисления составит:
 .
.
В конце второго интервала:

и т.д.
При N интервалах начисления наращенная сумма в конце всего периода начисления составит:
 . (25)
. (25)
Начисление сложных процентов может осуществляться не один раз в году. В этом случае оговаривается номинальная ставка процентов j – годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.
При m равных интервалах начисления и номинальной процентной ставке j эта величина считается равной j/ m.
Если срок ссуды составляет n лет, то получаем выражение для определения наращенной суммы:
 , (26)
, (26)
где mn – общее число интервалов начисления за весь срок ссуды.
Если общее число интервалов начисления не является целым числом (mn – целое число интервалов начисления, l – часть интервала начисления), то выражение принимает вид:
 . (27)
. (27)
В мировой практике часто применяется также непрерывное начисление сложных процентов (т.е. продолжительность интервала начисления стремиться к нулю, и m – к бесконечности).
В этом случае для вычисления наращенной суммы служит следующее выражение:
 . (28)
. (28)
Здесь
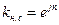 . (29)
. (29)
Аналогично случаю простых процентов полученные формулы можно преобразовывать, выражая одни величины через другие, в зависимости от того, что известно, а что требуется найти.
 . (30)
. (30)
Данная формула, а также соответствующие формулы для случая простых ставок ссудного процента и для учетных ставок дают легко понять, что текущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности.
Также из формулы (22) имеем
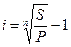 . (31)
. (31)
Из формулы (26):
 . (32)
. (32)
Применяя операцию логарифмирования к обеим частям формулы (22), получаем

 . (33)
. (33)
Подобным же образом из формулы (26) получаем формулу:
 . (34)
. (34)
Существуют несколько правил, позволяющих быстро рассчитать срок удвоения первоначальной суммы для конкретной процентной ставки.
Правило «72»:
 . (35)
. (35)
Правило «69»:
 . (36)
. (36)
1.5 Сложные учетные ставки
Рассмотрим теперь антисипативный способ начисления сложных процентов.
Пусть
dc (%) - сложная годовая учетная ставка;
dc - относительная величина сложной учетной ставки;
kн.у - коэффициент наращения в случае учетной ставки;
f - номинальная годовая учетная ставка.
Тогда по прошествии первого года наращенная сумма S1 составит:
 . (37)
. (37)
По прошествии n лет наращенная сумма составит:
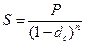 . (38)
. (38)
Отсюда для множителя наращения имеем:
 . (39)
. (39)
Для периода, не являющегося целым числом:
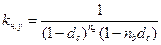 . (40)
. (40)
При учетной ставке, изменяющейся в течение срока ссуды, наращенная сумма превращается в
 . (41)
. (41)
Здесь n1, n2, …, nN - продолжительность интервалов начисления в годах; d1, d2, …, dN – учетные ставки, соответствующие данным интервалам.
Для начисления процентов m раз в году формула имеет вид:
 (42)
(42)
или
 .
.  (43)
(43)
При этом mn – целое число интервалов начисления за весь период начисления, l – часть интервала начисления.
При непрерывном начислении процентов S рассчитывается по формуле:
 . (44)
. (44)
Из полученных формул путем преобразований получаем формулы для нахождения первоначальной суммы, срока начисления и величины учетной ставки:
 ; (45)
; (45)
 ; (46)
; (46)
 ; (47)
; (47)
 ; (48)
; (48)
 . (49)
. (49)
1.6 Эквивалентность процентных ставок различного типа
Эквивалентные процентные ставки – это такие процентные ставки различного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.
Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требует инструмент для конкретного сравнения различных процентных ставок.
Рассмотрим несколько случаев.
Приравнивая соотношения (7) и (19), получим
 ,
,
откуда
 ; (50)
; (50)
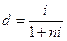 . (51)
. (51)
Из формул (7) и (22), имеем
 ;
;
 ; (52)
; (52)
 . (53)
. (53)
Из формул (7) и (26), имеем
 ;
;
 ; (54)
; (54)
 . (55)
. (55)
Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы (22) и (26):
 ;
;
 ; (56)
; (56)
 . (57)
. (57)
Полученная по формуле (56) годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов.
Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнить процентные ставки в случае, когда используются различные интервалы начисления. Очевидно, что значение эффективной процентной ставки больше значения номинальной, а совпадают они при m = 1.
Далее из формул (22) и (38) имеем
 ;
;
 ; (58)
; (58)
 . (59)
. (59)
Аналогичным образом получаем зависимости между любыми другими эквивалентными процентными ставками.
Проанализировав полученные формулы, можно сделать два замечания:
1. Эквивалентность различных процентных ставок никогда не зависит от величины первоначальной суммы P (для данного рассматриваемого случая, когда первоначальная сумма P предполагается одинаковой).
2. Эквивалентность процентных ставок всегда зависит от продолжительности периода начисления за исключением случая эквивалентности между собой сложных процентных ставок различного вида (если период начисления один и тот же).