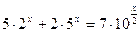Урок 305-306 15.11.2021
Обратная связь: работыприсылать личным сообщением ВК
Задание: проработать конспект, выполнить д/з.
Тема: Решение показательных уравнений
Цель: формировать умения и навыки решать показательные уравнения разными способами и приемами решения показательных уравнений
Какая функция называется показательной? Область определения, область значения показательной функции.
Какое уравнение называется показательным?
Уравнение какого вида называется простейшим показательным уравнением?
Что называется корнем уравнения?
Сформулируйте свойства степени с действительным показателем
Является ли показательным уравнение:
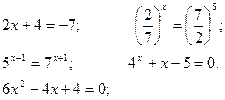
Представьте в виде степени с основанием 2:
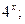
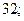
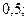
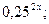
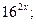
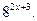
Разложите на множители выражение:
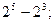
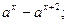
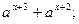
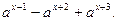
Решите уравнение:
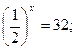
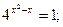
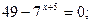
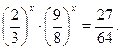
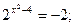
Прокомментируйте приемы упрощения, используемые во время решения уравнения:
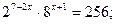
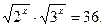
Какие способы и приемы решения вы использовали при анализе?
Притча:
Однажды молодой человек пришел к мудрецу. Каждый день по пять раз я произношу фразу: «Я принимаю радость в мою жизнь», но радости в моей жизни нет. Мудрец положил перед собой ложку, свечу и кружку и попросил «Назови, что ты выбираешь из них». «Ложку», - ответил юноша. «Произнеси это 5 раз». «Я выбираю ложку», послушно произнес юноша 5 раз. «Вот видишь, сказал мудрец, повторяй хоть миллион раз в день, она не станет твоей. Надо… «Что же надо? Надо протянуть руку и взять ложку». Вот и вам надо взять свои знания и применить их на практике.
Сегодня на уроке мы продолжаем работать с показательными уравнениями.
─ Давайте вспомним какие способы мы использовали при их решении?
1) Приведение к одному основанию.
|
|
2) Приведение к общему показателю.
─ Как вы думаете, есть ли другие способы решения показательных уравнений?
─ Значит, что мы будем делать сегодня на уроке?
─ Ожидаемые результаты – научиться решать показательные уравнения разными способами и приемами, приводя их к простейшим.
Усвоение знаний, формирование умений
Рассмотрим разные типы уравнений. Анализируя их решение, мы с вами выведем алгоритм решения каждого типа уравнения.
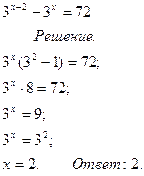
Способ вынесения общего множителя за скобки
1) Вынести общий множитель за скобки
2) Выполнить действие в скобках
3) Разделить левую и правую части на выражение в скобках
4) Решить простейшее показательное уравнение
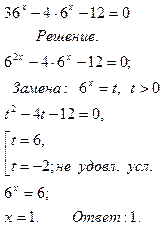
Приведение показательного уравнения к квадратному путем введения новой переменной:
1)Выполняя тождественные преобразования, привести степени к одному основанию
2)Выполнить замену
3)Решить полученное квадратное уравнение
4)Вернуться к замене
5)Решить простейшее показательное уравнение
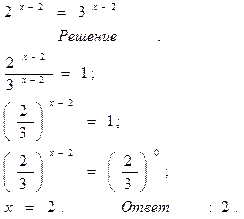
Способ деления левой и правой части уравнения на
одну из степеней:
1) Поделить обе части уравнения на одну из степеней
2) Привести обе части уравнения к одному основанию
3) Решить простейшее показательное уравнение
Решить уравнения
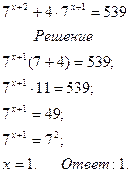
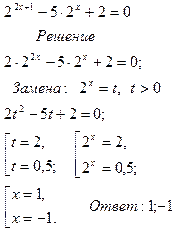
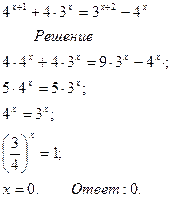
№ 1 № 2
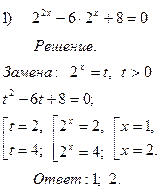
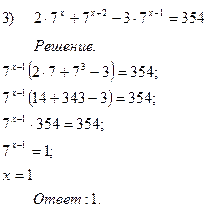
№ 3 № 4
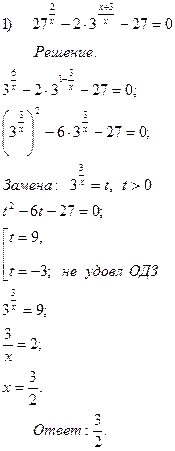
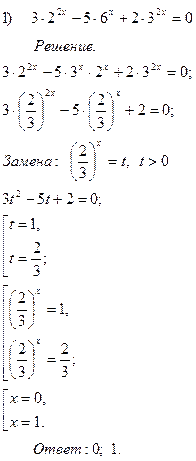
«Метод решения хорош, если с самого начала мы можем предвидеть и впоследствии подтвердить это, что следуя этому методу мы достигнем цели». Лейбниц
Домашнее задание: конспект
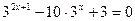 ,
,