Проектирование цифрового фильтра.

Основной недостаток аналоговых активных фильтров, подобных описанному выше, заключается в их малом порядке. Его повышение за счет применения многих звеньев низкого порядка ведет к значительному повышению габаритов фильтров и их стоимости. От этого недостатка свободны современные цифро­вые фильтры, число ячеек которых N даже при однокристальном исполнении может достигать десятков и сотен. Это обеспечивает улучшенную частотную се­лекцию.

Спроектируем фильтр N + 1-го порядка класса FIR (Finite Impulse Response — конечная импульсная характеристика). Зависимость выходного сигнала у от входного х выражается следующим образом:

Загрузим пакет расширения plots, нужный для графической визуализации ре­зультатов проектирования:

Зададим исходные данные для проектирования полосового цифрового фильтра, выделяющего пятую гармонику из входного сигнала в виде зашумленного меан­дра с частотой 500 Гц:

Вычислим некоторые вспомогательные величины и определим функцию Дира­ка (единичного импульса):

Теперь зададим импульсную характеристику полосового фильтра:

Вычислим

FIR-коэффициенты для фильтра с прямоугольным окном:

Определим массивы входного х(п) и выходного у(п) сигналов: Установим х = 0 для времени п * 0 и х = 1 для времени п = 0:

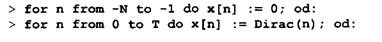
Вычислим временную зависимость для выходного сигнала:

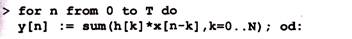
Построим график импульсной характеристики фильтра, отражающей его реак­цию на сигнал в виде одиночного отсчета единичной величины:

Он показан на рис. 4.1. Нетрудно заметить, что эта характеристика свидетель­ствует об узкополосности фильтра, поскольку его частоты среза f 1 и fh разли­чаются не сильно. В этом случае полосовой фильтр по своим свойствам прибли­жается к резонансному (колебательному) контуру, хотя само по себе явление резонанса не используется. Оно лишь моделируется.

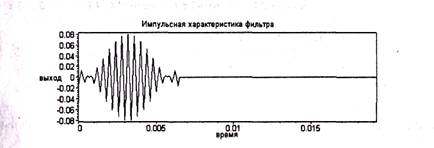
Рис. 4.1. Импульсная характеристика цифрового фильтра

Вычислим АЧХ фильтра, используя прямое преобразование Фурье. Оно, после подготовки

обрабатываемых массивов, реализуется функцией FFT:

Построим график АЧХ фильтра:

Он представлен на рис. 4.2. Нетрудно заметить, что АЧХ фильтра и впрямь напоминает АЧХ резонансной цепи — она имеет вид узкого пика. Однако спады АЧХ выражены явно более резко, чем у резонансного ZCR-контура; кроме того, график имеет характерные боковые лепестки. Вы можете легко проверить, что при большем разносе частот f 1 и fh можно получить АЧХ с довольно плоской вершиной и резкими спадами (говорят, что такая характеристика приближается к прямоугольной).

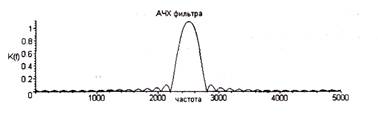
Рис. 4.2. АЧХ цифрового полосового фильтра

Теперь приступим к тестированию созданного фильтра. Зададим входной сиг­нал в виде зашумленного меандра с частотой 500 Гц и полным размахом напря­жения 2 В:

Временная зависимость синтезированного входного сигнала представлена на рис. 4.3.

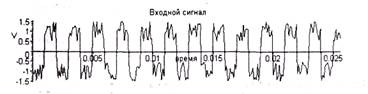
Рис. 4.3.Синтезированный входной сигнал Вычислим реакцию фильтра на входной сигнал:

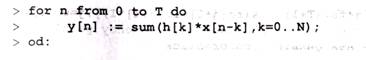
Построим график временной зависимости выходного сигнала:

Эта зависимость показана на рис. 4.4. Нетрудно заметить, что в конце концов выходной сигнал вырождается в пятую гармонику входного сигнала, но этому предшествует довольно длительный переходной процесс. Он связан с узкополосностью данного фильтра.

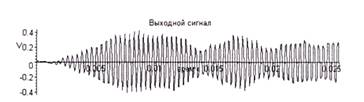
Рис. 4.4. Временная зависимость выходного сигнала цифрового фильтра

Вычислим спектры входного и выходного сигналов, подготовив массивы выбо­рок сигналов и применив прямое преобразование Фурье с помощью функции FFT:

Построим график спектра входного сигнала, ограничив масштаб по амплитуде значением 0,5 В:

Этот график представлен на рис. 4.5. Из него хорошо видно, что спектраль­ный состав входного сигнала представлен только нечетными гармониками, ам­плитуда которых убывает (хотя и не монотонно) по мере роста номера гармоники. Пятая гармоника на частоте 2500 Гц находится посередине полосы пропускания фильтра, ограниченной граничными частотами 2300 и 2700 Гц. Заметны также беспорядочные спектральные линии шумовой составляющей сигнала.

Рис. 4.5. Спектрограмма входного сигнала

 

 

Теперь построим график спектра выходного сигнала:

Он представлен на рис. 4.6. Хорошо видно эффективное выделение пятой гар­моники сигнала и прилегающей к ней узкой полосы шумового спектра.

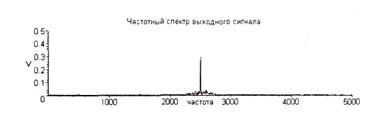
Рис. 4.6. Частотный спектр выходного сигнала.

 

Задание на работу.

- изучить теоретическую часть;

- смоделировать заданную преподавателем функцию и получить ее график.

 

 

Содержание отчета.

Разработанная программа и ее результаты