Вычислить точки перегиба

Исследование функции с помощью производных. Построение графиков функции.

Для чего нужно это исследование? Производная используется для исследования функций, т.е. для её изучения различных свойств. Результаты такого исследования удобно представлять в виде графика. Начнем, конечно же, с плана. Исследование функции - объемная задача,поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

1. Найти область определения. Выделить особые точки (точки разрыва).

2. Найти точки пересечения с осями координат.

3. Установить, является ли функция чётной или нечётной, периодической или нет (только для тригонометрических функций).

4. Найти интервалы монотонности.

5. Вычислить точки экстремума

6. Найти интервалы выпуклости-вогнутости.

7. Вычислить точки перегиба

8. Выбрать дополнительные точки и вычислить их координаты.

9. Построить график функции

Пример1. Исследовать функцию и по результатам исследования построить график.

Решение:
1) Функция определена и непрерывна на всей числовой прямой: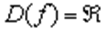

2) Ось OX:. Y= 0 (Нули функции, решить затруднительно)

Ось OY: X= 0 y =3/2

3). Проверим функцию на чётность/нечётность:
:
, значит, данная функция не является чётной или нечётной.

Очевидно, что функция непериодическая.

.
4) Найти интервалы монотонности. (Возрастание, убывание функции.)

· Если функция y = f(x), x 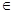(a; b), имеет положительную производную в каждой точке интервала (a; b), то эта функция возрастает на интервале (а; b).

· Если функция y = f(x), x 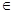(a; b), имеет отрицательную производную в каждой точке интервала (a; b), то эта функция убывает на интервале (a; b).

Правило нахождения интервалов монотонности:

1. Найти производную F¢(x) заданной функции и стационарные точки;

2. Определить интервалы монотонности функции y = F(x);

3. Исследовать знак производной F¢(x) на каждом из найденных интервалов, причем если на каком-либо интервале F¢(x) > 0, то на этом интервале функция y = F (x) возрастает. Если на каком-либо интервале F¢(x) < 0, то на этом интервале функция

y = F(x) убывает.

Найдём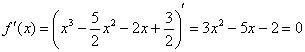

Данное уравнение имеет два действительных корня .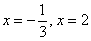

Отложим их на числовой прямой и определим знаки производной:

Следовательно, функция возрастает на 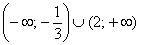и убывает на .

 

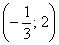4. Вычислим точки экстремума

В точке 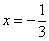функция достигает максимума: .
В точке 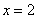функция достигает минимума: .

Выпуклость, вогнутость.

Нахождение интервалов выпуклости и точек перегиба.

Если на интервале (a; b) дважды дифференцируемая функция y = f(x) имеет отрицательную (положительную) вторую производную, то график функции обращен выпуклостью вверх (вниз).

Необходимое условие существования точки перегиба: если функция y = f(x) имеет непрерывные производные до второго порядка включительно на интервале (a;b) и точка (x₀; f(x₀)), где x₀ 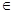(a; b) является точкой перегиба графика функции f(x), то f”(x₀) = 0.

Найдём критические точки второй производной:

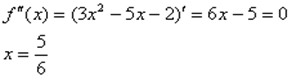
Определим знаки :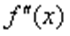

График функции является выпуклым на и вогнутым на .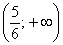

Вычислить точки перегиба

Вычислим ординату точки перегиба: .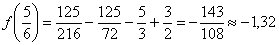

6) Осталось найти дополнительные точки, которые помогут точнее построить график и выполнить самопроверку.:

Выполним чертёж:

Зелёным цветом отмечена точка перегиба, крестиками – дополнительные точки. График кубической функции симметричен относительно своей точки перегиба, которая всегда расположена строго посередине между максимумом и минимумом.

Асимптоты графика функции:

Прямая линия называется асимптотой графика функции f(x), если расстояние от точки М, лежащей на графике, до этой прямой стремится к нулю при движении точки по графику в бесконечность.

Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.

Прямая x = x₀ называется вертикальной асимптотой графика функции f(x), если хотя бы одно из предельных значени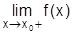й или 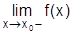равно 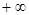или .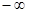

Прямая y = A называется горизонтальной асимптотой графика функции f(x)

при 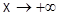(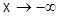), если ().

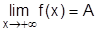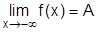Прямая y = kx + b (k ≠ 0) называется наклонной асимптотой графика функции

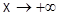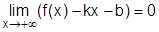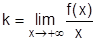y = f(x) при , если , где ; b = .

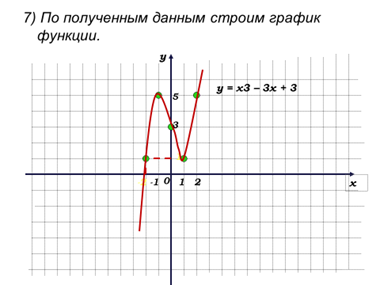
Пример. Постройте график функции у = х³ – 3х + 3, используя краткую схему построения. схему построения.

Решение:

1) D(y) = (-∞; +∞)

2) Найти точки пересечения с осями координат

Y = 0, решить затруднительно

X = 0, Y = 3

3) Функция не является ни четной, ни нечетной, т. к.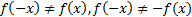

4) f’(x) = 3x² – 3, f’(x) = 0 при х = 1, х = -1.

х = 1, х = -1 – стационарные точки.

5) f’(x)>0 при . Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки возрастания.

f’(x)<0 при 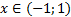. Так как в точках х = 1, х = -1 функция непрерывна, то эти точки также включаются в промежутки убывания.

6) Так как в точке х = -1 производная меняет знак с «+» на «-», то х = -1 – точка максимума.

Так как в точке х = 1 производная меняет знак с «-» на «+», то х = 1 – точка минимума.

7) Результаты исследования представим в виде таблицы.

x	(-∞; -1)	-1	(-1; 1)		(1; +∞)
f’(x)	+		-		+
f(x)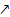
		max		min

8) Координаты некоторых точек (дополнительных):

x	-2
f(x)

9) По полученным данным строим график

 

Для самостоятельного решения:

Пример. Исследовать функцию и построить график.

Вопросы для самоконтроля:

1. Дать определение точек экстремума функции.

2. Как исследовать функцию на монотонность и экстремумы с помощью первой производной?

3. Как находятся интервалы выпуклости кривой и точки перегиба?

 

 

Домашнее задание. Выполнить исследование и построить график функции:

1. y = .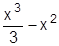

2. y = x³ – x² – x + 3.

3.: y = 6x⁴ – 4x⁶.