Глава 14. Показательные неравенства.
А.
№У14.1) Решите неравенство 
.
№С14.2) Решите неравенство 
.
Ответы к главе 14. №14.1) 
; №14.2) 
.
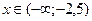В.
№У14. 3) Укажите наименьшее целое решение неравенства 
.
№С14.4) Найдите сумму целых решений неравенства 
.
№У14.5) Найдите сумму целых решений неравенства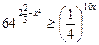 
.
№С14.5.1) Решите неравенство: 
.
№У14.5.2) Решите неравенство: 
.
№У14.6) Найдите сумму целых решений неравенства 
, принадлежащих промежутку 
.
№С14.7) Найдите сумму целых решений неравенства 
, принадлежащих промежутку 
.
Ответы к главе 14. №14.3) -1; №14.4) -6; №14.5) 10; №14.5.1) 
; №14.5.2)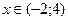 
; №14.6) 3; №14.7) -5.
Глава 15. Упрощение логарифмических выражений.
А.
№У15.1) 
. №У15.2) 
. №С15.3)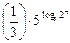 
. №15.4) 
. №15.5) 
. №15.6)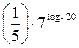 
. №15.7) 
. №15.8) 
.
№15.9)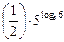 
. №15.10) 
.
№У15.11) Вычислите 
№С15.12) Вычислите 
№У15.13) Найдите значение выражения 
.
№У15.14) Упростить выражение: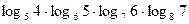 
.
№У15.15) Вычислите 
.
№С15.15.1) Вычислите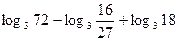 
.
Ответы к главе 15. №15.1) 5; №15.2)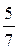 
; №15.3) 9; №15.4) 3,5; №15.5) 5; №15.6) 4; №15.7) 
; №15.8) 1,5; №15.9) 3; №15.10) 
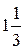; №15.11) 36; №15.12) 4; №15.13) 2; №15.14) 
; №15.15) 2; №15.15.1) 7.
В.
№У15.16) Найдите значение выражения 
.
№С15.17) Найдите значение выражения 
.
№У15.17.1) Вычислите: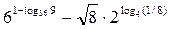 
.
№С15.18) Найти значение выражения 
.
№У15.19) Вычислите 
.
№У15.20) Вычислить: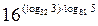 
.
№С15.21) Вычислить: 
.
№У15.22) Найти значение выражения 
№У15.23) Вычислите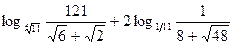 
.
Ответы к главе 15. №15.16) 80; №15.17) 112; №15.17.1) 1; №15.18) 13; №15.19) 1; №15.20)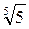 
; №15.21) 1,5; №15.22) -2; №15.23) 8.
Глава 16. Логарифмические уравнения.
А.
№С16.1) Решите уравнение 
.
№У16.2) Решить уравнение 
.
№У16.3) Найдите произведение корней или корень, если он единственный, уравнения 
.
№У16.4) Решите уравнение 
.
№С16.4.1) Решите уравнение 
.
Ответы к главе 16.
№16.1) 0,5; №16.2) -20; №16.3) -25; №16.4) 2; №16.4.1) 
.
В.
№С16.5) Решить уравнение: 
.
№У16.6) Решить уравнение: 
.
№У16.7) Найдите все решения уравнения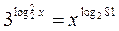 
№С16.7.1) Найдите все решения уравнения 
.
№У16.8) Решите графически уравнение 
. Укажите единичный промежуток (между целыми числами), в котором находится его корень.
Ответы к главе 16. №16.5) -1; №16.6) 3; №16.7) 1; 16; №16.7.1) 1; 81; №16.8) (1;2).
Глава 31. Четырехугольники (трапеция, параллелограмм, ромб).
А.
№У31.1) ABCD – параллелограмм. Найдите его периметр, если периметр треугольника BCD равен 48см и BD=19см.
№С31.2) Найдите площадь фигуры, вершины которой находятся в точках с координатами (-1;0), (0;2), (1;2), (3;0).
№С31.3) Найти площадь трапеции ABCD, если A(1;1), В(5;3), С(5;9), D(1;9).
№С31.4) Найдите площадь четырехугольника ABCD с вершинами в точках 
.
Ответы к главе 31. №31.1) 58 см; №31.2) 5; №31.3) 28; №31.4) 10.
В.
№У31.5) Если 
- внутренние углы выпуклого четырехугольника ABCD и угол C тупой, 
, 
, 
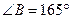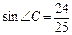, то 
равно…
№У31.6) Найти диагонали ромба, если они относятся как 3:4, а периметр равен 100.
№У31.7) Боковые стороны трапеции продолжены до их взаимного пересечения. Найдите площадь трапеции, если длины ее оснований относятся как 7:5 и площадь всего образовавшегося треугольника равна 49.
№С31.8) Боковые стороны трапеции продолжены до их взаимного пересечения. Найдите площадь трапеции, если длины ее оснований относятся как 5:2 и площадь всего образовавшегося треугольника равна 100.
№У31.9) Две высоты параллелограмма, проведенные из вершины тупого угла к его сторонам равны 4см, 7см, угол между ними равен 
. Найдите площадь параллелограмма.
№С31.9.1) Две высоты параллелограмма, проведенные из вершины тупого угла к его сторонам равны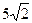 
см, 8см, угол между ними равен 
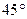. Найдите площадь параллелограмма.
№У31.10) Диагонали равнобедренной трапеции перпендикулярны. Найдите высоту трапеции, если ее площадь равна 25.
Ответы к главе 31. №31.5)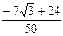 
; №31.6) 30 и 40; №31.7) 24; №31.8) 84; №31.9) 56; №31.9.1) 80; №35.10) 5.
С.
№У31.11) У трапеции ABCD основание AD в 4 раза больше основания BC, а площадь трапеции равна 50. Точка O – точка пересечения диагоналей, точка P – середина основания AD, точка M – точка пересечения диагонали AC и отрезка BP, точка N – точка пересечения диагонали BD и отрезка CP. Найти площадь треугольника MON.
№У31.12) В трапеции ABCD основания BC=2 см, AD=9 см. Точки K и L лежат на боковых сторонах AB и CD так, что отрезок KL параллелен основаниям и делит высоту трапеции в отношении 2:5, считая от меньшего основания. Найти площадь трапеции AKLD, если площадь треугольника ACD равна 63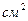 
.
№С31.13) В трапеции ABCD основания BC=3 см, AD=10 см. Отрезок KL, концы которого лежат на боковых сторонах AB и CD, параллелен основаниям, и BK:KA=3:4. Найти площадь трапеции AKLD, если площадь трапеции ABCD равна 45,5 .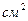
Ответы к главе 31. №31.11)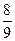 
; №31.12) 65 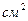; №31.13) 32.