Первая, вторая и третья задачи поиска, состояние решения, проблемы.

Суть первой задачи поиска заключается в том, чтобы найти состояние (состояния), соответствующие цели в заданном пространстве поиска. Для выполнения этой задачи вполне достаточно применить схему поиска, представленную на рисунке 1.1. Результатом решения первой задачи является найденное состояние (состояния), соответствующие цели. В зависимости от организации пространства состояний и используемого способа генерации, задача может быть решена с теми или иными ресурсными затратами. Для решения этой задачи может быть применен управляемый и неуправляемый вид поиска, осуществляемый в однонаправленном и n -направленном режимах. Отсутствие ограничений к применению базовых процедур поиска для решения задачи поиска состояния, и отсутствие требований к использованию каких-то дополнительных процедур, позволяет отметить, что эта задача поиска является относительно простой, и может быть выполнена любым методом поиска.

2) Следующая задача поиска заключается в определении места расположения целевого состояния (состояний) в пространстве поиска. Эта задача поиска заключает в себе двойственный смысл. С одной стороны, задача определения «расположения» целевого состояния может трактоваться как задача определения расстояния от начального до целевого состояния. С другой стороны, задача может быть интерпретирована как задача выделения пути от начального до целевого состояния. По сути, задача определения расстояния и задача выделения пути являются различными. Это существенное различие также подтверждается тем, что для их решения используются методы поиска с принципиально различной организацией.

Для определения расстояния до целевого состояния уже не достаточно использовать схему поиска с применением только базовых процедур представленную на рисунке 1.1. Эта схема должна быть усложнена в части процедуры проверки путем сохранения апостериорной информации о ходе поиска. Например, в памяти: M^S поисковой системы может быть сохранена последовательность операторов F_i и/или текущие оригинальные состояния S^c. Как это показано на рисунке 1.4.

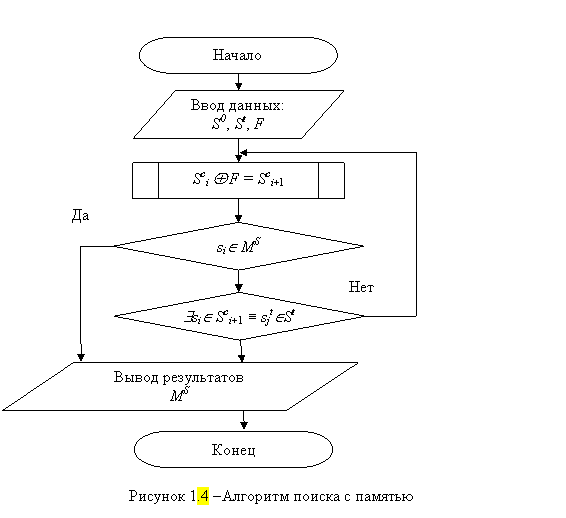
Для выделения оптимального пути от начального состояния до целевого также недостаточно использовать схему поиска, представленную на рисунке 1.1. Эта схема должна быть усложнена в части процедуры выбора перспективного текущего состояния на всех итерациях поиска. Такой выбор состояний, через которые пройдет путь, обычно выполняется на основе априорной информации. В этом случае априорная информация используется как критерий оптимальности при выборе состояний, составляющих оптимальный путь. Обычно в методах поиска ориентированных на решения задачи по выделению оптимального пути, априорная информация представлена в оценочной функции. При достижении целевого состояния цепочка операторов вида: < L_i = { f ₁ , f ₂ ,..., f_n }> представляет собой искомый путь от начального состояния до целевого состояния, оптимальный относительно заданной оценочной функции. На рисунке 1.5 представлен алгоритм поиска на основе оценочной функции f (x).

Для решения задачи выделения оптимального пути может быть использован управляемый вид поиска, осуществляемый обычно в однонаправленном режиме.

3) Следующей задачей поиска является задача преследования цели. Эта задача поиска, так же как и предыдущая задача, заключает в себе двойственный смысл.

С одной стороны под целью преследования может быть указано определенное состояние (состояния), изменяющие свое расположение в пространстве поиска. Преследование цели обычно выполняется с помощью традиционного метода «погони», метода с постоянным или переменным углом опережения, методом параллельного и пропорционального сближения. Каждый класс методов преследования цели обладает свойственными ему достоинствами и недостатками. В конкретном случае выбор того или иного метода преследования цели определяется относительно скорости работы поисковой системы, направления и скорости перемещения цели, от объема и точности априорной и текущей апостериорной информации. Для реализации методов преследования цели используется управляемый поиск, осуществляемый в однонаправленном и n -направленном режимах.

С другой стороны преследование цели может быть интерпретировано как исследование и/или анализ изменений свойств состояний пространства поиска. Для решения этой задачи обычно применяют метод полного перебора состояний пространства поиска (breadth-first pro­cess). Практически все методы поиска, представленные в [1-5,7,8] прекращают поиск, как только достигается целевое состояние, определяется расстояние или выделяется путь. Суть задачи полного перебора заключается в определение модели организации пространства поиска и/или распределения целевых состояний. Например, модели должны позволить определить вид и динамику изменения распределения состояний в пространстве поиска. Модель целевых состояний может быть представлена в виде оценки плотности распределения состояний в пространстве поиска. По этой причине для реализации метода полного перебора использование алгоритма поиска, представленного на рисунке 1.1, недостаточно. Для реализации метода полного перебора необходимо априори задать цель исследования и/или анализа. Для решения этой задачи следует использовать управляемый вид поиска, осуществляемый обычно в однонаправленном режиме.

Первая задача: Поиск состояния, нескольких заданных, всех состояний S^t на дереве или графе из одного, нескольких заданных, всех состояний S^o.

Вторая задача: Определение расстояния, т.е. ограничение направления поиска или граничной глубины поиска: H_i, до заданного состояния, нескольких заданных, всех состояний S^t на дереве или графе из одного, нескольких заданных, всех состояний S^o.

Третья задача: Выделение оптимального пути как цепочки: L_i = (f ₁, f ₂, …, f_n), до заданного состояния, нескольких заданных, всех состояний S^t на дереве или графе из одного, нескольких заданных, всех состояний S^o;