Выполнение второго задания.

3.1. Вычислим точечные и интервальные оценки математического ожидания (выборочного среднего значения) и дисперсии (выборочной исправленной дисперсии) по данным таблиц 1 и 2. сначала определим точечные оценки.

Интервальную оценку математического ожидания (доверительный интервал) при заданной доверительной вероятности (надежности) и числе наблюдений (объеме выборки) n =100 определим по формуле:

,

где - точность вычисления МО по результатам наблюдений при заданных значениях n и . 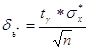, где определяется по таблицам Стьюдента:

= =1,984

Интервальная оценка (доверительный интервал) для МО равна:

Этим отрезком с вероятностью 0,95 накрывается истинное (неизвестное) значение МО.

Интервальная оценка среднего квадратического отклонения (доверительный интервал) определяется по формуле:

,

где q определяется по таблице

q = q(100;0,95)=0,143

Доверительный интервал для оценки с.к.о. равен

42,493(1-0,143)< <42,493(1+0,143)

36,42< <48,57

Этим отрезком с вероятностью 0,95 накрывается истинное (неизвестное) значение с.к.о.

3.2. На основании изучения гистограммы (рис.3) выдвинем гипотезу о нормальном распределении генеральной совокупности случайных величин X - трудозатрат на доработки на объекте. Нулевую гипотезу подвергнем статистической проверке на противоречивость данным, полученным из опыта (табл.1) по критериям - Пирсона и - Колмогорова.

В соответствии с методом моментов положим параметры нормального распределения равным оценкам:

3.3. На графиках гистограммы и эмпирической функции распределения (рис.1,3) построим сглаживающие функции (теоретические кривые) плотности вероятности и функции распределения в соответствии с их выражениями:

Для построения сглаживающих кривых используем таблицы нормированной нормальной плотности вероятности

и нормированной нормальной функции распределения

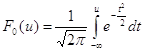
Для входа в таблицы нормируем случайную величину Х по формуле:

Значения нормированных величин на границах разрядов, численные значения сглаживающих кривых на границах разрядов приведены в таблице 6.

Таблица 6

Границы разрядов
	-2,92	-1,98	-1,04	-0,10	0,84	1,78	2,73
	0,0056	0,0562	0,2341	0,3970	0,2803	0,0818	0,0096
	0,013	0,132	0,55	0,93	0,66	0,19	0,023
		0,024	0,14917	0,4602	0,79955	0,96246	0,99683

3.4. Статистическую проверку гипотезы о нормальном распределении случайной величины Х по выборке из 100 значений осуществим по двум различным критериям.

1) Критерий - Пирсона.

Суммарная выборочная статистика - Пирсона рассчитывается по результатам наблюдений по формуле:

,

где - числа попаданий значений х в j – й разряд (табл.3);

n – число наблюдений (объем выборки);

m – число разрядов;

- вероятность попадания случайной величины Х в j – й интервал, вычисляемая по формуле:

,

где , - границы разрядов;

Ф(u) – функция Лапласа.

Результаты расчетов выборочной статистики приведены в таблице 7.

Таблица 7

№		[280..320]	(320..360]	(360..400]	(400..440]	(440..480]	(480..520]
		0,0221	0,1276	0,3087	0,3393	0,1602	0,0421
		2,21	12,76	30,87	33,93	16,02	4,21
	-	-0,21	-2,76	5,13	-0,93	-2,02	0,79
		0,0441	7,6176	26,3169	0,8649	4,0804	0,6241
	<5>:<3>	0,02	0,597	0,853	0,025	0,2547	0,1482

Проверяем гипотезу о нормальном распределении генеральной совокупности значений Х:

1). По таблице - распределения по заданному уровню значимости =0,10 и числу степеней свободы k=m-2-1=3 (m=6 – число разрядов, 2 – число параметров нормального распределения ) определим критическое значение , удовлетворяющее условию:

.

В нашем случае

2). Сравнивая выборочную статистику , вычисленную по результатам наблюдений, с критическим значением , получаем:

,

< - согласуется с данными опыта (принимается).

Вывод: статистическая проверка по критерию - Пирсона нулевой гипотезы о нормальном распределении значений х генеральной совокупности, выдвинутой на основании выборочных данных, не противоречит опытным данным.

2). Критерий - Колмогорова.

Выборочная статистика - Колмогорова рассчитывается по формуле:

где

модуль максимальной разности между эмпирической и сглаживающей функциями распределения.

При заданном уровне значимости =0,10 критическое значение распределения Колмогорова Полученной на основании выражения:

функции распределения статистики - Колмогорова.

Для проверки нулевой гипотезы проведем следующую процедуру:

1). Найдем максимальное значение модуля разности между эмпирической и сглаживающей F(x) функциями распределения:

=0,063.

2). Вычислим значение выборочной статистики по формуле:

=0,063 =0,63.

3). Сравнивая выборочную статистику и критическое значение получаем:

=0,63<1,224= .

Следовательно, гипотеза о нормальном распределении случайной величины Х согласуется с опытными данными.

3.5. Вероятность попадания значений случайной величины Х на интервал [МО - с.к.о.; МО + 2*с.к.о.] вычислим по формуле:

P=(X [404,180-42,493;404,180+2*42,493])=P(X [361,7;489,17])=

= =Ф(2)+ Ф (1)=

=0,477+0,341=0,818.

ЛИТЕРАТУРА

Монсик В.Б. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: Пособие к выполнению курсовой работы. – М.: МГТУ ГА, 2002. – 24 с..