ЦЕНТРАЛЬНЫЙ ФИЛИАЛ
 |
Кафедра правовой информатики, информационного права
И естественнонаучных дисциплин
Утверждаю
Зам. директора по учебной
и воспитательной работе
к.в.н., доцент
В.Д. Ерёменко
31 августа 2011 г.
ПЛАН
Практического занятия
Дисциплина: «Информационные технологии в юридической деятельности».
Тема 4.1: «Множества и операции над ними».
Разработал:
заведующий кафедрой
к.т.н., доцент
А.В. Мишин
Материалы обсуждены и одобрены
на заседании кафедры ПИИПЕД,
протокол № 1 от «29 » августа 2011 г.
Воронеж - 2011
План проведения занятия
Тема № 4: «Основные закономерности создания информационных процессов».
Занятие № 1: «Множества и операции над ними».
| Учебные вопросы | Время, мин |
| Вступительная часть.................................... 1. Понятие и способы задания множества.................... 2. Операции над множествами............................. Заключительная часть................................... |
Литература:
основная:
1. Мишин А.В. Информатика и математика: учебное пособие / А.В. Мишин, Л.Е. Мистров, А.Ю. Кузьмин. – Воронеж: Научная книга, 2006. – С. 6-9, 16-19.
дополнительная:
2. Турецкий В.Я. Математика и информатика: Учебник / В.Я. Турецкий. – 3-е изд., испр. и доп. – М.: ИНФРА-М, 2002. – С. 21-35.
Содержание занятия и методика его проведения
Вступительная часть. Преподаватель проверяет наличие и готовность студентов к проведению занятия, делает соответствующие записи в журнале. Объявляется тема, цель и план проведения занятия. Акцентируется внимание студентов на важности изучаемой темы для усвоения последующего материала учебной дисциплины.
Основная часть. Преподаватель проверяет усвоение студентами ранее изученного учебного материала и выполнение ими домашнего задания. Доводит основные теоретические сведения и организует выполнение заданий по теме.
Заключительная часть. В заключительной части практического занятия преподаватель подводит итоги, отмечает ошибки в действиях студентов, оценивает работу и отвечает на их вопросы, выдаёт задание на самоподготовку.
Задание на самоподготовку. К следующему практическому занятию:
1) повторить содержание операций над множествами;
2) письменно выполнить следующие задачи.
Задача 1. Даны множества 
и 
. Найти: а) А È В; б) А Ç В; в) В \ А; г) A D B.
Задача 2. Заданы множества A = {2, 4} и B ={1, 5, 7}. Найти декартово произведение множеств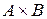 
.
Задача 3. Представить диаграммы Эйлера-Венна множеств:
а) 
;
б) 
;
в) 
.
Тема 4.1. Множества и операции над ними
Цель занятия – изучить первичные понятия теории множеств, необходимые для последующего восприятия закономерностей создания информационных процессов.
Теоретические сведения
Понятие и способы задания множества
Понятие множества так же, как и понятия точки, числа и т.д., является одним из наиболее общих понятий, для которых нет строгого определения. Мы можем лишь, в какой-мере объяснить такое понятие, описав его основные свойства.
Кантор описывает множество следующим образом.
Множество есть любое собрание определённых и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое.
Все объекты, входящие во множество, обладают тремя важными свойствами. Во-первых, они мыслятся как единое целое. Во-вторых, они отличимы друг от друга. И, в-третьих, для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет.
Множества обычно обозначают прописными буквами латинского алфавита: А, В, С,..., Z. Примерами множеств являются: множество студентов Российской академии правосудия, множество судов и т.п.
Объекты, составляющие множество, называются его элементами или точками и обозначаются строчными буквами латинского алфавита: a, b, c, …, z.
То, что элемент а входит в множество А, записывается так: а Î А (читается: а есть элемент множества А или а принадлежит множеству А). Запись а Ï А означает, что элемент а не принадлежит множеству А.
Различают конечные множества и бесконечные.
Конечное множество состоит из конечного числа элементов.
Число элементов в конечном множестве А называют мощностью (или кардинальным числом) и обозначают 
.
Количество элементов в бесконечном множестве подсчёту не поддаётся.
Термин «множество» употребляется независимо от того, много или мало в этом множестве элементов.
Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Æ.
Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:
1. Перечислением элементов: А = { а 1, а 2, …, аk }. Например, множество студентов в учебной группе задаётся перечислением фамилий в журнале учёта занятий. Это нетрудно сделать, так как такое множество содержит конечное число элементов. Однако не всякое конечное множество можно задать перечислением. Множества птиц на нашей планете или рыб в океане тоже конечные, но попробуйте их перечислить (или пересчитать)! Тем более нельзя перечислить все элементы бесконечного множества.
2. Характеристическим свойством: А = { а ½ Р (а)}. Характеристическое свойство (предикат) – это некоторое условие Р, выраженное в форме логического утверждения относительно элемента а. Если для данного элемента а условие выполнено, то он принадлежит определяемому множеству А, в противном случае – а Ï А.
3. Порождающей процедурой: А = { а ½ а: = f }. Порождающая процедура – это процедура f, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества. Например, процедура расследования уголовного преступления предусматривает подбор множества свидетелей, представляемых стороной обвинения в ходе последующего судебного разбирательства.
Если каждый элемент множества А является в то же время элементом множества В, то говорят, что А - подмножество в множестве В (или В включает А), и пишут А Ì В.
Приведём примеры подмножеств: множество студентов 1 курса Центрального филиала РАП есть подмножество всех студентов этого филиала; множество гражданско-правовых исков есть подмножество всех исков, входящих в компетенцию судов общей юрисдикции.
Если одновременно с отношением А Ì В имеет место отношение В Ì А, то такие два множества равны: А = В, т. е. А и В состоят из одних и тех же элементов.
Для наглядной иллюстрации множеств удобно пользоваться так называемыми диаграммами Эйлера-Венна.
Диаграмма Эйлера-Венна - это замкнутая линия, внутри которой расположены элементы данного множества.
Пример диаграммы множества А = { а 1, а 3, а 7} изображён на рис. 4.1. Отношение А Ì В изображено с помощью диаграммы на рис. 4.2.
Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества Е (своего для каждого случая), которое называется универсальным множеством(или универсумом).
В качестве примера возьмём множество книг. В это множество входят подмножества научных, художественных книг, книг по искусству. Среди научных книг есть подмножества книг по математике, информатике, юриспруденции и т. д. Множество всех книг - это универсальное множество, содержащее в себе очень много различных подмножеств книг.
Рис. 4.1Рис. 4.2
Для информационных процессов важную роль играют числовые множества – множества, элементами которых являются действительные числа. Напомним известные вам из школьного курса алгебры сведения.
Целыми называются числа 0, ±1, ±2, …. Множество целых чисел принято обозначать буквой Z = {…, -2, -1, 0, 1, 2, …}.
Натуральные числа – целые положительные числа. Множество натуральных чиселпринято обозначать буквой N = {1, 2, 3, …}.
Простые числа – натуральные числа, большее, чем единица, и не имеющее других делителей, кроме самого себя и единицы. Множество простых чисел будем обозначать буквой P = {2, 3, 5, 7, 11, 13,…}.
Числа целые и дробные, как положительные, так и отрицательные, вместе с числом нуль называются рациональными числами. Множество рациональных чиселпринято обозначать буквой Q.
Каждое рациональное число может быть представлено в виде отношения двух целых чисел p и q, например,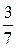 
, 
. В частности, целое число p можно рассматривать как отношение двух целых чисел 
, например 
, 
.
Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей.
Числа, которые представляются бесконечными, но непериодическими дробями, называются иррациональными числами: таковы числа 
, 
, 
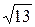и т.д. Множество иррациональных чиселпринято обозначать буквой I. Совокупность всех рациональных и иррациональных чисел называется множеством действительных (или вещественных) чисел R = (
).
Действительные числа упорядочены по величине, т.е. для каждой пары действительных чисел х и у имеет место одно, и только одно, из соотношений:
x < y, x = y, x > y.
Очевидно, что 
, 
.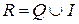