1. Докажите, что P 2 + Q2 делится нацело на 3 Û P 2 + Q2 делится нацело на 9.
2. Существует ли четверка целых чисел такая, что х 2 + у 2 = 3(z 2 + u 2)?
3. ** Докажите, что P 2 + Q2 делится нацело на 21 Û P 2 + Q2 делится нацело на 441.
4. Решите в натуральных числах уравнения: а) 19х+97y = 1997, б) 20x + 13y = 2013; в) 7x – 9y = 100; г) X2-Y2=31; А в целых?
5. Решите уравнение 3 х + 5 у = 7 в целых числах (а в натуральных числах).
6. Решите уравнение 3 х – 12 у = 7 в целых числах.
7. Решите уравнение 90 х – 3 у = 12 в целых числах (а в натуральных числах).
8. Решите уравнение 1990 х – 173 у = 11 в целых числах.
9. Решите уравнение 21 х + 48 у = 6 в целых числах.
10. а) (2 х + у)(5 х +3 у) = 7, б) (х + у)(3 х +3 у) = 7, в) (3 х + 4 у)(4 х +3 у) = 49.
11. а) ху = х + у + 3. б) 3 ху – х – у = 1.
12. а) х 2 = 14 + у 2. б) х 2 + у 2 = х + у + 2.
13. а) х 2 – 7 у = 10. б) х 3 + 21 у 2 + 5 = 0, в) 15 х 2 – 7 у 2 = 9.
14. 3 т + 7 = 2 п. 2 или 3 идеи!!!
15. Ученик решает задание из 20 задач. За верно решенную задачу ему ставят 8 баллов, за неверно решенную (-5) баллов, за задачу, которую не брался решать – 0 баллов. Сколько задач он брался решать, если в сумме он получил 13 баллов?
16. Профессор Потапов меняет шило на мыло, академик Агатов 4 мыла на 1 шило, а доцент Долматов 1 мыло на 5 шила (но не наоборот). После нескольких обменов у студента Сидорова оказалось столько же шила и мыла, сколько было вначале. Докажите, что количество сделанных обменов делится на 26. Развитие идеи!!!
17. В стоэтажном доме в лифте работают всего две кнопки: подняться на 7 этажей вверх и опуститься на 5 этажей вниз. Можно ли с первого этажа подняться на 77-й? А опуститься? А переехать с любого этажа на любой другой?
18. В банке 500 долларов. Разрешаются две операции: взять из банка 300 долларов или положить в него 198 долларов. Эти операции можно проводить много раз, при этом, однако, никаких денег, кроме тех, что первоначально лежат в банке, нет. Какую максимальную сумму можно извлечь из банка и как это сделать? Алгоритм!!!
19. Найдите наименьшее натуральное число, которое не менее чем четырьмя различными способами можно представить в виде 
, где m и n – натуральные числа.
20. * Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 2014? *** Если да, найдите наименьшие такие числа.
9 класс - № 1. Найдите все пары (a; b) натуральных чисел a и b, удовлетворяющие следующим двум условиям: 1) остаток от деления числа 2 a на число b равен 7,
2) остаток от деления числа 2 b на число a равен 17
9 класс - № 2. Квадратный трехчлен 
с натуральными коэффициентами a, b и с имеет два различных целых корня. Известно, что 
, где р – некоторое натуральное простое число. Найдите все возможные значении суммы 
.
2016 год, 8 класс (3-й этап, второй день): Найдите все целые значения n, при которых дробь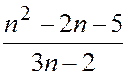 
является целым числом. Развитие некоторых предыдущих идей!!!
2018 год, 8 класс (3-й этап, первый день): Найдите все возможные пары натуральных чисел a и b, для которых дробь 
также является натуральным числом. Еще развитие идеи!!!
А может здесь доклад Безрукова!!!
И далее возможно
Турнир Городов, сложный тур, 6-7 класс
У Васи есть две «печати-тримино», или, другими словами, печати, черные красящие поверхности которых имеют вид двух тримино: полоски и уголка, состоящих из трех клеток.
а) Может ли Вася, используя только печать в виде полоски и приложив ее несколько раз к листу бумаги, получить клетчатый квадрат 8´8, все клетки которого, кроме одной угловой, черные? (Накладывать один отпечаток на другой не разрешается.)
б) Тот же вопрос для клетчатого квадрата 16´16 (вновь без одной угловой клетки).
в) Тот же вопрос для клетчатого квадрата 16´16 без одной угловой клетки, но с использованием только печати в виде уголка?
и общая задача на разрезания
0. Докажите, что любой треугольник является правильным (равносторонним).
и теперь геометрический блок (от известных (?!) свойств дуг, углов, касательных, секущих к новым свойствам, часто через анализ и исследование, а потом догадку)
1.(легкая, но важная) АВСD – выпуклый четырехугольник, О – точка пересечения его диагоналей. Докажите, что SABO = SCDO тогда и только тогда, когда ABCD является трапецией (возможно, параллелограммом).
2. Докажите, что неравнобедренный треугольник является прямоугольным тогда и только тогда, когда найдется такая его вершина, что проведенная из нее биссектриса треугольника является также биссектрисой угла, образованного медианой и высотой треугольника, выходящими из этой вершины.
3. (интересная и красивая) Равнобедренный треугольник АВС, боковые стороны которого АВ и ВС, вписан в окружность W. Другая окружность касается стороны ВС в точке С, пересекает основание треугольника АС в точке К, а окружность W в точке Н. Докажите, что точки В, К и Н лежат на одной прямой.
4. На окружности даны точки А, В, С, D в указанном порядке; 
– середины дуг АВ, ВС, СD, DА соответственно. Докажите, что 
5. (Минская городская интернет-олимпиада 2019, 8 класс) Вне равностороннего треугольника ABC отмечены точки S и T такие, что Ð SAB = Ð TCA = 45° и Ð SBA = Ð TAC = 15°.
а) Докажите, что ST = AB. б) Найдите угол между прямыми ST и AB. (Два решения)
6. На окружности даны точки А, В, С, D в указанном порядке. М – середина дуги АВ. Обозначим точки пересечения хорд (прямых) МС и МD с хордой (прямой) АВ через Е и К. Докажите, что КЕСD – вписанный четырехугольник. (А на какой дуге лежит точка М??)
7. O – точка пересечения диагоналей параллелограмма ABCD. Докажите, что если окружность, проходящая через точки A, B и O, касается прямой BC, то окружность, проходящая через точки B, C и O, касается прямой CD. ( два решения!)
8. На продолжении стороны BC треугольника ABC за вершину B отложен отрезок BB ', равный стороне AB. Биссектрисы внешних углов при вершинах B и C пересекаются в точке M. Докажите, что точки A, B', M и C лежат на одной окружности.
9. Пусть AK, BM и CP – высоты остроугольного треугольника ABC, а L, N и Q – точки пересечения продолжений этих высот с окружностью, описанной вокруг DABC. Чему может быть равно численное значение выражения 
? (здесь используются два (!) важных свойства)
10. (Турнир Городов, сложный тур, 8-9 класс) Из центра О описанной окружности треугольника АВС опустили перпендикуляры ОР и ОQ на биссектрисы внутреннего и внешнего углов при вершине В. Докажите, что прямая PQ делит пополам отрезок, соединяющий середины сторон СВ и АВ. (КЛАСС!!!)
11. В треугольнике АBС точка Н – ортоцентр (точка пересечения высот). Прямая, проходящая через точку Н перпендикулярно высоте СН, пересекает окружность, описанную около треугольника ВНС в точке К. Докажите, что АВКН – параллелограмм.
12. Три окружности одного и того же радиуса r пересекаются в точке М и, кроме того, попарно пересекаются в точках A, B, C. Найдите радиус окружности, описанной вокруг треугольника АВС.
13. (Турнир Городов, базовый тур, 8-9 класс) Дана окружность ω с центром O и две её различные точки A и C. Для любой другой точки P на ω отметим середины X и Y отрезков AP и CP и построим точку H пересечения высот треугольника OXY. Докажите, что положение точки H не зависит от выбора точки P.
А здесь работу по самопересекающимся многоугольникам и построениям с помощью двусторонней линейки!!!