Задания 16. Решение задач разных типов
Задание 16 № 16
Первый участок пути протяженностью 120 км автомобиль проехал со скоростью 80 км/ч, следующие 75 км — со скоростью 50 км/ч, а последние 110 км — со скоростью 55 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Запишите решение и ответ.
Решение.
Всего автомобиль проехал: 120 + 75 + 110 = 305 (км), затратив на весь путь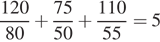 
(ч).
Таким образом, средняя скорость: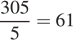 
(км/ч).
Допускается другая последовательность действий и рассуждений, обоснованно приводящая к верному ответу.
Ответ: 61 км/ч.
Задание 16 № 1092
Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение.
Пример всю работу за 1. Пусть первый оператор за 1 час выполняет x частей работы, а второй — y частей. При совместной работе производительности складываются. Составим систему уравнений:
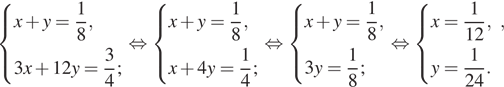
Значит, первый оператор выполняет работу за 12 часов, а второй за 24 часа.
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.
Задание 16 № 1093
Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км. Далее скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля. Таким образом, первый автомобиль до встречи находился в пути 8 часов и проехал за это время 400 километров.
Ответ: 400 км.
Задание 16 № 1094
Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
За первый час пути автомобиль, выехавший из города А, проехал 55 километров, и расстояние от него до города В стало равным 435 км. Далее скорость сближения двух автомобилей равна 145 км/ч, значит, они встретятся через 3 часа после выезда второго автомобиля. Таким образом, первый автомобиль до встречи находился в пути 4 часа и проехал за это время 220 километров.
Ответ: 220 км.
Задание 16 № 1095
Железнодорожный состав длиной в 1 км прошёл бы мимо столба за 1 мин., а через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)?
Решение.
Поезд проходит через туннель за 3 минуты, при этом за одну минуту поезд проходит мимо выхода из туннеля, следовательно, от входа локомотива в туннель до выхода проходит 2 минуты. Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км/мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км.
Ответ: 2.
Задание 16 № 1096
Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Решение.
Пусть x — количество вопросов теста. Тогда получаем:
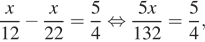
откуда находим x = 33.
Ответ: 33.
Задание 16 № 1097
Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию, первая труба за одну минуту наполняет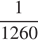 
часть бассейна, а две трубы вместе за одну минуту наполняют 
часть бассейна. Таким образом, одна вторая труба за минуту наполняет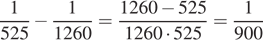 
часть бассейна, то есть она наполнит весь бассейн за 15 часов.
Ответ: 15.
Задание 16 № 1098
Две трубы наполняют бассейн за 6 часов 18 минут, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию, первая труба за одну минуту наполняет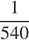 
часть бассейна, а две трубы вместе за одну минуту наполняют 
часть бассейна. Таким образом, одна вторая труба за минуту наполняет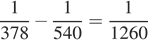 
часть бассейна, то есть она наполняет весь бассейн за 21 час.
Ответ: 21.
Задание 16 № 1099
Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.
Решение.
Пусть длина поезда l м. Скорость поезда относительно пешехода равна 63 − 3 = 60 км/ч, или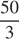 
м/с. Следовательно, поезд проезжает мимо идущего в том же направлении параллельно путям пешехода за l: 
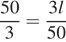секунд.
Составим и решим уравнение:
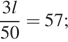
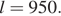
Длина поезда составляет 950 м.
Ответ: 950 м.
Задание 16 № 1100
Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 5 км/ч пешехода за 45 секунд. Найдите длину поезда в метрах.
Решение.
Пусть длина поезда l м. Скорость поезда относительно пешехода равна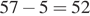 
км/ч, или 
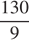м/c. Следовательно, поезд проезжает мимо идущего в том же направлении параллельно путям пешехода за l: 
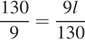секунд.
Составим и решим уравнение: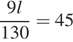 
; 
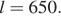Длина поезда составляет 650 м.
Ответ: 650 м.
Задание 16 № 1101
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 30 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 144 км, скорость первого велосипедиста равна 24 км/ч, скорость второго — 28 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Решение.
За то время, пока первый велосипедист делал остановку, второй велосипедист проехал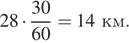 
Всё остальное время они одновременно находились в пути, значит, второй велосипедист за это время проехал 
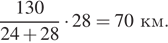Таким образом, суммарно он проехал 84 км.
Ответ: 84 км.
Задание 16 № 1102
Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение.
Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь. За первые 5 часов автомобиль проехал 5 · 60 = 300 км, за следующие три часа — 3 · 100 = 300 км и за последние 4 часа — 4 · 75 = 300 км. Весь путь составил 300 + 300 + 300 = 900 км, а суммарное время движения — 5 + 3 + 4 = 12 часов, откуда средняя скорость автомобиля на протяжении всего пути 900/12 = 75 км/ч.
Ответ: 75.
Задание 16 № 1104
Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение.
Обозначим выполняемую мальчиками работу по покраске забора за 1. Пусть за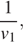 
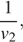
часов Игорь, Паша и Володя соответственно покрасят забор, работая самостоятельно. Игорь и Паша красят забор за 20 часов:
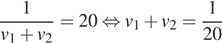
Паша и Володя красят этот же забор за 24 часа:
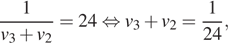
а Володя и Игорь — за 30 часов:
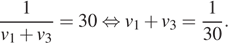
Получаем систему уравнений:
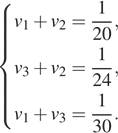
Просуммируем левые и правые части данных трех уравнений, получим:
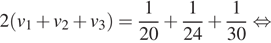
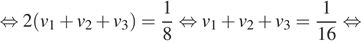
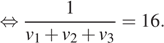
Ответ: 16.
Приведём другое решение.
За один час Игорь и Паша красят 1/20 забора, Паша и Володя красят 1/24 забора, а Володя и Игорь — за 1/30 забора. Работая вместе, за один час два Игоря, Паши и Володи покрасили бы:
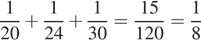забора.
Тем самым, они могли бы покрасить один забор за 8 часов. Поскольку каждый из мальчиков был учтен два раза, в реальности Игорь, Паша и Володя могут покрасить забор за 16 часов.