106. Задание {{ 25 }} ТЗ № 25
Случайную вариацию отражает
£ изменение массовых явлений во времени
£ общая дисперсия
£ межгрупповая дисперсия
R внутригрупповая дисперсия
107. Задание {{ 26 }} ТЗ № 26
Модой в ряду распределения является
£ наибольшая варианта
£ наибольшая частота
£ варианта, делящая ряд распределения значений на две равные части
R варианта, которая чаще других встречается
108. Задание {{ 27 }} ТЗ № 27
Средняя величина характеризует
£ динамику разных социально-экономических явлений
£ зависимость между единицами совокупности
£ уровень вариации явления
R уровень развития явления в целом по совокупности при большом количестве наблюдений
109. Задание {{ 28 }} ТЗ № 28
Если вариационный ряд имеет следующий вид
x 30 40 50
m 2 5 3
то мода равна....... (ввести ответ)
Правильные варианты ответа: 40;
110. Задание {{ 29 }} ТЗ № 29
В теории статистики для расчета межгрупповой дисперсии по правилу сложения дисперсий используют следующие данные
R средняя из внутригрупповых дисперсий
£ среднее значение признака
£ размах вариации
R общая дисперсия
111. Задание {{ 30 }} ТЗ № 30
Коэффициент детерминации изменяется в пределах
R от 0 до 1
£ всех положительных чисел
£ от -1 до 1
£ от -1 до 0
112. Задание {{ 31 }} ТЗ № 31
В теории статистики объективность и типичность статистической средней обеспечивается, если статистическая совокупность соответствует следующим требованиям
R достаточно большой объем единиц наблюдения
R качественная однородность
£ имеет небольшой объем единиц наблюдения
£ содержит существенно различные единицы наблюдения
113. Задание {{ 32 }} ТЗ № 32
Для определения общей средней из групповых средних (удельный вес групп неодинаков) следует применить формулу средней
£ арифметической простой
£ гармонической простой
R арифметической взвешенной
£ гармонической взвешенной
114. Задание {{ 33 }} ТЗ № 33
Квартиль - это
R значение признака, делящее ранжированную совокупность на четыре равные части
£ варианта, занимающая определенное место в ранжированном вариационном ряду
£ значение признака, делящее ранжированную совокупность на десять равных частей
£ значение признака, делящего ранжированную совокупность на пять равных частей
115. Задание {{ 34 }} ТЗ № 34
Средняя величина характеризует
£ каждую конкретную единицу
R всю совокупность в целом одним числом
£ варианту, стоящую в середине ранжированного ряда
£ объем вариационного ряда
116. Задание {{ 35 }} ТЗ № 35
Сумма отклонений индивидуальных значений признака от средней арифметической равна
R нулю
£ любому числу в зависимости от исходных данных
£ единице
£ десяти
117. Задание {{ 36 }} ТЗ № 36
Если частоты всех значений признака уменьшить в два раза, то значение средней
£ уменьшится
R не изменится
£ предсказать невозможно
£ увеличится
118. Задание {{ 37 }} ТЗ № 37
Согласно правилу мажорантности средняя арифметическая больше средней
£ квадратической
£ кубической
R гармонической
£ хронологической
119. Задание {{ 38 }} ТЗ № 38
В теории статистики для расчета общей дисперсии по правилу сложения дисперсий используются следующие данные
R межгрупповая дисперсия
£ среднее квадратическое отклонение
R средняя из внутригрупповых дисперсий
£ среднее значение признака
120. Задание {{ 39 }} ТЗ № 39
В статистической практике значение моды дискретного признака не может быть определено в следующих случаях
£ признак имеет нормальный закон распределения
R совокупность на имеет повторяющихся значений признака
£ данные представлены в виде вариационного ряда
R вариация признака отсутствует
121. Задание {{ 40 }} ТЗ № 40
Имеются следующие данные о лабораторных испытаниях 1000 образцов пряжи на крепость
Крепость
пряжи до 180 180-200 200-220 220-240 240 и более
Число
образцов 60 150 440 250 100
Средняя крепость пряжи равна
£ 208,7
£ 220,0
£ 210,0
R 213,6
122. Задание {{ 41 }} ТЗ № 41
Вывод о вариации индивидуального значения признака вокруг среднего его значения в среднем на 10% сделана на основе
£ среднего квадратического отклонения
£ размаха вариации
R коэффициента вариации
£ коэффициента осцилляции
123. Задание {{ 42 }} ТЗ № 42
Количество наблюдений случайной величины находящихся в интервале трех сигм равно
£ 68,3 %
R 99,7 %
£ 95,4 %
£ 90,0 %
124. Задание {{ 43 }} ТЗ № 43
Согласно теории статистики децильный коэффициент, применяемый для оценки дифференциации доходов населения, соответствует следующим утверждениям
R характеризует соотношение минимальных доходов 10% богатых и максимальных доходов 10% бедных
£ характеризует разность минимальных доходов 10% богатых и максимальных доходов 10% бедных
R может принимать положительные значения
£ изменяется от -1 до 1
125. Задание {{ 44 }} ТЗ № 44
Для расчета дисперсии используются формулы
£ средняя арифметическая простая из модулей отклонений значений признака от средней величины
R средняя арифметическая простая из квадратов отклонений значений признака от средней величины
£ средняя арифметическая взвешенная из модулей отклонений значений признака от средней величины
R средняя арифметическая взвешенная из квадратов отклонений значений признака от средней величины
126. Задание {{ 225 }} ТЗ № 225
Согласно теории статистики нормальному распределению соответствуют следующие утверждения
£ показатель эксцесса больше единицы
R показатель эксцесса равен нулю
R показатель асимметрии равен нулю
£ показатель асимметрии равен единице
127. Задание {{ 171 }} ТЗ № 171
К относительным показателям вариации относят
R относительное линейное отклонение
R коэффициент вариации
£ среднее линейное отклонение
£ размах вариации
128. Задание {{ 172 }} ТЗ № 172
В теории статистики показатель "коэффициент осцилляции" характеризует следующие утверждения
£ отношение размаха вариации к минимальному значению признака
£ абсолютный показатель вариации
R отношение размаха вариации к среднему значению признака
R относительный показатель вариации
129. Задание {{ 173 }} ТЗ № 173
Согласно теории статистики для вычисления дисперсии альтернативного признака используют следующие данные
£ доля распределения признака, частости
R доля единиц, обладающих признаком
R доля единиц, не обладающих признаком
£ значения признака
130. Задание {{ 174 }} ТЗ № 174
В теории статистики согласно правилу сложения дисперсий справедливы следующие утверждения
£ средняя из групповых дисперсий равна сумме общей дисперсии и межгрупповой дисперсии
£ общая дисперсия равна разности межгрупповой дисперсии и средней из групповых дисперсий
R общая дисперсия равна сумме межгрупповой дисперсии и средней из групповых дисперсий
R межгрупповая дисперсия равна разности общей дисперсии и средней из групповых дисперсий
131. Задание {{ 217 }} ТЗ № 217
Для расчета дисперсии используются формулы
£ 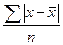
R 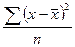
£ 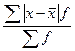
R 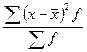
132. Задание {{ 218 }} ТЗ № 218
Для расчета среднего линейного отклонения используются формулы
£ 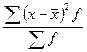
R 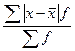
£ 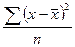
R 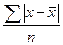
133. Задание {{ 228 }} ТЗ № 228
В теории статистики к структурным средним относят следующие показатели
R мода
£ средняя хронологическая
£ средняя арифметическая
R медиана
134. Задание {{ 229 }} ТЗ № 229
Согласно теории статистики при использовании накопленной частоты вариационного ряда справедливы следующие утверждения о том, что последняя накопленная частота равна
£ сумме накопленных частот
£ произведению накопленных частот
R количеству единиц совокупности
R единице
135. Задание {{ 232 }} ТЗ № 232
Согласно теории статистики нормальному распределению соответствуют следующие утверждения
£ мода, медиана и среднее значение признака равны нулю
R показатели асимметрии и эксцесса равны нулю
R мода, медиана и среднее значение признака равны между собой
£ показатели асимметрии и эксцесса равны единице
Индексный метод
136. Задание {{ 99 }} ТЗ № 99
Если индекс фиксированного состава составил 250 %, индекс структурных сдвигов - 150 %, то индекс цен переменного состава вырос на
£ 375 %
R 275 %
£ 166 %
£ 60 %
137. Задание {{ 100 }} ТЗ № 100
Если индекс переменного состава составил 90 %; индекс постоянного состава - 120 %, то индекс структурных сдвигов (в %) равен (Результат ввести без указания единиц измерения)
Правильные варианты ответа: 75;
138. Задание {{ 101 }} ТЗ № 101
"Идеальный" индекс Фишера по форме представляет собой
£ среднюю арифметическую
£ среднюю агрегатную
R среднюю геометрическую
£ среднюю гармоническую
139. Задание {{ 102 }} ТЗ № 102
Индекс Ласпейреса рассчитывается как отношение суммы произведений цен товаров текущего периода времени на показатели количества базисного периода к сумме произведений цен товаров на их показатели количества......... периода времени
R базисного
£ текущего
£ будущего
£ прогнозируемого
140. Задание {{ 103 }} ТЗ № 103
Влияние структурных сдвигов в объеме проданной продукции на изменение прибыли определяется с помощью
£ корреляционного метода
£ средних величин
R индексного метода
£ метода группировок
141. Задание {{ 104 }} ТЗ № 104
Индекс цен, исчисленный с весами базисного периода, является индексом цен
£ Фишера
£ Пааше
£ Стьюдента
R Ласпейреса
142. Задание {{ 105 }} ТЗ № 105
Индекс.......... выражается отношением средних величин за два периода (по двум объектам).
£ произвольного состава
R переменного состава
£ постоянного состава
£ структурных сдвигов
143. Задание {{ 106 }} ТЗ № 106
Индексом, измеряющим динамику среднего уровня экономического показателя, является
£ базисный индекс с переменными весами
R индекс переменного состава
£ индекс фиксированного состава
£ цепной индекс
144. Задание {{ 107 }} ТЗ № 107
Индекс реальных доходов населения рассчитывается как отношение индекса номинальных доходов к индексу
R потребительских цен
£ цен отраслей
£ покупательной способности денег
£ совокупных доходов
145. Задание {{ 108 }} ТЗ № 108
Индекс потребительских цен в настоящее время в России определяется по модифицированному индексу цен
R Ласпейреса
£ Пааше
£ Фишера
£ Эджворта - Маршала (Эджворта - Маршалла)
146. Задание {{ 109 }} ТЗ № 109
Если индекс переменного состава - 90 %; индекс структурных сдвигов - 120 %, то индекс постоянного состава (в %) равен..... (Результат ввести без указания единиц измерения).
Правильные варианты ответа: 75;
147. Задание {{ 110 }} ТЗ № 110
Компромиссными формами индексов, учитывающих сдвиги в структуре товарной массы в отчетном и базисном периодах являются индексы цен
£ Пааше
£ Ласпейреса
R Фишера
R Эджворта-Маршалла
148. Задание {{ 111 }} ТЗ № 111
Формулы индекса переменного состава имеют вид
£ 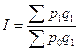
R 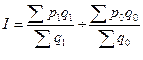
£ 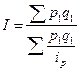
R 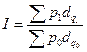
149. Задание {{ 112 }} ТЗ № 112
Общим индексом производительности труда (по трудоемкости) является
£ 
£ 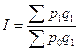
£ 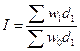
R 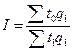
150. Задание {{ 113 }} ТЗ № 113
В теории статистики в зависимости от степени охвата единиц совокупности различают следующие индексы
£ нормальные
R сводные (общие)
£ локальные
R индивидуальные (частные)
151. Задание {{ 114 }} ТЗ № 114
В теории статистики индекс переменного состава вычисляют как произведение следующих показателей
£ цепных индексов
£ индивидуальных индексов
R индекс фиксированного состава
R индекс структурных сдвигов
152. Задание {{ 115 }} ТЗ № 115
В теории статистики устанавливается, что изменение среднего значения качественного показателя обусловлено изменением следующих факторов
£ базы сравнения
R значений показателя
£ методологии сбора данных
R структуры явления
153. Задание {{ 116 }} ТЗ № 116
По данным статистики за отчетный период потребительские цены возросли на 25 %. Индекс покупательной способности рубля может быть выражен следующими из нижепредставленных данных
R 0,8
£ 25 %
R 80 %
£ 0,25
154. Задание {{ 117 }} ТЗ № 117
В теории статистики агрегатный индекс представляет собой отношение сумм произведений двух величин
R показателя, выбранного в качестве соизмерителя (веса)
£ показателя интенсивности
R индексируемого показателя
£ показателя сравнения
155. Задание {{ 118 }} ТЗ № 118
В теории статистики для расчета индивидуальных индексов необходимы следующие данные
£ среднее значение показателя
£ вес (соизмеритель)
R значение i-го показателя в отчетном периоде
R значение i-го показателя в базисном периоде
156. Задание {{ 212 }} ТЗ № 212
Индекс покупательной способности рубля представляет собой величину,
£ равную индексу потребительских цен
£ полученную в результате вычитания индексов
R обратную индексу потребительских цен
£ которая не связана с индексом потребительских цен
157. Задание {{ 213 }} ТЗ № 213
Индексы динамики средней себестоимости единицы продукции по совокупности производственных единиц, выпускающих однородную продукцию (индекс переменного состава) - это
£ 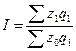
£ 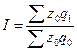
£ 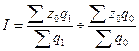
R 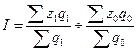
158. Задание {{ 214 }} ТЗ № 214
Общий индекс себестоимости - это
£ 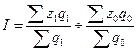
R 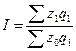
£ 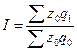
£ 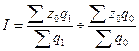
159. Задание {{ 215 }} ТЗ № 215
Общий индекс физического объема - это
£ 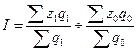
£ 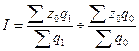
R 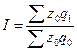
£ 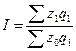
160. Задание {{ 221 }} ТЗ № 221
В теории статистики в зависимости от индексируемого показателя различают индексы
£ факторных показателей
R количественных (объемных) показателей
R качественных показателей
£ результативных показателей
161. Задание {{ 222 }} ТЗ № 222
В статистике уровня жизни населения для расчета индекса реальной заработной платы используют данные индексов
£ совокупных доходов
£ товарооборота
R потребительских цен
R номинальной заработной платы
162. Задание {{ 231 }} ТЗ № 231
В общем индексе цен индексируемой величиной будет выступать:
R цена на единицу продукции
£ структура объема произведенной продукции
£ объем произведенной продукции
£ затраты на один рубль произведенной продукции
163. Задание {{ 176 }} ТЗ № 176
Абсолютный размер экономии (перерасхода) покупателей в результате изменения цен на группу товаров определяется как разность
£ числителя и знаменателя индекса цен переменного состава
R числителя и знаменателя индекса цен
£ индекса товарооборота и индекса цен
£ числителя и знаменателя индекса стоимости товарооборота
164. Задание {{ 177 }} ТЗ № 177
Связь между индексами переменного состава (Iпер. сост.), постоянного состава (Iпост. сост.) и структурных сдвигов (Iстр. сдв.) определяется выражением
£ Iпер. сост. = Iпост. сост./Iстр. сдв.
R Iпер. сост. = Iпост. сост.*Iстр. сдв.
£ Iстр. сдв. = Iпост. сост.*Iпер. сост.
£ Iпост. сост. = Iпер. сост.*Iстр. сдв.
165. Задание {{ 178 }} ТЗ № 178
Постоянная величина, влияние которой устраняется в индексе, но она обеспечивает соизмеримость совокупности, называется
£ индексируемой величиной
£ вариантой
£ частотой
R весом
166. Задание {{ 179 }} ТЗ № 179
По данным статистики на предприятии индекс физического объема продукции в отчетном периоде по сравнению с базисным составил 120%, индекс цен фиксированного состава на продукцию предприятия составил 110%. Изменение дохода от реализации продукции может быть выражена следующими данными
R увеличился на 32%
R увеличился в 1,32 раза
£ снизился в 1,09раза
£ снизился на 9%
167. Задание {{ 180 }} ТЗ № 180
Цепные индексы получают путем сопоставления
£ предшествующего уровня с текущим
£ текущего уровня со средним
£ текущего уровня с уровнем какого-либо периода, принятого за базу сравнения
R текущего уровня с предшествующим
168. Задание {{ 234 }} ТЗ № 234
По степени охвата элементов совокупности индексы подразделяются на
£ динамические и территориальные
R индивидуальные и общие
£ постоянного и переменного состава
£ агрегатные и средние
169. Задание {{ 119 }} ТЗ № 119
Базисные индексы получают путем сопоставления
£ текущего уровня со средним
R текущего уровня с уровнем какого-либо периода, принятого за базу сравнения
£ текущего уровня с предшествующим
£ предшествующего уровня с текущим
170. Задание {{ 120 }} ТЗ № 120
Имеются данные о количестве проданных товаров. Товарооборот в базисном периоде составил 25000 руб., в отчетном периоде 30000 руб. Согласно теории статистики можно утверждать следующее
£ индекс товарооборота равен 5000 руб.
R товарооборот в текущем периоде увеличился на 20 %
R индекс товарооборота равен 1,2
£ товарооборот в отчетном периоде увеличился на 120 %
171. Задание {{ 121 }} ТЗ № 121
Объем продаж базисного периода берется в качестве весов при расчете индекса цен
£ Фишера
£ Эджворта-Маршала (Эджворта-Маршалла)
R Ласпейреса
£ Пааше
172. Задание {{ 122 }} ТЗ № 122
Относительное изменение товарооборота под влиянием изменения цен на продукцию характеризует
£ общий индекс товарооборота
£ индекс средней цены постоянного состава
£ индивидуальный индекс цен
R агрегатный индекс цен
173. Задание {{ 123 }} ТЗ № 123
В теории статистики изменение объема реализации товара А в стоимостном выражении отражает
£ средний индекс товарооборота
£ индивидуальный индекс цен
R индивидуальный индекс товарооборота
R произведение индивидуальных индексов цены и физического объема реализации
174. Задание {{ 124 }} ТЗ № 124
В теории статистики для вычисления сводного индекса физического объема товаров по формуле средней арифметической взвешенной используют следующие данные по каждому виду товаров
£ индивидуальный индекс товарооборота
R индивидуальный индекс физического объема товарооборота
£ товарооборот текущего периода
R товарооборот базисного периода
175. Задание {{ 125 }} ТЗ № 125
По формуле рассчитывается общий индекс цен
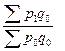
R Ласпейреса
£ Фишера
£ Эджворта-Маршалла
£ Пааше
176. Задание {{ 126 }} ТЗ № 126
Доход от реализации продукции предприятия в базисном и текущем периодах составили соответственно 100 тыс. руб. и 150 тыс руб. Физический объем продукции в базисном и текущем периодах составлял 1000 единиц. Данные статистики позволяют утверждать следующее
£ изменение дохода от реализации продукции произошло за счет изменения цен и структуры продукции
R индекс цен переменного состава равен 1,5
R изменение дохода произошло за счет изменения цен
£ индекс цен переменного состава равен 0,66
177. Задание {{ 127 }} ТЗ № 127
В теории статистики в зависимости от целей исследования сводные индексы могут выражаться в следующей форме
£ индивидуальные индексы
R агрегатные индексы
R индексы средних величин
£ переменные индексы
178. Задание {{ 247 }} ТЗ № 247
При расчете территориального индекса цен в качестве весов принимают объем проданных товаров
£ примерный
£ относительный
R суммарный
£ средний
Анализ рядов динамики
179. Задание {{ 45 }} ТЗ № 45
Средний уровень абсолютных величин интервального ряда динамики
с одинаковой продолжительностью периодов времени определяется как средняя
R арифметическая простая
£ арифметическая взвешенная
£ геометрическая
£ хронологическая
180. Задание {{ 46 }} ТЗ № 46
с целью приведения несопоставимых уровней ряда динамики к сопоставимому виду применяется прием
£ укрупнения интервалов
£ аналитического выравнивания
R приведения рядов динамики к одному основанию
£ скользящей средней
181. Задание {{ 47 }} ТЗ № 47
При сопоставлении показателей каждого последующего уровня с предыдущим, показатели динамики определяются методом
£ базисным
£ интервальным
£ графическим
R цепным
182. Задание {{ 48 }} ТЗ № 48
Отношением абсолютного прироста уровня ряда за интервал времени к темпу прироста за тот же промежуток времени рассчитывается показатель
£ относительное ускорение
R абсолютное значение 1% прироста
£ абсолютный прирост
£ темп роста
183. Задание {{ 49 }} ТЗ № 49
В теории статистики ряды динамики в зависимости от показателей времени разделяются на
R моментные
£ дискретные
R интервальные
£ непрерывные
184. Задание {{ 50 }} ТЗ № 50
В статистической практике абсолютный прирост уровней ряда динамики можно вычислить по следующим данным
R цепные абсолютные приросты
£ базисные темпы роста
R начальное и конечное значения уровней ряда
£ цепные темпы прироста
185. Задание {{ 51 }} ТЗ № 51
Имеется ряд, характеризующий среднегодовую численность населения за пять лет. Согласно теории статистики можно утверждать, что это ряд
£ с неравноотстоящими уровнями
R интервальный
£ моментный
R с равноотстоящими уровнями
186. Задание {{ 52 }} ТЗ № 52
По данным статистики среднегодовая численность занятых в экономике города за последние три года соответственно равна (тыс. чел.) 66,8; 67,2; 67,7. Расчет среднегодового абсолютного прироста позволяет утверждать
R Численность занятых увеличивалась в среднем на 0,45 тыс. чел. в год
£ численность занятых увеличилась на 0,45 тыс. человек за период
£ среднегодовой прирост равен 300 человек
R среднегодовой прирост равен 450 человек
187. Задание {{ 53 }} ТЗ № 53
Согласно теории статистики при изучении основной тенденции в рядах динамики для вычисления отсутствующих уровней внутри и за пределами ряда решают следующие задачи
R интерполяции
R экстраполяции
£ вычисления индексов сезонности
£ построения доверительных интервалов
188. Задание {{ 54 }} ТЗ № 54
Имеются статистические данные, характеризующие цепные коэффициенты роста, равные соответственно: 1,15; 1,20; 1,25; 1,15. В этом случае можно утверждать, что средний коэффициент роста вычисляется по формуле средней....... и его величина составит
R 1,187
£ арифметической простой
£ 18,7 %
R геометрической
189. Задание {{ 55 }} ТЗ № 55
В статистической практике на основе известных цепных темпов роста прибыли организации, равных соответственно 115% и 120%, используя соотношение статистических показателей, можно получить следующие базисные темпы роста и прироста
£ 135 %
R 138 %
R 38 %
£ 35 %
190. Задание {{ 56 }} ТЗ № 56
Моментным рядом динамики является
R сумма банковских вкладов населения на конец каждого года
£ средняя заработная плата рабочих и служащих по месяцам года
R остаток материальных средств по состоянию на определенную дату каждого месяца
£ производительность труда на предприятии за каждый месяц года
191. Задание {{ 57 }} ТЗ № 57
При расчете среднего коэффициента роста с помощью средней геометрической подкоренное значение представляет собой..... При этом показатель степени равен....
R произведение цепных коэффициентов роста
£ сумму цепных коэффициентов роста
£ числу уровней ряда динамики
R числу цепных коэффициентов роста
192. Задание {{ 58 }} ТЗ № 58
Показателем, характеризующим тенденцию динамики, является
£ дисперсия
£ коэффициент вариации
R темп прироста
£ средняя арифметическая
193. Задание {{ 59 }} ТЗ № 59
Деление рядов динамики на моментные и интервальные производится по
£ расстоянию между уровнями ряда динамики
R времени
£ способу выражения уровней ряда динамики
£ величине уровней ряда динамики
194. Задание {{ 60 }} ТЗ № 60
Ряд динамики характеризует
£ определенное значение варьирующего признака в совокупности
£ структуру совокупности по какому-либо признаку
R изменение значений признака во времени
£ значение признака на определенную дату или за определенный период времени
195. Задание {{ 61 }} ТЗ № 61
Ряд динамики, характеризующий экспорт страны по каждому году за последние 5 лет, относится к рядам динамики
£ моментным
£ произвольным
£ производным
R интервальным
196. Задание {{ 62 }} ТЗ № 62
В статистической практике базисный темп роста прибыли организации за 5 лет составил 116%. В этом случае средние темпы роста и прироста составят
£ 7 %
R 104 %
£ 107 %
R 4 %
197. Задание {{ 64 }} ТЗ № 64
Согласно теории статистики связь базисных и цепных темпов роста характеризует следующие утверждения
£ базисный темп роста равен сумме цепных
R цепной темп роста равен частному от деления смежных базисных
R базисный темп роста равен произведению цепных
£ цепной темп роста равен произведению базисных
198. Задание {{ 65 }} ТЗ № 65
В теории статистики при изучении сезонных колебаний рядов динамики используют
£ график тренда
R индексы сезонности
£ индивидуальные индексы
R график сезонной волны
199. Задание {{ 66 }} ТЗ № 66
В практике статистики индекс сезонности имеет существенное значение для анализа спроса на следующие товары и услуги
R меховая одежда
£ ремонт бытовой техники
R пассажироперевозки
R продукты питания
200. Задание {{ 67 }} ТЗ № 67
В теории статистики относительные показатели изменения уровня ряда могут выражаться в следующей форме
£ абсолютный прирост
R темп роста
R коэффициент роста
£ коэффициент вариации
201. Задание {{ 75 }} ТЗ № 75
При сопоставлении каждого последующего уровня с одним и тем же, взятым за базу для сравнения, показатели динамики определяются методом
R базисным
£ моментным
£ цепным
£ интервальным
202. Задание {{ 226 }} ТЗ № 226
Имеются данные о средних остатках оборотных средств.
Дата 20.05 20.06 20.07 20.08 20.09
Средние
остатки 10 20 30 10 40
Определить среднюю величину остатков
R 21,25
£ 3,45
£ 22,0
£ 20,0
203. Задание {{ 230 }} ТЗ № 230
В статистической практике базисный темп роста прибыли организации за 5 лет составил 116%. В этом случае средние темпы роста и прироста составят
R 104 %
R 4 %
£ 7 %
£ 107 %
204. Задание {{ 233 }} ТЗ № 233
В течение трех лет среднегодовая численность занятых в экономике региона соответственно равна (тыс. чел.): 66,8; 64,2; 62,8. Расчет позволяет утверждать
£ численность занятых уменьшилась на 2 тыс. человек за период
R численность занятых уменьшалась на 2 тыс. человек в год
£ прирост равен 2 тыс. человек
R абсолютный прирост за период равен - 4 тыс. человек
205. Задание {{ 181 }} ТЗ № 181
Если численность населения на 1 января текущего года 12 тыс. чел., на первое апреля текущего года 11 тыс. чел., на 1 июля текущего года 13 тыс. человек, на первое сентября текущего года 12,5 тыс. человек, на первое января следующего года 12 тыс. чел., то средняя численность населения муниципального образования равна.... (Результат ввести в виде числа без указания единиц измерения с точностью до 0,1)
Правильные варианты ответа: 12,1;
206. Задание {{ 182 }} ТЗ № 182
Согласно теории статистики понятие "темп роста" характеризует следующие утверждения
£ может принимать любые значения
R показывает, во сколько раз отчетный уровень отличается от базисного
£ показывает, на сколько единиц отчетный уровень отличается от базисного
R может принимать только положительные значения
207. Задание {{ 183 }} ТЗ № 183
Имеются ряды, уровни которых характеризуют величину прибыли организации за четыре квартала года. Согласно теории статистики можно утверждать, что это ряд
R интервальный
£ моментный
R динамический
£ вариационный
208. Задание {{ 184 }} ТЗ № 184
В статистической практике для расчета средних значений уровней рядов динамики используют
R среднюю арифметическую
R среднюю хронологическую
£ структурные средние
£ среднюю гармоническую
209. Задание {{ 185 }} ТЗ № 185
Имеется ряд динамики, уровни которого соответственно равны 60, 50, 45 единиц. Согласно теории статистики на основе приведенных данных можно утверждать следующее
R абсолютный прирост уменьшается по абсолютной величине
£ темп прироста снижается
R темп роста увеличивается
£ темп роста снижается
210. Задание {{ 186 }} ТЗ № 186
По данным статистики прибыль предприятия увеличилась за первый год на 30%, за второй год - на 40%. Увеличение объема прибыли за два года может быть выражено следующими из нижеперечисленных данных
R в 1,82 раза
£ в 1,35 раза
R на 82%
£ на 35%
211. Задание {{ 187 }} ТЗ № 187
По данным статистики среднегодовая численность занятых в экономике города за последние три года соответственно равны (тыс. чел.) 66,8; 67,2; 67,7. Расчет среднегодового абсолютного прироста позволяет утверждать
R среднегодовой прирост равен 450 человек
£ среднегодовой прирост равен 300 человек
R численность занятых увеличилась в среднем на 0,45 тыс. чел. в год
£ численность занятых увеличилась на 0,45 тыс. чел. за период
212. Задание {{ 238 }} ТЗ № 238
В теории статистики базисный абсолютный прирост может быть вычислен как
£ среднее арифметическое начального и конечного уровней ряда
R сумма цепных абсолютных приростов
£ частное от деления конечного и начального уровней ряда
R разность i-ого и начального уровней ряда