МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПРИБОРОСТРОЕНИЯ И ИНФОРМАТИКИ
Кафедра _ИС–1–Информационно–управляющие системы___________________________________________
(шифр и наименование кафедры)
УТВЕРЖДАЮ
Заведующий кафедрой
_________ (В.Д. Ивченко)
«___»_________200__г.
Для студентов 4_ курса факультета ИС
специальности 220201–управление и информатика в технических системах
Пакет прикладных программ
«STATUS»
по 3121– Случайные процессы в системах управления
Обсужден на заседании кафедры
(предметно-методической секции)
«__»___________200__г.
Протокол № __
МГУПИ – 200__г.
АННОТАЦИЯ
В процессе создания управляемых систем большую роль играет моделирование этих систем на ЭВМ (так называемый «машинный эксперимент»). В то же самое время при решении задач моделирования систем на ЭВМ к числу основных вопросов относятся как воспроизведение стохастических сигналов, действующих на входах этих систем, так и последующая оценка качества моделирования случайных процессов (СП). В свою очередь, успешное решение этих задач способствует качественному решению и вопросов моделирования управляемых систем в целом.
Данный пакет прикладных программ (ППП) разработан для решения широкого круга задач, связанных с моделированием и статистическим анализом скалярных и векторных СП. Пакет написан на алгоритмическом языке ФОРТРАН - 4 и ориентирован на ЭВМ типа IBM PC. Он предназначается для ознакомления студентов с методами моделирования стохастических воздействий и используется студентами 4–ого курса для выполнения лабораторных работ по дисциплине «Случайные процессы в системах управления». ППП может быть использован также студентами старших курсов, занимающимися научной работой, и в процессе выполнения дипломного проектирования.
СОДЕРЖАНИЕ
1. Головная программа 5
2. Управляющие подпрограммы 9
2.1. Автономная подпрограмма GENER1 10
3. Подпрограммы генерирования реализации СП. 14
3.1. Автономная подпрограмма ISTOK1 15
3.2. Автономная подпрограмма ISTOKM. 18
3.3. Автономная подпрограмма-функция GAUSS 21
3.4. Автономная подпрограмма-функция RELEY 22
3.5. Автономная подпрограмма-функция EXPON 23
3.6. Автономная подпрограмма KANON1 24
4. Вспомогательные, подпрограммы 29
4.1. Автономная подпрограмма RAZM1 30
4.2. Автономная подпрограмма RAZMM 31
4.3. Автономная подпрограмма FORM 32
5. Подпрограммы центрирования реализации СП 34
5.1. Автономная подпрограмма CENTR1 35
5.2. Автономная подпрограмма CENTRM 36
6. Подпрограммы расчета статистических корреляционных моментов СП 37
6.1. Автономная подпрограмма K0RM1 38
6.2. Автономная подпрограмма КОRММ 39
7. Подпрограмма расчета статистических нормированных
корреляционных функций СП 40
7.1. Автономная подпрограмма КОRF1 41
7.2. Автономная подпрограмма KORF2 42
7.3. Автономная подпрограмма КОRFМ 44
7.4. Автономная подпрограмма KORFA1 45
7.5. Автономная подпрограмма-функция FUNC1 47
8. Подпрограммы расчета статистических нормированных
функций спектральной плотности. 49
8.1. Автономная подпрограмма FORMF1 50
8.2. Автономная подпрограмма SPID1 51
8.3. Автономная подпрограмма SPID2. 52
8.4. Автономная подпрограмма SPIDM 54
8.5. Автономная подпрограмма SPIN1 56
8.Подпрограммы расчета статистических функций
плотности вероятности СП 58
9.1. Автономная подпрограмма FORMX1 59
9.2. Автономная подпрограмма FORMXM. 60
9.3. Автономная подпрограмма GIST1. 62
9.4. Автономная подпрограмма GIST2 63
9.5. Автономная подпрограмма GISTM 65
10. Подпрограммы расчета заданных /теоретических/ статистических
характеристик СП 67
10.1. Автономная подпрограмма TEST1 68
11. Подпрограммы анализа точности воспроизведения
статистических характеристик СП. 72
11.1. Автономная подпрограмма ANALI 73
12. Запуск ППП 76
Список литературы
1. ГОЛОВНАЯ ПРОГРАММА
Данная программа предназначается для ввода и вывода исходных данных управляющих подпрограмм, а также для обращения к последним.
Первым элементом ввода программ является признак JREG /идентификатор JREGIM/, определяющий режим работы программы, который вводится оператором READ в формате 15.
Ввод исходных данных управляющей подпрограммы GENER1 и обращение к этой подпрограмме осуществляется только при выполнении условия:
JREG = 1
Ввод исходных данных управляющей подпрограммы GENER1 осуществляется с помощью пяти операторов READ.
Первая группа исходных данных подпрограммы GENER1 вводится в формате 515 и включает в себя:
JPLOV - признак Jf вида функции плотности вероятности f(X) СП Х(Т); Jf 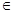 [1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
[1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
JKORF - признак Jr вида нормированной корреляционной функции 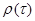 СП Х(Т); Jr
СП Х(Т); Jr 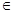 [1, 5 ] /некоррелированному СП соответствует Jr = 1, коррелированному СП - Jr > 1, не дифференцируемому СП - Jr = 2 или Jr = 4, дифференцируемому СП - Jr = 3 или Jr = 5, СП, обладающему монотонной корреляционной функцией, - Jr = 2 или Jr = 3, СП, обладающему немонотонной корреляционной санкцией, - Jr = 4 или Jr =5/;
[1, 5 ] /некоррелированному СП соответствует Jr = 1, коррелированному СП - Jr > 1, не дифференцируемому СП - Jr = 2 или Jr = 4, дифференцируемому СП - Jr = 3 или Jr = 5, СП, обладающему монотонной корреляционной функцией, - Jr = 2 или Jr = 3, СП, обладающему немонотонной корреляционной санкцией, - Jr = 4 или Jr =5/;
JSPEK - признак JS способа расчета статистической функции спектральной плотности 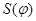 СП Х(Т); JS
СП Х(Т); JS 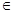 [0, 1] /расчету, основанному на использовании формул численного интегрирования, соответствует JS = 0, а расчету, основанному на использовании квадратурных формул интегрирования и аппроксимационных формул для статистической корреляционной функции, JS = I/;
[0, 1] /расчету, основанному на использовании формул численного интегрирования, соответствует JS = 0, а расчету, основанному на использовании квадратурных формул интегрирования и аппроксимационных формул для статистической корреляционной функции, JS = I/;
JKORFA - признак Jr,a необходимости построения аппроксимационной зависимости для статистической корреляционной функции СП Х(Т), а также корректировки на ее основе этой функции; Jr,a 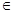 [1, 5] /указанные операции проводятся только в случае Jr,a >1, а вид аппроксимационной зависимости при этом определяется величиной данного признака по тому же самому принципу, по которому вид заданной корреляционной функции определяется величиной признака Jr,a /;
[1, 5] /указанные операции проводятся только в случае Jr,a >1, а вид аппроксимационной зависимости при этом определяется величиной данного признака по тому же самому принципу, по которому вид заданной корреляционной функции определяется величиной признака Jr,a /;
JSTAT - признак JSTAT необходимости проведения статистической обработки сгенерированной дискретизированной реализации СП Х(Т) в целом; JSTAT 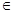 [0,1];
[0,1];
Вторая группа исходных данных подпрограммы GENER1 вводится в формате 415 и включает в себя:
JRPLOV - признак JR,f необходимости проведения статистической обработки реализации СП Х(Т) в части расчета функции плотности вероятности; JR,f 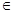 [0,1];
[0,1];
JRKORF - признак JR,r необходимости проведения статистической обработки реализации СП Х(Т) в части расчета корреляционной функции; JR,r 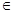 [0,1];
[0,1];
JRSPEK - признак JR,S - необходимости проведения статистической обработки реализации СП Х(Т) в части расчета функции спектральной плотности; JR,S 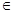 [0,1];
[0,1];
N- число узлов дискретизации реализации СП Х(Т).
Третья группа исходных данных подпрограммы (GENER1 вводится в формате 415 и включает в себя:
NPLOV - число узлов дискретизации функции f(X);
NKORF - число узлов дискретизации функции 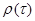 ;
;
NSPEK - число узлов дискретизации функции 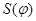 ;
;
NPP - число предварительных прокруток алгоритма генерирования реализации СП Х(Т) на режиме "холостого хода" /к использованию рекомендуется значение этого параметра, составляющее примерно 10 % от величины параметра N/.
Четвертая группа исходных данных подпрограммы GENER1 вводится в формате 4F10.2 и включает в себя:
PI, P2 - параметры p1 и р2 функции f(Х) генерируемого СП Х(Т);
Z0 - начальное значение последовательности псевдослучайных чисел /любое целое положительное нечетное число, не превышающее 67108864/;
DTAU - шаг 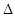 дискретизации реализации СП Х(Т), с.
дискретизации реализации СП Х(Т), с.
Пятая группа исходных данных подпрограммы GENER1 вводится в формате 3F10.2, 2F10.2, ЗF10.2 и включает в себя:
MАК (3) - массив параметров нормированной корреляционной функции генерируемого СП Х(Т) /MAK (I) и МАК (2) – подэкспоненциальные множители 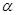 и
и 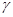 ; МАK (З) - характерная частота процесса j0,Гц/,
; МАK (З) - характерная частота процесса j0,Гц/,
MAFI (2) - массив параметров, определяющих границы шкалы аргумента функции 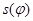 / MAFI (1)- jNACH, MAFI (2) - jK0N; jK0N > jNACH/, Гц;
/ MAFI (1)- jNACH, MAFI (2) - jK0N; jK0N > jNACH/, Гц;
МАКАР (3) - массив начальных приближений параметров 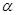 ,
, 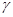 и j0 для оптимальной аппроксимации статистической корреляционной функции.
и j0 для оптимальной аппроксимации статистической корреляционной функции.
Все указанные выше операции, выполнение которых зависит от значений признаков, определенных на области [0,1], производится только при ненулевых значениях этих признаков.
Функции плотности вероятности СП Х(Т) для различных законов распределения из числа рассматриваемых в программе записываются в форме:
при Jf = l
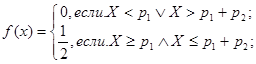
при Jf = 2
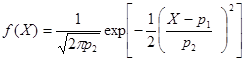 ;
;
при Jf = 3
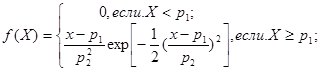
при Jf = 4

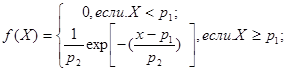
Корреляционные функции СП Х(Т) из числа допускаемых к использованию в программе записываются в форме:
при Jr = 1
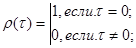
при Jr = 2
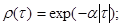
при Jr = 3
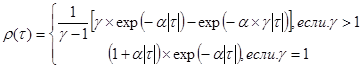
при Jr = 4
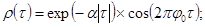
при Jr = 5
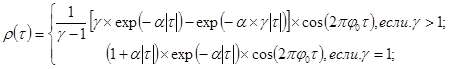
2. УПРАВЛЯЮЩИЕ ПОДПРОГРАММЫ
Подпрограммы, включенные в данный раздел пакета, предназначаются для выполнения следующих операций:
генерирования дискретизированной реализации одномерного /скалярного/ СП, который подчиняется одному из законов распределения из числа заданных и обладает одной из корреляционных функций из числа заданных /для коррелированных СП допускается использование только нормального закона распределения/;
статистической обработки этой реализации.
2.1. АВТОНОМНАЯ ПОДПРОГРАММА GENER1
Данная подпрограмма написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения комплекса операций, связанных с генерированием дискретизированной реализации стационарного одномерного /скалярного/ СП, подчиняющегося заданному закону распределения и обладающего корреляционной функцией заданного типа.
В подпрограмме содержится обращение к автономным подпрограммам ISTOK1, KANON1, CENTR1, К0RM1, RAZM1, KOPF1, FOPMF1, КОRFA1, SPID1, SPIN1, FORMX1, GIST1, TEST1 и ANALI.
Обращение к подпрограмме имеет вид:
CALL GENER1 (JPLOV, JKORF, JSPEK, JKORFA, JSTAT, JRPLOV, JRKOPF, JRSPEK, N, NPLOV, NKORF, NSPEK, NPP, P1, P2, Z0, MAK, MAF1,MAKAP)
Здесь:
JPLOV - признак Jf вида функции плотности вероятности f(X) СП Х(Т); Jf 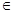 [1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
[1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
JKORF - признак Jr вида нормированной корреляционной функции 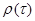 СП Х(Т); Jr
СП Х(Т); Jr 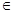 [1, 5 ] /некоррелированному СП соответствует Jr = 1, коррелированному СП - Jr > 1, не дифференцируемому СП - Jr = 2 или Jr = 4, дифференцируемому СП - Jr = 3 или Jr = 5, СП, обладающему монотонной корреляционной функцией, - Jr = 2 или Jr = 3, СП, обладающему немонотонной корреляционной санкцией, - Jr = 4 или Jr =5/;
[1, 5 ] /некоррелированному СП соответствует Jr = 1, коррелированному СП - Jr > 1, не дифференцируемому СП - Jr = 2 или Jr = 4, дифференцируемому СП - Jr = 3 или Jr = 5, СП, обладающему монотонной корреляционной функцией, - Jr = 2 или Jr = 3, СП, обладающему немонотонной корреляционной санкцией, - Jr = 4 или Jr =5/;
JSPEK - признак JS способа расчета статистической функции спектральной плотности 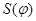 СП Х(Т); JS
СП Х(Т); JS 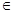 [0, 1] /расчету, основанному на использовании формул численного интегрирования, соответствует JS = 0, а расчету, основанному на использовании квадратурных формул интегрирования и аппроксимационных формул для статистической корреляционной функции, JS = I/;
[0, 1] /расчету, основанному на использовании формул численного интегрирования, соответствует JS = 0, а расчету, основанному на использовании квадратурных формул интегрирования и аппроксимационных формул для статистической корреляционной функции, JS = I/;
JKORFA - признак Jr,a необходимости построения аппроксимационной зависимости для статистической корреляционной функции СП Х(Т), а также корректировки на ее основе этой функции; Jr,a 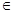 [1, 5] /указанные операции проводятся только в случае Jr,a >1, а вид аппроксимационной зависимости при этом определяется величиной данного признака по тому же самому принципу, по которому вид заданной корреляционной функции определяется величиной признака Jr,a /;
[1, 5] /указанные операции проводятся только в случае Jr,a >1, а вид аппроксимационной зависимости при этом определяется величиной данного признака по тому же самому принципу, по которому вид заданной корреляционной функции определяется величиной признака Jr,a /;
JSTAT - признак JSTAT необходимости проведения статистической обработки сгенерированной дискретизированной реализации СП Х(Т) в целом; JSTAT 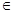 [0,1];
[0,1];
Вторая группа исходных данных подпрограммы GENER1 вводится в формате 415 и включает в себя:
JRPLOV - признак JR,f необходимости проведения статистической обработки реализации СП Х(Т) в части расчета функции плотности вероятности; JR,f 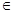 [0,1];
[0,1];
JRKORF - признак JR,r необходимости проведения статистической обработки реализации СП Х(Т) в части расчета корреляционной функции; JR,r 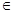 [0,1];
[0,1];
JRSPEK - признак JR,S - необходимости проведения статистической обработки реализации СП Х(Т) в части расчета функции спектральной плотности; JR,S 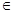 [0,1];
[0,1];
N- число узлов дискретизации реализации СП Х(Т).
NPLOV - число узлов дискретизации функции f(X);
NKORF - число узлов дискретизации функции 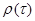 ;
;
NSPEK - число узлов дискретизации функции 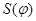 ;
;
NPP - число предварительных прокруток алгоритма генерирования реализации СП Х(Т) на режиме "холостого хода" /к использованию рекомендуется значение
этого параметра, составляющее примерно 10 % от величины параметра N/.
PI, P2 - параметры p1 и р2 функции f(Х) генерируемого СП Х(Т);
Z0 - начальное значение последовательности псевдослучайных чисел /любое целое положительное нечетное число, не превышающее 67108864/;
DTAU - шаг 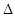 дискретизации реализации СП Х(Т), с.
дискретизации реализации СП Х(Т), с.
X(N)- массив дискретизированной с постоянным шагом 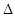 по временной координате Т реализации СП Х(Т);
по временной координате Т реализации СП Х(Т);
MАК (3) - массив параметров нормированной корреляционной функции генерируемого СП Х(Т) /MAK (I) и МАК (2) – подэкспоненциальные множители 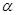 и
и 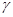 ; МАK (З) - характерная частота процесса j0,Гц/,
; МАK (З) - характерная частота процесса j0,Гц/,
MAFI (2) - массив параметров, определяющих границы шкалы аргумента функции 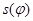 / MAFI (1)- jNACH, MAFI (2) - jK0N; jK0N > jNACH/, Гц;
/ MAFI (1)- jNACH, MAFI (2) - jK0N; jK0N > jNACH/, Гц;
МАКАР (3) - массив начальных приближений параметров 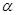 ,
, 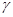 и j0 для оптимальной аппроксимации статистической корреляционной функции.
и j0 для оптимальной аппроксимации статистической корреляционной функции.
Все указанные выше операции, выполнение которых зависит от значений признаков, определенных на области [0,1], производится только при ненулевых значениях этих признаков.
Функции плотности вероятности СП Х(Т) для различных законов распределения из числа рассматриваемых в программе записываются в форме:
при Jf = l
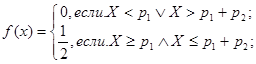
при Jf = 2
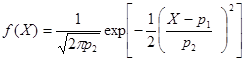 ;
;
при Jf = 3
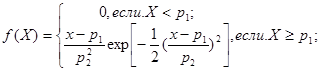
при Jf = 4

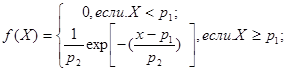
Корреляционные функции СП Х(Т) из числа допускаемых к использованию в программе записываются в форме:
при Jr = 1
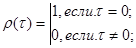
при Jr = 2
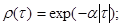
при Jr = 3
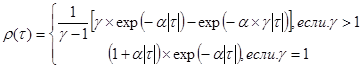
при Jr = 4
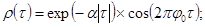
при Jr = 5
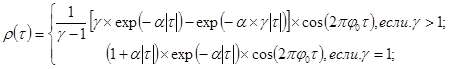
В процессе функционирования данной подпрограммы в зависимости от значений управляющих признаков производится опрос различных тематических модулей, предназначенных для выполнения отдельных операций, связанных с генерированием и статистической обработкой реализации СП Х(Т). Расчетные соотношения, используемые при выполнении отдельных видов статистических расчетов, приводятся в описаниях соответствующих автономных подпрограмм.
3. ПОДПРОГРАММЫГЕНЕРИРОВАНИЯ РЕАЛИЗАЦИИ СП
Подпрограммы, включенные в данный раздел пакета, предназначается для выполнения следующих операций:
генерирования реализации одномерного /скалярного/ некоррелированного СП, подчиняющегося одному из законов распределения из числа заданных /подпрограмма ISTOK1/;
генерирования реализации многомерного /векторного/ некоррелированного СП, подчиняющегося одному из законов распределения из числа заданных /подпрограмма ISTOKМ/;
нахождения значения СП, подчиняющегося нормальному закону распределения, которое соответствует заданному значению функции распределения этого процесса /подпрограмма-функция GAUSS/;
нахождения значения СП, подчиняющегося закону распределения Рэлея, которое соответствует заданному значению функции распределения этого процесса /подпрограмма-функция RELEY;
нахождения значения СП, подчиняющегося экспоненциальному закону распределения, которое соответствует заданному значению функции распределения этого процесса /подпрограмма-функция EXPO /;
генерирования реализации одномерного /скалярного/ СП, обладающего одной из корреляционных функций из числа заданных /подпрограмма KANON1/.
3.1. АВТОНОМНАЯ ПОДПРОГРАММА ISTOK1
Данная подпрограмма написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции генерирования дискретизированной реализации стационарного некоррелированного одномерного /скалярного/ СП, подчиняющегося заданному закону распределения из числа предусмотренных в подпрограмме.
В подпрограмме содержится обращение к автономным подпрограммам-функциям GAUSS, RELEY, EXPON.
Обращение к подпрограмме имеет вид:
CALL ISTOK1 (X,N, JPLOV, P1, P2, NPP,Z0).
Здесь:
N- число узлов в массиве Х;
X(N)- массив дискретизированной с постоянным шагом по временной координате Т реализации СП Х(Т);
JPLOV - признак Jf вида функции плотности вероятности f(X) СП Х(Т); Jf 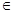 [1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
[1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
PI, P2 - параметры p1 и р2 функции f(Х);
NPP - число Npp предварительных прокруток алгоритма генерирования реализации СП Х(Т) на режиме "холостого хода" /к использованию рекомендуется значение этого параметра, составляющее примерно 10 % от величины параметра N/;
Z0 - начальное значение последовательности псевдослучайных чисел /любое целое положительное нечетное число, не превышающее 67108864/, Z0.
Функции плотности вероятности СП Х(Т) для различных законов распределения из числа рассматриваемых в программе записываются в форме:
при Jf = l
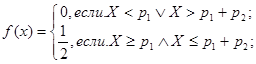
при Jf = 2
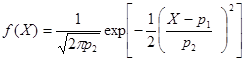 ;
;
при Jf = 3
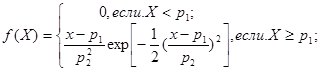
при Jf = 4

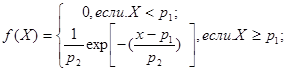
Операция вычисления значении дискретизированного СП Х(Т) в подпрограмме производится по следующим рекуррентным соотношениям, реализующим метод обратной функции распределения:
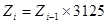 ;
; 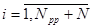 ;
;
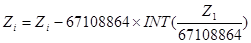 ;
; 
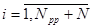 ;
;
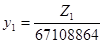 ;
; 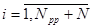 ;
;
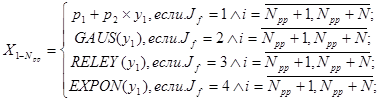
Под yi здесь понимается 1-ый элемент последовательности псевдослучайных чисел, распределенных по равномерному закону в интервале (0, 1), под выражением INT(А)- целая часть вещественного числа А, а под выражениями GAUSS(А), RELEY(A) и EXPON(А) - обратные -функции распределения соответственно нормального, рэлеевского и экспоненциального законов распределения, определяющие величину СП Х(Т), для которой функция распределения равна А.
3.2. АВТОНОМНАЯ ПОДПРОГРАММА ISTOK1
Данная подпрограмма написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции генерирования дискретизированной реализации стационарного некоррелированного многомерного /векторного/ СП, подчиняющегося заданному закону распределения из числа предусмотренных в подпрограмме.
В подпрограмме содержится обращение к автономным подпрограммам-функциям GAUSS, RELEY, EXPON.
Обращение к подпрограмме имеет вид:
CALL ISTOKM(X, N, M, JPLOV P1, P2, NPP, Z0).
Здесь:
X(N, M)- массив дискретизированной с постоянным шагом по временной координате Т реализации СП Х(Т);
N- число узлов в массиве Х, относящихся к одной составляющей векторного массива СП;
М- число составляющих векторного СП;
JPLOV - признак Jf вида функции плотности вероятности f(X) СП Х(Т); Jf 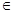 [1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
[1,4] /равномерному закону распределения соответствует Jf = 1, нормальному закону распределения - Jf = 2, закону распределения Рэлея - Jf = 3, экспоненциальному закону распределения - Jf = 4/;
PI, P2 - параметры p1 и р2 функции f(Х);
NPP - число Npp предварительных прокруток алгоритма генерирования реализации СП Х(Т) на режиме "холостого хода" /к использованию рекомендуется значение этого параметра, составляющее примерно 10 % от величины параметра N/;
Z0 - начальное значение последовательности псевдослучайных чисел /любое целое положительное нечетное число, не превышающее 67108864/, Z0.
Функции плотности вероятности СП Х(Т) для различных законов распределения из числа рассматриваемых в программе записываются в форме:
при Jf = l
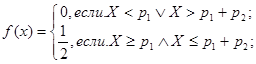
при Jf = 2
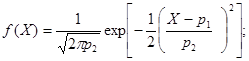
при Jf = 3
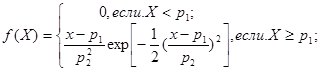
при Jf = 4

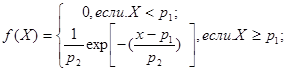

Операция вычисления значении дискретизированного СП Х(Т) в подпрограмме производится по следующим рекуррентным соотношениям, реализующим метод обратной функции распределения:
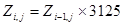 ;
; 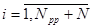 ;
; 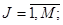
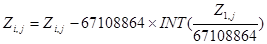 ;
; 
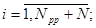
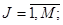
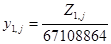 ;
; 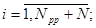
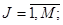
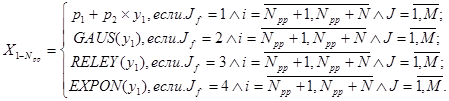
Под yi,j здесь понимается 1-ый элемент j-ой последовательности псевдослучайных чисел, распределенных по равномерному закону в интервале (0, 1), под выражением INT(А)- целая часть вещественного числа А, а под выражениями GAUSS(А), RELEY(A) и EXPON(А) - обратные -функции распределения соответственно нормального, рэлеевского и экспоненциального законов распределения, определяющие величину СП Х(Т), для которой функция распределения равна А.
3.3. АВТОНОМНАЯ ПОДПРОГРАММА - ФУНКЦИЯ GAUSS
Данная подпрограмма-функция написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции вычисления значения СП, подчиняющегося нормальному закону распределения, которое соответствует заданному значению функции распределения этого процесса.
Обращение к подпрограмме-функции имеет вид:
Х = GAUSS(Y, P1, P2).
Здесь:
Х - искомое значение СП;
Y - заданное значение функции распределения СП;
PI, P2 - параметры р1- и p2 функции плотности вероятности СП, подчиняющегося нормальному закону распределения, при записи ее в форме:
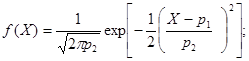
Операция вычисления значения нормального СП, соответствующего заданному значению функции распределения этого процесса, проводится в подпрограмме-функции по следующим расчетным соотношениям, аппроксимирующим обратную функцию распределения:
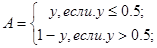
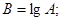
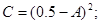
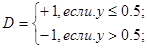
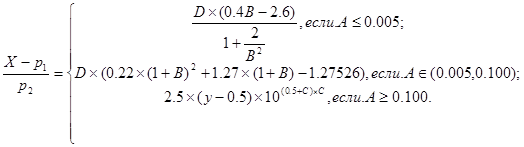
3.4. АВТОНОМНАЯ ПОДПРОГРАММА - ФУНКЦЯ RELEY
Данная подпрограмма-функция написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции вычисления значения СП, подчиняющегося рэлеевскому закону распределения, которое соответствует заданному значению функции распределения этого процесса,
Обращение к подпрограмме-функции имеет вид:
Х = RELEY (Y, PI. P2),
Здесь:
Х - искомое значение СП;
Y - заданное значение функции распределения СП;
PI, P2 - параметры р1- и p2 функции плотности вероятности СП, подчиняющегося нормальному закону распределения, при записи ее в форме:
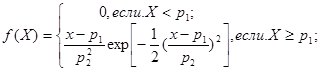
Операция вычисления значения нормального СП, соответствующего заданному значению функции распределения этого процесса, проводится в подпрограмме-функции по следующим расчетным соотношениям, аппроксимирующим обратную функцию распределения:
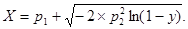
3.5. АВТОНОМНАЯ ПОДПРОГРАММА-ФУНКЦИЯ EXPON
Данная подпрограмма-функция: написана на алгоритмическом языке ФОРТРАЕ-4 и предназначается для проведения операции вычисления значения СП, подчиняющегося экспоненциальному закону распределения, которое соответствует заданному значению функции распределения этого процесса.
Обращение к подпрограмме-функции имеет вид:
Х = EXPON(Y, PI, P2).
Здесь:
Х - искомое значение СП;
Y - заданное значение функции распределения СП;
PI, P2 - параметры р1- и p2 функции плотности вероятности СП, подчиняющегося нормальному закону распределения, при записи ее в форме:
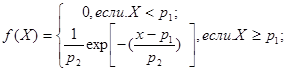

Операция вычисления значении дискретизированного СП Х(Т) в подпрограмме производится по следующим рекуррентным соотношениям, реализующим метод обратной функции распределения:
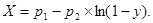
3.6. АВТОНОМНАЯ ПОДПРОГРАММА KANON1
Данная подпрограмма написана на алгоритмическом языке ФОРТРАН-4 и предназначается для проведения операции генерирования дискретизированной реализации стационарного коррелированного одномерного /скалярного/ СП, подчиняющегося заданному закону распределения и обладающего корреляционной функцией заданного типа.
Обращение к подпрограмме имеет вид:
CALL KANON1 (X, N, Е, D, R0, NR0, А, В, С, F).
Здесь:
X(N) - на входе в подпрограмму - массив случайных величин Нк, некоррелированных между собой, подчиняющихся заданному закону распределения и характеризующихся нулевым математическим ожиданием и единичной дисперсией, а на выходе из подпрограммы - массив сформированной дискретизированной с постоянным шагом по временной координате Т реализации СП Х(Т), обладающей статистическими характеристиками, близкими к заданным;
N- число узлов в массиве X;
Е, D - заданные значения математического ожидания и дисперсии генерируемого СП;
R0 (NRO) - массив заданных значений нормированной корреляционной функции 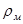 генерируемого СП, соответствующих равноотстоящим друг от друга /с шагом дискретизации реализации СП/ значениям ее аргумента
генерируемого СП, соответствующих равноотстоящим друг от друга /с шагом дискретизации реализации СП/ значениям ее аргумента 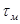 ;
;
NR0 - число узлов 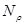 массиве R0;
массиве R0;
A (NRO, NRO) - рабочая матрица;
В, С, F (NRO) - рабочие массивы.
Операция вычисления значений дискретизированного СП Х(Т), соответствующего заданному закону распределения и обладающего корреляционной функцией заданного типа, производится в подпрограмме в рамках метода канонических разложений.
Согласно указанному методу центрированная случайная функция 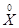 разлагается в ряд вида:
разлагается в ряд вида:
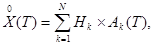 (1)
(1)
где под 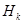 понимаются случайные величины, некоррелированные между собой и характеризующиеся нулевым математическим ожиданием, а под
понимаются случайные величины, некоррелированные между собой и характеризующиеся нулевым математическим ожиданием, а под 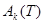 - детерминированные координатные функции времени.
- детерминированные координатные функции времени.
Простейший алгоритм реализации, метода канонических разложений для дискретной реализации функции 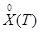 , определенной в равноотстоящих узлах, формируется следующим образом:
, определенной в равноотстоящих узлах, формируется следующим образом:
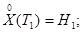 (2)
(2)
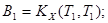 (3)
(3)
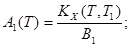 (4)
(4)
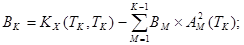
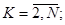 (5)
(5)
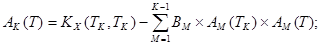
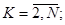 (6)
(6)
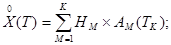
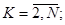 (7)
(7)
Здесь:
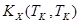 - корреляционная функция СП Х(Т), задающая /указывающая/ степень взаимосвязи между сечениями этого процесса с координатами ТК и ТМ;
- корреляционная функция СП Х(Т), задающая /указывающая/ степень взаимосвязи между сечениями этого процесса с координатами ТК и ТМ;
ВК - дисперсия случайной величины НК.
Использование данного алгоритма целесообразно только для случая формирования реализации случайных функций, характеризующихся относительно небольшим числом узлов дискретизации N и соизмеримостью длины реализации с интервалом корреляции случайной функции. Дело в том, что в противном случае указанный алгоритм оказывается неоправданно громоздким, так как при этом приходится запоминать двумерный массив координатных функций размером 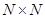 , большая часть которого заполнена нулями.
, большая часть которого заполнена нулями.
В то же самое время при решении задач воспроизведения реализаций случайных функций зачастую приходится иметь дело с реализациями, содержащими большое число узлов /несколько тысяч или даже десятков тысяч/, а интервалы корреляции процесса при этом обычно оказывается на несколько порядков меньше длины реализации.
Если корреляционная функция воспроизводимой случайной функции задана в  виде:
виде:
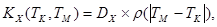 (8)
(8)
а нормированная корреляционная функция 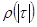 задана последовательностью своих в общем случае ненулевых значений
задана последовательностью своих в общем случае ненулевых значений 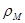 ,
, 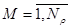 , т.е.
, т.е.
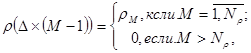 (9)
(9)
где 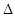 - шаг квантования реализации, то, как следует из анализа соотношений (5) – (7), для произвольного числа "к" область ненулевых значений координатной функции
- шаг квантования реализации, то, как следует из анализа соотношений (5) – (7), для произвольного числа "к" область ненулевых значений координатной функции 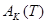 ограничена областью определения
ограничена областью определения 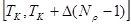 . Таким образом, координатная функция
. Таким образом, координатная функция 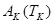 в общем случае отлична от нуля только при значениях М, принадлежащих интервалу
в общем случае отлична от нуля только при значениях М, принадлежащих интервалу 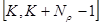 .
.
Но тогда формула (7) преобразуется к виду:
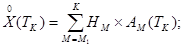
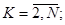 (10)
(10)
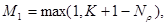 (11)
(11)
где под выражением МАХ(А, В) понимается максимум из величин А и В.
Таким образом, для формирования очередного к-ого значения центрированной случайной функции 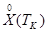 достаточно иметь информацию о значениях координатных функций
достаточно иметь информацию о значениях координатных функций 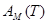 в узлах
в узлах 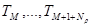 и дисперсией, что, в свою очередь, позволяет построить систему простых рекуррентных соотношений для расчета
и дисперсией, что, в свою очередь, позволяет построить систему простых рекуррентных соотношений для расчета 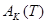 ,
, 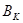 и
и 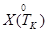 .
.
С этой целью вводятся в рассмотрение матрица А размерности 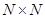 и массивы В, С и Р размерности N, предназначенные для хранения соответственно необходимых для проведения расчетов значений координатных функций
и массивы В, С и Р размерности N, предназначенные для хранения соответственно необходимых для проведения расчетов значений координатных функций 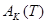 , дисперсии ВК, случайной функции
, дисперсии ВК, случайной функции 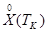 и среднеквадратических соотношений, равных
и среднеквадратических соотношений, равных 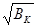 .
.
При к = 1:
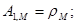
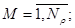
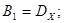
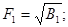
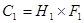
При к 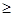 2:
2:
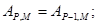
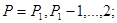
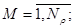
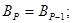
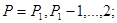
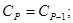
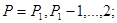
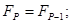
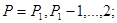
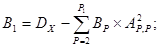 <
<