Кривые распределения. Критерии согласия.

Основной целью анализа вариационных рядов является выявление закономерности распределения, исключая при этом влияние случайных для данного распределения факторов. Этого можно достичь, если увеличивать объем исследуемой совокупности и одновременно уменьшать интервал ряда. При попытке изображения этих данных графически мы получим некоторую плавную кривую линию, которая для полигона частот будет являться некоторым пределом. Эту линию называют кривой распределения.

Иными словами, кривая распределения есть графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, которое функционально связано с изменением вариант. Кривая распределения отражает закономерность изменения частот при отсутствии случайных факторов. Графическое изображение облегчает анализ рядов распределения

Для оценки близости эмпирических и теоретических частот применяются критерий согласия Пирсона, критерий согласия Романовского, критерий согласия Колмогорова.

Наиболее распространенным является критерий согласия К. Пирсона, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам.

Выяснение общего характера распределения предполагает оценку степени его однородности, а также исчисление показателей асимметрии и эксцесса.

Ряды распределения могут иметь один и тот же центр группирования (показатели центра распределения) и одинаковые пределы варьирования признака (показатели вариации), однако при этом отличаться характером распределения единиц совокупности вокруг центра. Если большая часть совокупности расположена левее центра, имеет место левосторонняя асимметрия, если правее – правосторонняя.

Для оценки степени асимметричности применяют моментный и структурный коэффициенты асимметрии.

Моментный коэффициент асимметрии определяется по формуле:

А_S = 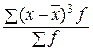: σ³.

На направление асимметрии указывает знак коэффициента: если А_S< 0, то это левосторонняя асимметрия (ее называют также отрицательной асимметрией), при правосторонней (положительной) асимметрии А_S> 0, если А_S = 0 – распределение симметричное. Чем больше абсолютная величина коэффициента, тем больше степень скошенности.

Рис. 2. А_S< 0 левосторонняя асимметрия Рис. 3. А_S > 0 правосторонняя асимметрия

Степень существенности асимметрии можно оценить с помощью средней квадратической ошибки коэффициента асимметрии,которая зависит от объема изучаемой совокупности и рассчитывается по формуле:

= ,

где п – число единиц в совокупности.

Если отношение > 3, асимметрия считается существенной и распределение признака в генеральной совокупности не является симметричным, если < 3, то асимметрия признается несущественной, вызванной влиянием случайных обстоятельств.

Структурные показатели асимметрии характеризуют асимметричность только в центральной части распределения, т. е. основной массы единиц, и в отличие от моментного коэффициента не зависят от крайних значений признака. Наиболее часто применяют структурный коэффициент асимметрии, предложенный английским статистиком К. Пирсоном:

А_S = .

 

В симметричном распределении Для симметричных распределений рассчитывается показатель эксцесса ( островершинности):

Е_Х = (: σ⁴) – 3.

Эксцесс может быть положительным и отрицательным. У островершинных распределений показатель эксцесса имеет положительный знак (+), а у плосковершинных – отрицательный знак (–). Предельным значением отрицательного эксцесса является значение Е_Х = – 2; величина положительного эксцесса может быть величиной бесконечной. В нормальном распределении Е_Х = 0.

Рис. 4. Е_Х < 0 плосковершинное распределение Рис. 5. Е_Х > 0 островершинное распределение

Средняя квадратическая ошибка эксцесса исчисляется по формуле:

=

где п – число наблюдений.

Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу кривых нормального распределения. Уравнение нормальной кривой:

,

где y_t – ордината кривой нормального распределения;

t – нормированное отклонение, равное ;

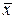– арифметическая средняя распределения;

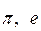– математические константы.

Рис. 6. Кривая нормального распределения

Нормальная кривая имеет огромное значение в теории выборочного метода, поскольку может быть показано, что средние стандартные отклонения, рассчитанные по случайным выборкам, тяготеют к нормальным в случае больших размеров выборок, если даже совокупность, из которой они взяты, сама не является нормально распределенной.

Особенности кривой нормального распределения:

1) кривая симметрична относительно максимальной ординаты, которая соответствует , ее величина равна ;

2) кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности. При этом, чем больше значения отклоняются от , тем реже они встречаются;

3) равновероятны одинаковые по абсолютному значению, но противоположные по знаку отклонения значений переменной х от :

а) кривая имеет две точки перегиба, находящиеся на расстоянии от ;

б) в промежутке (при t = 1) находится 68,3% всех значений признака; в промежутке (при t = 2) находится 95,4% всех значений признака; в промежутке (при t = 3) – 99,7% всех значений признака.

Порядок	По несгруппированным данным	По сгруппированным данным
Первый
Второй
Третий
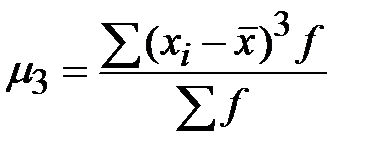
Четвертый

 

В нормальном (симметричном) распределении = 0, = Ме =Мо

При правосторонней асимметрии , > Ме > Мо

При левосторонней асимметрии , < Ме < Мо

M1 всегда = о в соответствии с нулевым сво-ом ср. арифметической и явл центром распределения.

М2 = диспресии

М3 при нормальном распределении = 0

С помощью критериев согласия, которые дают возможность установить, когда расхождения между теоретическими и эмпирическими частотами следует признать несущественными, т.е. случайными, а когда – существенными (неслучайными). Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой при выравнивании ряда гипотезы о характере распределения в эмпирическом ряду.

Критерий согласия Пирсона – один из основных:

где k – число групп, на которые разбито эмпирическое распределение,
– наблюдаемая частота признака в i-й группе,
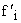– теоретическая частота.
Для распределения составлены таблицы, где указано критическое значение критерия согласия для выбранного уровня значимости 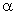и степеней свободы df.(или )
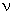Уровень значимости 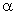– вероятность ошибочного отклонения выдвинутой гипотезы, т.е. вероятность того, что будет отвергнута правильная гипотеза. В статистике пользуются тремя уровнями:

• a= 0,10, тогда Р=0,90 (в 10 случаях их 100 может быть отвергнута правильная гипотеза);
• a= 0,05, тогда Р=0,95;
• a= 0,01, тогда Р=0,99.

 

Число степеней свободы df определяется как число групп в ряду распределения минус число связей: df = k –z. Под числом связей понимается число показателей эмпирического ряда, использованных при вычислении теоретических частот, т.е. показателей, связывающих эмпирические и теоретические частоты.
Например, при выравнивании по кривой нормального распределения имеется три связи:
; ; .
Поэтому при выравнивании по кривой нормального распределения число степеней свободы определяется как df = k –3.
Для оценки существенности расчетное значение 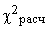сравнивается с табличным .
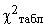При полном совпадении теоретического и эмпирического распределений , в противном случае >0. Если > , то при заданном уровне значимости и числе степеней свободы гипотезу о несущественности (случайности) расхождений отклоняем.
В случае, если , заключаем, что эмпирический ряд хорошо согласуется с гипотезой о предполагаемом распределении и с вероятностью Р=(1-a) можно утверждать, что расхождение между теоретическими и эмпирическими частотами случайно.
Критерий согласия Пирсона используется, если объем совокупности достаточно велик , при этом частота каждой группы должна быть не менее 5.

Критерий Романовского с основан на использовании критерия Пирсона, т.е. уже найденных значений , и числа степеней свободы df:

Он удобен при отсутствии таблиц для .
Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.

 

25. Способы и виды выборочного наблюдения. (!)

Тактика применения выборочного метода в экономико-статистических исследованиях использует следующие способы отбора единиц из генеральной совокупности:

а) индивидуальный отбор, при котором в выборку отбираются отдельные единицы;

б) групповой отбор – в выборку попадают качественно-однородные группы или серии изучаемых единиц;

в) комбинированный отбор – это комбинация индивидуального и группового отбора.

Каждый вид выборки может быть:

· повторным, при котором каждая отобранная единица или серия возвращаются в генеральную совокупность, и продолжает участвовать в дальнейшем отборе;

· бесповторным, при котором отобранная единица или серия в дальнейшем отборе не участвует.

В зависимости от способа отбора единиц выборочной совокупности различают четыре вида выборки:

1. Собственно-случайная выборка состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Принцип случайности попадания любой единицы генеральной совокупности в выборку предупреждает возникновение систематических (тенденциозных) ошибок выборки.

2. Механическая выборка отличается тем, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной, выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке – каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора генеральная совокупность, как бы механически разбивается на равновеликие группы, а из каждой такой группы в выборку попадает лишь одна единица.

3. При типической выборке генеральная совокупность вначале разбивается на однородные типические группы, затем из каждой такой группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Такая выборка обычно применяется при изучении сложных статистических совокупностей (при выборочном обследовании производительности труда работников, состоящих из отдельных групп по квалификации). Важной особенностью типической выборки является то, что она даёт более точные результаты по сравнению с другими способами отбора.

4. При серийной выборке из генеральной совокупности отбираются не отдельные единицы, а целые их серии (гнёзда). Внутри же каждой из попавшей в выборку серии обследуются все без исключения единицы, т.е. применяется сплошное наблюдение. Отбор отдельных серий в выборочную совокупность осуществляется либо посредством собственно-случайной выборки, либо механическим отбором. Практически серийная выборка производится, как правило, по схеме бесповторного отбора.

Одна из задач, решаемая на основе выборочного метода, ­определение ошибки выборки. В статистике принято определять среднюю (стандартную), предельную и относительную ошибки выборочного наблюдения. Ошибки выборки подразделяют на:

- ошибки регистрации, возникающие из-за неправильных или неточных сведений. Источниками таких ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении анкет, формуляров и т.д. Они достаточно легко обнаруживаются и устраняются. Среди ошибок регистра­ции выделяют:

- систематические (тенденциозные) ошибки, зависящие от организации выборочного исследования и обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам, сотням и т.д.);

- случайные (непреднамеренные) ошибки, связанные с природой любых статистических погрешностей и проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

- ошибки репрезентативности, возникающие из-за постоян­ного или спонтанного несоблюдения принципа случайного отбо­ра и которые также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором на­рушается основной принцип научно организованной выборки - принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выбороч­ной и генеральной совокупностей. Избежать ошибок репрезента­тивности нельзя, однако, пользуясь методами теории вероятно­стей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значе­ниям, границы которых устанавливаются с достаточно большой точностью. Изучение и измерение случайных ошибок репрезен­тативности - основная задача выборочного метода.

(Рис. 2)Определение необходимого(оптимального) объема выборки

 

Средняя ошибка выборки (µ - мю) равна:

 

для средней 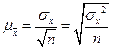; для доли ,

 

где р - доля определенного признака в генеральной совокупности.

Алгоритм анализа собст.-случайной выборки:

1.Определить сред ошибку выборки(М(мю)), для повторной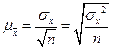

Для бесповторной Дописать

2.Определить предельную ошибку в выборке с определением выб. Вероятности.

∆= t * µ

3. Построить доверительный интервал для ген средней.

( – ∆) ( + ∆)

26. Определение генеральной средней по выборочной средней. (!)

Генеральная средняя

Пусть изучается дискретная генеральная совокупность относительно количественного признака X.

Генеральной средней называют среднее арифметическое значений признака генеральной совокупности.

Если рассматривать обследуемый признак X генеральной совокупности как случайную величину, то математическое ожидание признака равно генеральной средней этого признака:

Оценка генеральной средней по выборочной средней. Устойчивость выборочных средних.

Пусть из генеральной совокупности извлечена повторная выборка объема n со значениями признака .

Выборочная средняя есть несмещенная оценка генеральной средней.

Выборочная средняя является состоятельной оценкой генеральной средней.

Если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом и состоит свойство устойчивости выборочных средних.