Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является вариант, обладающий наибольшей частотой.
где:
Мо — значение моды
Хо — нижняя граница модального интервала
h — величина интервала
f m — частота модального интервала
f m-1 — частота интервала, предшествующего модальному
f m+1 — частота интервала, следующего за модальным
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. Центр упорядоченного вариационного ряда.
где:
- Me — искомая медиана
- X0 — нижняя граница интервала, который содержит медиану
- h — величина интервала
-
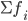— сумма частот или число членов ряда - S m-1 - сумма накопленных частот интервалов, предшествующих медианному
- fm — частота медианного интервала
Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.
Если Мо = Ме = Хср – то совокупность подчинена закону нормального распрделения
20. Вариационный ряд и его графическое изображение. Определение по графикам структурных характеристик.(!)
Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.
В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:
- Атрибутивными — называют ряды распределения, построенные по качественными признакам.
- Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называются вариационными.
Вариационный ряд распределения состоит из двух столбцов:
В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами и обозначаются Xi. Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.
Во втором столбце содержится количество конкретных вариант, выраженное через частоты или частости:
Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают fi. Сумма всех частот равна должна быть равна численности единиц всей совокупности.
Частости (Wi) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.
Ряды распределения изображаются в виде:
- Полигона (используется для изображения дискретных вариационных рядов) Прдствляет собой замкнутый многоуольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами – соот. или частоты или частости.
§ Гистограммы (одна из разновидностей столбиковых диаграмм), применяется для изображения интревально-вариационного ряда, который представляет из себя столбики с основаниями равными по ширине интервалов, и высотой, соответ. Частоте.
§ Кумуляты.(используется для графического изображения вариационных рядов. Изображается ряд накопленных частот за определенный промежуток времени.)
- Огивы - ломаная линия, соединяющая отрезки прямой, где ординаты – варианты, а абсциссы – накопленные частоты.