Основные геометрические соотношения в цепной передаче (рис. 3.3). Как указывалось выше, главным геометрическим параметром цепи и цепной передачи в целом является шаг t между осями шарниров цепи, равный расстоянию между центрами впадин между зубьями звездочек. Межосевое расстояние передачи выбирается в зависимости от шага цепи по следующему соотношению
. (3.1)
В этом выражении меньшие значения коэффициента в правой части соответствуют меньшим передаточным числам и наоборот.
Делительный диаметр d звездочки (диаметр окружности на которой лежат оси шарниров цепи, охватывающей звездочку) также зависит от шага цепи t
, (3.2)
где z –число зубьев звездочки.
В свою очередь число зубьев меньшей звездочки (её параметрам присвоим индекс «1 ») выбирают по эмпирическим соотношениям:
для роликовых и втулочных цепей
при условии z1 ³ 13; (3.3)
для зубчатых цепей
при условии z1 ³ 17; (3.4)
где u – передаточное число.
Число зубьев большей звездочки 
с округлением до ближайшего большего нечетного числа. При этом рекомендуется принимать число зубьев большей звездочки не более 120 для роликовых и втулочных цепей и не более 140 для зубчатых цепей.
Длину цепи Lр, выраженную в шагах (число звеньев цепи), для известного межосевого расстояния a можно вычислить по выражению
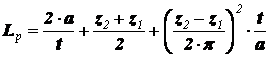. (3.5)
Полученное по выражению (3.5) значение необходимо округлить до ближайшего целого четного числа. При четном числе звеньев цепи и нечетных числах зубьев звездочек будет обеспечен наиболее равномерный износ как самих звездочек, так и шарниров цепи.
Далее по выбранному числу звеньев цепи необходимо уточнить межосевое расстояние передачи
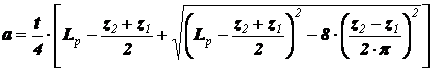. (3.6)
Полученное расчетом по (3.6) значение межосевого расстояния с целью исключения перенатяжения цепи из-за неточностей изготовления и монтажа сокращают на 0,2…0,4%, так чтобы свободная (ведомая) ветвь цепи имела некоторое провисание f (рис. 3.3). Для передачи, у которой угол q наклона межосевой линии к горизонту не превышает 40°, величина провисания ведомой ветви цепи 
, а для передач с углом 
- 
.
| Кинематика ЦП. |
Среднюю скорость Vц (м/с) цепи в цепной передаче можно определить по выражению
, (3.7)
где ni – частота вращения i -того вала, об/мин; zi – число зубьев звездочки, закрепленной на i -том валу; t – шаг цепи, мм.
Передаточное число u цепной передачи можно выразить через её кинематические и конструктивные показатели
, (3.8)
где w - угловая скорость звездочки, индекс «1 » соответствует ведущей звездочке, а «2 » - ведомой.
Передаточное отношение, вычисленное по (3.7) является средним за оборот, но в пределах поворота звездочки на один угловой шаг (2p/z) мгновенное передаточное отношение не остается постоянным. Для доказательства этого обратимся к схеме рис. 3.4.
Рис. 3.4. Схема совместного движения цепи и звездочки.
|
Пусть ведущая звездочка, имеющая z зубьев, вращается с угловой скоростью w=const по ходу часовой стрелки. Тогда тангенциальная скорость любой точки, лежащей на делительной окружности может быть найдена по известному соотношению
. (3.9)
Эта тангенциальная скорость всегда может быть представлена горизонтальной Vг и вертикальной Vв составляющими. Cоставляющие тангенциальной скорости звездочки для места входа шарнира цепи во впадину звездочки (на схеме рис. 3.4 левый шарнир верхней, набегающей, ветви цепи) и для предыдущего шарнира, уже движущегося совместно со звездочкой (на схеме рис. 3.4 правый верхний шарнир) по величине составляют
; 
;
Рис. 3.5. Относительная пульсация скорости цепи в зависимости от количества зубьев ведущей звёздочки.
|
где угол g составляет половину углового шага звездочки, то есть 
. Скорость движения цепи равна горизонтальной составляющей Vг и, следовательно, в этом положении цепи и звездочки несколько меньше тангенциальной скорости V0. После того как шарнир цепи попал во впадину звездочки он движется вместе с нею и после поворота звездочки на половину углового шага g его горизонтальная скорость движения сравняется с V0, а при последующем повороте звездочки ещё на полшага g эта скорость снова сократится до первоначального значения. Величина пульсации скорости цепи, равная отношению разности этих двух скоростей к средней скорости цепи в этом случае составит
. (3.10)
При подходе шарнира цепи к месту его входа в контакт с впадиной звездочки он имеет только горизонтальную скорость равную скорости цепи, а дно впадины между зубьями звездочки в момент встречи с шарниром цепи кроме горизонтальной имеет вертикальную скорость (см. схему рис. 3.4), следовательно их встреча произойдет с ударом. Соударение впадины звездочки с шарниром цепи ведет к возникновению микропластических деформаций в контактирующих поверхностях и, в конечном итоге, к усталостному изнашиванию этих поверхностей. Кроме того, соударение шарнира цепи со впадиной звездочки вызывает шум в работе передачи, а поперечные по отношению к ветви цепи движения шарнира генерируют в ней поперечные волновые колебания. Перечисленные отрицательные эффекты увеличиваются с уменьшением количества зубьев звездочки, это стало одной из причин ограничения числа зубьев звездочек с минимальной стороны (см. (3.3) и (3.4)).
Домашнее задание:
1. Прочитайте конспект
2. Выпишите в тетрадь геометрические параметры передачи