Матрицы. Операции над матрицами
Матрицей А размера m ´ n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:
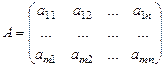 .
.
Числа этой таблицы называются элементами матрицы. aij – элемент, принадлежащий i- й строке и j- му столбцу, числа i, j называют индексами элемента.
Матрица, у которой количество строк совпадает с количеством столбцов (т.е. имеет размер n ´ n), называется квадратной.
Квадратная матрица вида: 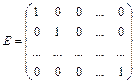 называется единичной.
называется единичной.
Транспонированной к матрице 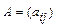 называется матрица
называется матрица 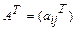 такая, что
такая, что 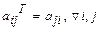 (т.е. все строки которой равны соответствующим столбцам матрицы
(т.е. все строки которой равны соответствующим столбцам матрицы 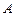 ).
).
Суммой 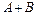
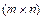 -матриц
-матриц 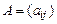 и
и 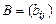 называется матрица
называется матрица 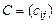 того же порядка, каждый элемент которой равен сумме соответственных элементов матриц А и В:
того же порядка, каждый элемент которой равен сумме соответственных элементов матриц А и В:
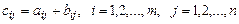 .
.
Произведением 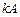 матрицы
матрицы 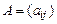 на число k называется матрица
на число k называется матрица 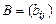 , получающаяся из матрицы А умножением всех ее элементов на k:
, получающаяся из матрицы А умножением всех ее элементов на k:
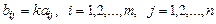 .
.
Произведением 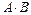
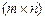 -матрицы
-матрицы 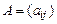 на
на 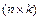 -матрицу
-матрицу 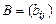 называется
называется 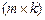 -матрица
-матрица 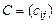 , элемент которой
, элемент которой 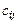 , стоящий в i –й строке и j –м столбце, равен сумме произведений соответственных элементов i –й строки матрицы А и j –го столбца матрицы В:
, стоящий в i –й строке и j –м столбце, равен сумме произведений соответственных элементов i –й строки матрицы А и j –го столбца матрицы В:
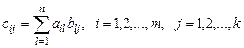 .
.
Для произведения двух матриц переместительный закон, вообще говоря, не выполняется: 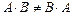 .
.
Пример.
Найти сумму, разность и произведения 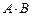 и
и 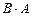 двух матриц, если
двух матриц, если 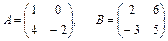 .
.
Решение.
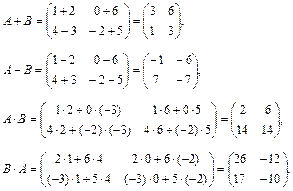
Пример.
Найти многочлен Р (А), если 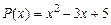 и
и 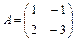 .
.
Решение.
Многочлен от матрицы имеет вид 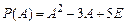 или
или
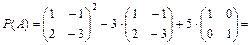
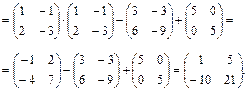
Задачи.
1.1. Вычислить линейные комбинации матриц 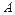 и
и 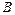 :
:
а) 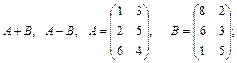
б) 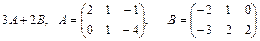 ;
;
в) 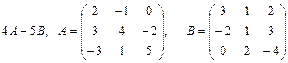 .
.
Вычислить:
1.2. 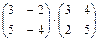 ; 1.3.
; 1.3. 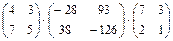 ;
;
1.4. 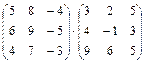 ; 1.5.
; 1.5. 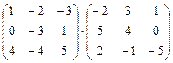 ;
;
1.6. 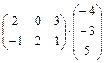 ; 1.7.
; 1.7. 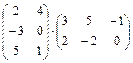 ;
;
1.8. 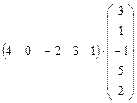 ; 1.9.
; 1.9. 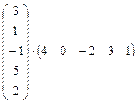 .
.
Найти произведения матриц 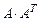 и
и 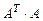 , если
, если
1.10. 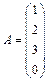 ; 1.11.
; 1.11. 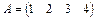 ;
;
1.12. 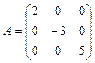 ; 1.13.
; 1.13. 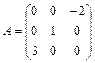 .
.
1.14. Найти значение многочлена 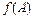 от матрицы
от матрицы 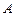 :
:
а) 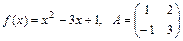 ;
;
б) 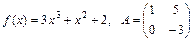 ;
;
в) 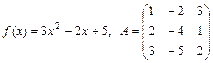 ;
;
г) 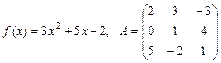 .
.
Определители
Определители 2-го и 3-го порядков
Для квадратных матриц существует понятие определителя матрицы.
|
|
Определителем 2-го порядка матрицы 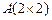 называется число:
называется число:
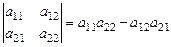 .
.
Определителем 3-го порядка матрицы 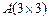 называется число:
называется число:
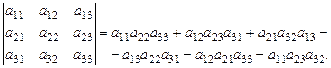
Определитель, соответствующий матрице А, обозначается также символами 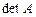 или
или 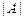 .
.
2.2. Определители n –го порядка
Алгебраическое дополнение 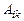 элемента
элемента 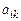 матрицы
матрицы 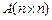 – это (с точностью до знака
– это (с точностью до знака 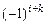 ) определитель
) определитель 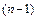 -го порядка, получающийся из исходного определителя вычеркиванием i –й строки и k –го столбца, на пересечении которых стоит элемент
-го порядка, получающийся из исходного определителя вычеркиванием i –й строки и k –го столбца, на пересечении которых стоит элемент 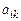 .
.
Определитель n –го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Например, разложение определителя 3-го порядка по элементам первой строки:
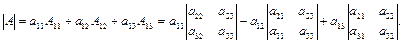
Для определителя n –го порядка соответственно получаем:
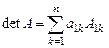 .
.
Свойства определителей
1. Определитель не изменится при транспонировании, т.е. 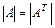 .
.
2. Общий множитель элементов какой-нибудь строки (или столбца) может быть вынесен за знак определителя.
3. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.
4. Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца), то определитель равен нулю.
5. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число.
6. Определитель треугольной матрицы (матрицы, у которой все элементы, расположенные по одну сторону одной из диагоналей, равны нулю) равен произведению элементов данной диагонали:
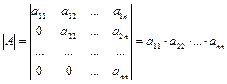 .
.
Задачи.
Вычислить определители 2-го порядка:
|
|
1.15. 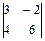 ; 1.16.
; 1.16. 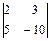 ;
;
1.17. 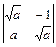 ; 1.18.
; 1.18. 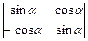 ;
;
1.19. 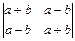 ; 1.20.
; 1.20. 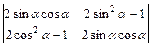 .
.
Решить уравнения:
1.21. 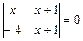 ; 1.22.
; 1.22. 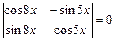 .
.
Вычислить определители 3-го порядка:
1.23. 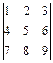 ; 1.24.
; 1.24. 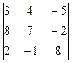 ;
;
1.25. 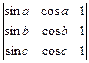 ; 1.26.
; 1.26. 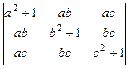 ;
;
1.27. 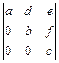 ; 1.28.
; 1.28. 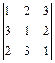 .
.
Решить неравенства:
1.29. 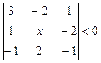 ; 1.30.
; 1.30. 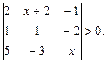
Упростить и вычислить определители:
1.31. 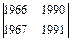 ; 1.32.
; 1.32. 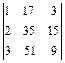 ;
;
1.33. 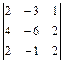 ; 1.34.
; 1.34. 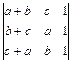 ;
;
1.35. 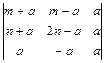 ; 1.36.
; 1.36. 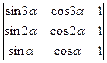 ;
;
1.37. 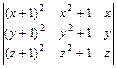 ; 1.38.
; 1.38. 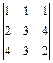 .
.
Вычислить определители, используя свойства определителей и разложение по строке или столбцу:
1.39. 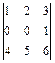 ; 1.40.
; 1.40. 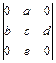 ;
;
1.41. 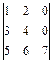 ; 1.42.
; 1.42. 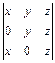 .
.
Вычислить определители:
1.43. 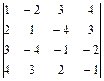 ; 1.44.
; 1.44. 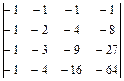 ;
;
1.45.  ; 1.46.
; 1.46. 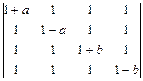 ;
;
1.47. 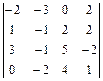 ; 1.48.
; 1.48. 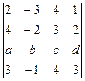 .
.
Обратная матрица
Квадратная матрица А называется вырожденной, если ее определитель равен нулю, и невырожденной в противном случае. Если А – невырожденная матрица, то существует и притом единственная матрица 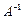 такая, что
такая, что
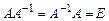 ,
,
где Е – единичная матрица. Матрица 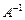 называется обратной к матрице А.
называется обратной к матрице А.
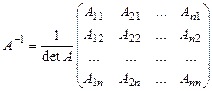 ,
,
где Aik – алгебраическое дополнение элемента аik матрицы А.
Для матриц размера 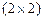 и
и 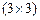 обратные матрицы имеют соответственно вид:
обратные матрицы имеют соответственно вид:
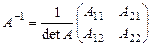 и
и 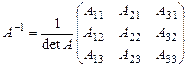 .
.
Пример.
Найти обратную матрицу к матрице 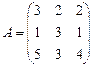 .
.
Решение.
Вычислим определитель матрицы А: 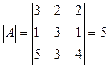 .
.
Найдем алгебраические дополнения элементов этого определителя:
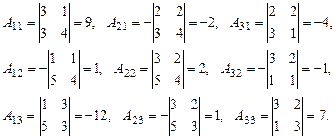
Следовательно, 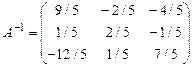 .
.
Задачи.
Найти матрицы обратные к матрицам:
1.49. 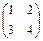 ; 1.50.
; 1.50. 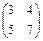 ;
;
1.51.  ; 1.52.
; 1.52. 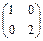 ;
;
1.53. 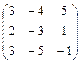 ; 1.54.
; 1.54. 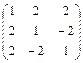 ;
;
1.55. 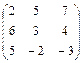 ; 1.56.
; 1.56. 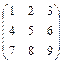 .
.
Решить матричные уравнения:
1.57. 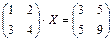 ;
;
1.58. 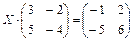 ;
;
1.59. 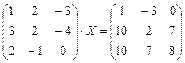 ;
;
1.60. 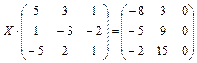 ;
;
1.61. 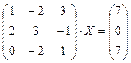 ; 1.62.
; 1.62. 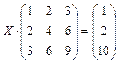 .
.
Ранг матрицы
Пусть в матрице А размера 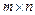 выбраны произвольно k столбцов и k строк
выбраны произвольно k столбцов и k строк 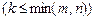 . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором k-го порядка матрицы А.
. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу порядка k, определитель которой называется минором k-го порядка матрицы А.
Максимальный порядок r отличных от нуля миноров матрицы А называется ее рангом, а любой минор порядка r, отличный от нуля, - базисным минором. Ранг матрицы А обозначается символом rang A.
|
|
Методы вычисления ранга матрицы
1. Метод окаймляющих миноров. Пусть в матрице найден минор k –го порядка М, отличный от нуля. Рассмотрим лишь те миноры 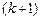 –го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор
–го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой минор 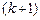 –го порядка, и вся процедура повторяется.
–го порядка, и вся процедура повторяется.
Пример.
Найти ранг матрицы А методом окаймляющих миноров, если
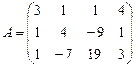 .
.
Решение.
Фиксируем минор 2-го порядка, отличный от нуля 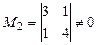 . Минор 3-го порядка
. Минор 3-го порядка 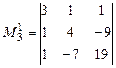 , окаймляющий минор М 2, равен нулю. Рассмотрим другой минор третьего порядка, окаймляющий М 2:
, окаймляющий минор М 2, равен нулю. Рассмотрим другой минор третьего порядка, окаймляющий М 2:
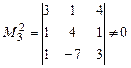 . Так как мы нашли неравный нулю минор 3-го порядка, то rang A = 3.
. Так как мы нашли неравный нулю минор 3-го порядка, то rang A = 3.
2. Метод элементарных преобразований. Этот метод основан на том факте, что элементарные преобразования матрицы не меняют ее ранга. Под элементарными преобразованиями понимают:
1) замену строк столбцами, а столбцов соответствующими строками (транспонирование);
2) перестановку строк матрицы;
3) вычеркивание строки, все элементы которой равны нулю;
4) умножение какой-либо строки на число, отличное от нуля;
5) прибавление к элементам одной строки соответствующих элементов другой строки.
Используя эти преобразования, матрицу можно привести к такому виду, когда все ее элементы, кроме 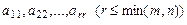 , равны нулю. Следовательно, ранг матрицы равен r.
, равны нулю. Следовательно, ранг матрицы равен r.
Пример.
Найти ранг матрицы 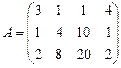 методом элементарных преобразований.
методом элементарных преобразований.
Решение.
Приведем матрицу к ступенчатому виду с помощью следующих элементарных преобразований. Поменяем местами 1-ую и 2-ую строки. Умножим элементы 1-ой строки на (-3) и прибавим к соответствующим элементам 2-ой строки. Затем умножим элементы 1-ой строки на (-2) и прибавим к соответствующим элементам 3-ой строки:
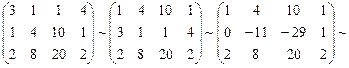
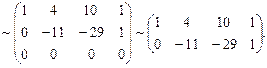
Ранг последней матрицы равен 2, так как, например, 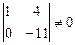 . Следовательно, ранг исходной матрицы также равен 2: rang A = 2.
. Следовательно, ранг исходной матрицы также равен 2: rang A = 2.
Задачи.
Найти ранг матрицы методом окаймляющих миноров:
1.63. 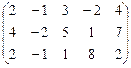 ; 1.64.
; 1.64. 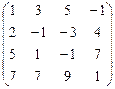 ;
;
1.65. 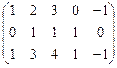 ; 1.66.
; 1.66. 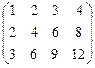 .
.
Найти ранг матрицы методом элементарных преобразований:
1.67. 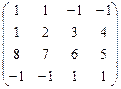 ; 1.68.
; 1.68. 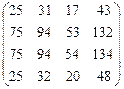 ;
;
1.69. 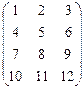 ; 1.70.
; 1.70. 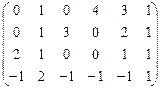 ;
;
1.71. 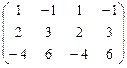 ; 1.72.
; 1.72. 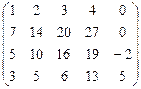 .
.