Метод наименьших квадратов

Практическое занятие №5. Метод наименьших квадратов.

Цель работы: построение уравнений регрессии методом средних и наименьших квадратов.

Теоретическая часть

Уравнение регрессии

Задача линейного регрессионного анализа состоит в том, что зная положение точек на плоскости, так провести линию регрессии, что бы сумма квадратов отклонения вдоль ординаты этих точек от проведенной прямой была минимальной. Можно использовать различные способы (метод наименьших квадратов, метод средних, графический метод). Для проведения вычислений по методы наименьших квадратов к выдвигаемой гипотезе или форме уравнения регрессии выдвигаются следующие требования:

- это уравнение должно быть линейным попараметром или допускать возможность линеаризации.

Пусть уравнение вида

и ,

Это расчетное значение, следовательно, аналитически задачу наименьших квадратов можем выразить

, где

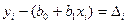, или

Необходимо вычислить частные производные и прировнять их к нулю. Решая эту системы, находим коэффициенты регрессии b0 и b1. Эта система называется системой нормальных уравнений.

Если подставить в системы значения U и продифференцируем, то получим системы следующего вида

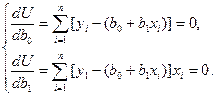
Преобразуем систему нормальных уравнений

Если уравнение вида

, , ,

Метод средних

Данный метод имеет ограниченное применение. Используется только в парных ситуациях y = f(x). Данный метод состоит в следующем – выполнение условия равенства нулю всех отклонений наблюдаемой величины суммы всех отклонений наблюдаемой величины от среднего значения.

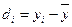
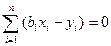
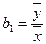, где

, где ,

Преимущество данного метода заключается в его простоте, не накладывает ограничение на исходные опытные данные (например, что бы эти данные имели нормальное распределение).

Если зависимость вида, то для получения нужного количества уравнений выбирают из общего количества пар наблюдений примерно половину и сумму их отклонений приравнивают к нулю, а затем сумму прочих отклонений

,

В итоге получаем систему уравнений вида

, где при четном n и при n нечетном.

Сложив эти два уравнения, получаем уравнение вида

Разделив все члены уравнения на N, получаем

Если представить зависимость в виде

, то коэффициент регрессии можно вычислить по одной из формул

, или

На практике при нечетном N второе из уравнений составляют в виде

Этот прием делает метод средних однозначным.

Если зависимость вида, то

 

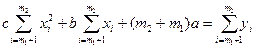
Пример: Произвести регрессионный анализ для выборки, представленной в таблице 5.1 с помощью методов средних и наименьших квадратов.

 

Таблица 5.1 – Значения выборки

№	X	Y
		8,81
		7,4
		6,1
		4,89
		3,88
		3,02
		2,3

Ход выполнения работы

Вид уравнения	Метод	B0	B1	Sост
1. Y = b1x	Средних		0,0325	5,85
Квадратов		0,0338	5,532
2. Y = b0+b1x	Средних	-3,555	0,0545	0,447
Квадратов	-3,517	0,0544	0,438
3. Y = b0x+b1x2	Средних	0,00675	0,00015	0,026
Квадратов	0,00726	0,000148	0,016

Метод средних

1. Y = b₁x

Y_g = b₁x

№	X	Yg	Yr	Yg-Yr	(Yg-Yr)2
		8,81	7,150	1,66	2,7556
		7,4	6,500	0,9	0,81
		6,1	5,850	0,25	0,0625
		4,89	5,200	-0,31	0,0961
		3,88	4,550	-0,67	0,4489
		3,02	3,900	-0,88	0,7744
		2,3	3,250	-0,95	0,9025
		36,4			5,85

 

2. Y = b₀+b₁x

Для четного делим на две равные системы. Для нечетного центральный элемент включаем в обе системы.:

 

b₀+220b₁ = 8,81

b₀+200b₁ = 7,40

b₀+180b₁ = 6,10

b₀+160b₁ = 4,89

_____________

 

b₀+160b₁ = 4,89

b₀+140b₁ = 3,88

b₀+120b₁ = 3,02

b₀+100b₁ = 2,30

------------------------------------------- (суммируем)

------------------------------------------- (решаем)

 

№	X	Yg	Yr	Yg-Yr	(Yg-Yr)2
		8,81	8,435	0,375	0,141
		7,4	7,345	0,055	0,003
		6,1	6,255	-0,155	0,024
		4,89	5,165	-0,275	0,076
		3,88	4,075	-0,195	0,038
		3,02	2,985	0,035	0,001
		2,3	1,895	0,405	0,164
		36,4			0,447

 

3. Y = b₀x+b₁x²

Проводим линеаризацию:

 

Подставляем исходные значения x и y, делим на две системы:

0,040=b₀+220*b₁

0,037=b₀+200*b₁

0,034=b₀+180*b₁

0,030=b₀+160*b₁

-----------------------

0,030=b₀+160*b₁

0,027=b₀+140*b₁

0,025=b₀+120*b₁

0,023=b₀+100*b₁

----------------------- Суммируем

--------------------------------Решаем

 

№	X	Yg	Yr	Yg-Yr	(Yg-Yr)2
		8,81	8,745	0,065	0,004
		7,4	7,350	0,050	0,003
		6,1	6,075	0,025	0,001
		4,89	4,920	-0,030	0,001
		3,88	3,885	-0,005	0,000
		3,02	2,970	0,050	0,003
		2,3	2,175	0,125	0,016
		36,4			0,026

 

Метод наименьших квадратов

1. Y = b₁x

 

№	X	Yg	Yg*X	X2	Yr	Yg - Yr	(Yg – Yr)2
		8,81	1938,2		7,434	1,376	1,892
		7,4			6,759	0,641	0,411
		6,1			6,083	0,017	0,000
		4,89	782,4		5,407	-0,517	0,267
		3,88	543,2		4,731	-0,851	0,724
		3,02	362,4		4,055	-1,035	1,072
		2,3			3,379	-1,079	1,165
			6434,2				5,532

2.Y = b₀+b₁x

 

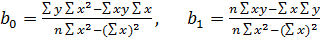
№	X	Yg	X2	XY	Yr	Yg - Yr	(Yg – Yr)2
		8,81		1938,2	8,469	0,341	0,116
		7,4			7,379	0,021	0,000
		6,1			6,290	-0,190	0,036
		4,89		782,4	5,200	-0,310	0,096
		3,88		543,2	4,110	-0,230	0,053
		3,02		362,4	3,021	-0,001	0,000
		2,3			1,931	0,369	0,136
		36,4		6434,2			0,438

 

 

\

3. Y = b₀x+b₁x²

0,00726

0,00014834

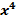
№	X	Yg						Yr	Y-Yr	(Y-Yr)2
		8,81				1938,2		8,778304	0,031696	0,001005
		7,4						7,386897	0,013103	0,000172
		6,1						6,114166	-0,01417	0,000201
		4,89				782,4		4,960111	-0,07011	0,004916
		3,88				543,2		3,924732	-0,04473	0,002001
		3,02				362,4		3,008028	0,011972	0,000143
		2,3						2,210001	0,089999	0,0081
						6434,2				0,016537