Для определения погрешности с которой находятся решения дифференциального уравнения 
на данном отрезке используется способ двойного счета:
- Находим значения
для всех xi из отрезка 
с заданным шагом h. - Находим значения
для всех xi из отрезка с шагом h/2. - Погрешность каждого найденного определяется по формуле
a) Метод Эйлера: 
;
b) Метод Эйлера – Коши: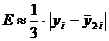 
;
c) Метод Рунге – Кутта: 
Задание
1. В среде Mathcad решить данное обыкновенное дифференциальное уравнение на с шагом h и начальным условием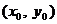 
:
· Методом Эйлера;
· Методом Эйлера – Коши;
· Методом Рунге – Кутта.
Предусмотреть вывод погрешности каждого шага.
| Вариант | f(x, y) | x0=a | xn=b | y0 | h | Вариант | f(x, y) | x0=a | xn=b | y0 | h | |
| 1. | x2+sin(y/2) | 0,7 | 0,1 | 9. | 2xy/(x+4)-0,4 | 1,7 | 0,2 | |||||
| 2. | 
| 2,6 | 4,6 | 1,8 | 1,2 | 10. | 
| 2,9 | 0,2 | |||
| 3. | cos(1,5x-y2)-1,3 | -1 | 0,2 | 0,2 | 11. | x+2,5y2+2 | 0,9 | 0,1 | ||||
| 4. | x2+xy+y2 | 1,2 | 0,1 | 12. | 2-sin(x+y)2 | 2,3 | 0,1 | |||||
| 5. | 4,1x-y2+0,6 | 0,6 | 2,6 | 3,4 | 0,2 | 13. | x2y-y2 | 0,6 | 0,1 | |||
| 6. | 1/(1+x3y)+2y | 1,5 | 2,1 | 0,05 | 14. | sin(1,5x-y2) | -1 | 0,2 | 0,2 | |||
| 7. | 2,5x+cos(y+0,6) | 1,5 | 0,2 | 15. | 2x-y2+0,8 | 0,5 | 2,5 | 0,5 | ||||
| 8. | x+cos(y/2) | -2 | -1 | 0,1 | 16. | 3+sin(x+y)2 | -1 | 0,2 |
Тесты
Для метода Эйлера обычного и с двойным просчетом)
f(x,y)=cosy+3x, a=0, b=1, y0=1,3, n=5
| x | 0,2 | 0,4 | 0,6 | 0,8 | ||
| y | 1,3535 | 1,5166 | 1,7674 | 2,0884 | 2,4694 | |
| e | 0,0274 | 0,0442 | 0,0533 | 0,0582 | 0,0638 |
Для метода Эйлера-Коши с двойным просчетом)
f (x,y)=y*(1-x), a=0, b=0,5, y0=1, n=5
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| y | 1,0095 | 1,1969 | 1,2900 | 1,3766 | 1,4544 | |
| e | 0,000004 | 0,00008 | 0,00010 | 0,00013 | 0,00015 |
Для метода Рунге-Кутта)
f(x,y)=y*(1-x), a=0, b=0,5, y0=1, n=5
| x | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | |
| y | 1,0997 | 1,1972 | 1,2905 | 1,3771 | 1,4549 |
Порядок выполнения работы
5.1. Изучить теоретические сведения, необходимые для выполнения заданий.
5.2. Написать текст программы в среде программирования Delphi. Выполнить запуск программы исправить ошибки при их обнаружении.
5.3. Выполнить тестовые задания.
5.4. Выполнить задания, соответствующие вашему варианту (по номеру компьютера).
5.5. Сохранить программу в своей папке.
5.6. Выполнить отчет о работе в письменном виде на листах формата А4.
5.7. Подготовить ответы на контрольные вопросы.
Отчет о выполненной работе
6.1. Отчет о выполненной работе должен содержать:
1. Номер и название лабораторной работы.
2. Цели работы.
3. Условия заданий.
4. Тексты программ Вашего варианта с результатами.
6.2. Защита лабораторной работы осуществляется в следующем порядке:
1. Ответы на вопросы преподавателя по выполненным заданиям.
2. Ответы на контрольные вопросы преподавателю.
7. Контрольные вопросы
7.1. Дифференциальные уравнения какого вида решаются изученными численными методами?
7.2. Какие данные являются исходными, и что является результатом в программах решения таких дифференциальных уравнений?
7.3. Формула метода Эйлера. Поясните смысл всех параметров и переменных входящих в формулу.
7.4. Формула метода Эйлера-Коши. Поясните смысл всех параметров и переменных входящих в формулы.
7.5. В чем суть метода двойного просчета при решении обыкновенных дифференциальных уравнений?
7.6. Для чего в программах решения дифференциальных уравнений используется двойной просчет?
7.7. Формула метода Рунге – Кутта. Поясните смысл всех параметров и переменных входящих в формулы.
7.8. Какой из изученных методов численного дифференцирования является наиболее точным?
Литература
1. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Численные методы. – М.: ACADEMA, 2004.
2. Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании. – М.: Финансы и статистика,. 2002.
3. Турчак Л.И., Плотников П.В. Основы численных методов. – М.: ФИЗМАТЛИТ, 2003.
4. Каханер Д., Моулен К., Неш С. Численные методы и программное обеспечение. – М.: Мир, 2001.
5. Воробьёва Г.Н., Данилова А.Н. Практикум по вычислительной математике. – М.: Высшая школа, 1990.
6. Архангельский А.Я. Программирование в Delphi 6. - М.: Бином, 2004.
7. Хомоненко А., Гофман В. и др. Delphi 7. - СПб: БХВ-Петербург, 2004.
8. Delphi. Советы программистам. / Под редакцией В. Озерова. - СПб: Символ, 2003.
9. Культин Н. Основы программирования в Delphi 7. - СПб: БХВ-Петербург, 2004.
10. Жуков А. Изучаем Delphi. - СПб: Питер, 2000.