Расчетная нагрузка колеса на рельс

Динамическая максимальная нагрузка не превышает расчетную нагрузку, расчетное значение колесной нагрузки вычисляется через ее среднее значение Р _ср и среднеквадратическое отклонение S:

 

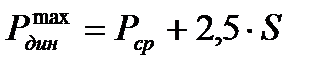(2)

 

(3)

где P _ст – статическая нагрузка колеса на рельс (P _ст = 102500 Н),

- средняя величина нагрузки, возникающая за счет вертикальных колебаний кузова на рессорах, принимаемая на основании опытных данных ЦНИИ.

(4)

где - динамическая максимальная нагрузка колеса на рельс от вертикальных колебаний надрессорной части экипажа.

(5)

где q _к – вес необрессоренной части экипажа, приходящийся на одно колесо (q _к =19250 Н),

k _д – коэффициент динамических добавок от вертикальных колебаний надрессорной части.

(6)

где v – скорость движения (v = 44,44 м/с),

f _ст – статический прогиб рессорного подвешивания (f _ст = 0,12 м).

.

 

Среднеквадратическое отклонение динамической нагрузки колеса на рельс S от нескольких факторов определяется из суммы дисперсий,

(7)

где S _р – среднеквадратическое отклонение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорной части экипажа,

S _нп – среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренных масс при прохождении колесом изолированной неровности пути,

S _ннк – среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренных масс из-за наличия нероерывных неровностей на поверхности катания колес,

S _инк – среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренных масс, возникающих из-за наличия изолированных неровностей на поверхности катания колес,

q ₁ – доля колес, имеющих изолированные неровности, от общего числа однотипных колес, остальные из которых имеют непрерывные неровности (q ₁ = 0,05).

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Среднеквадратическое отклонение нагрузки, возникающей за счет колебания кузова на рессорах, принимается на основании опытных данных ЦНИИ:

(8)

 

Среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренных масс при прохождении колесом изолированной неровности пути:

(9)

где - максимальное значение силы инерции,

(10)

где a₁ – коэффициент, учитывающий изменение колеблющейся массы пути на железобетонных шпалах по сравнению с путем на деревянных шпалах (a₁=0,931),

b - коэффициент, учитывающий влияние типа рельса на возникновение динамической неровности по отношению к рельсу типа Р50,

(11)

Изм.

Лист

№ докум.

Подпись

Дата

Лист

где I _Р – момент инерции рельса рассматриваемого типа при износе 0мм (b = 0,87),

e - коэффициент, учитывающий влияние жесткости пути на образование динамической неровности пути по сравнению с деревянными шпалами (e = 0,322),

g - коэффициент, учитывающий влияние рода балласта на образование динамической неровности пути (g = 1),

l _ш – расстояние между осями шпал (l _ш = 0,55 м).

;

.

Среднеквадратическое отклонение динамической нагрузки на рельс от сил инерции необрессоренной массы, возникающих из-за наличия изолированных неровностей на поверхности катания колес:

(12)

где - максимальное значение силы инерции.

(13)

где k ₁ – коэффициент, характеризующий степень неравномерности образования проката поверхности катания колес (k ₁ = 0,23),

a₀ – коэффициент, учитывающий влияние колеблющейся массы пути (a₀ = 0,403),

d – диаметр колеса (d = 1,25 м).

,

.

Среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренных масс, возникающих из-за наличия изолированных неровностей на поверхности катания колес:

(14)

где - максимальное значение силы инерции.

(15)

где y_max – наибольший дополнительный прогиб рельса при вынужденных колебаниях катящегося по ровному рельсу колеса с изолированной неровностью на поверхности катания.

(16)

где е – расчетная глубина плавной изолированной неровности на поверхности катания колеса (е = 0,00047 м).

,

Изм.

Лист

№ докум.

Подпись

Дата

Лист

 

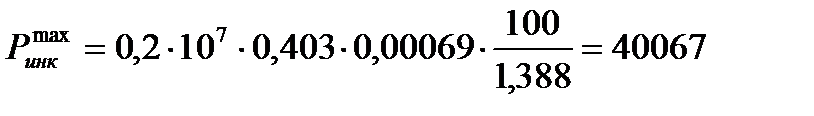
Эквивалентные нагрузки

При движении поезда на путь воздействует система сосредоточенных сил – давлений от колес тележек. Самыми невыгодными положениями такой подвижной нагрузки для расчетного сечения является расположение одного из колес на вершине линии влияния. Нагрузку, определяемую как сумму воздействий усилий от каждого из включенных в расчетную схему колес в данном сечении, называют эквивалентной нагрузкой.

 

Рис. 3.1 – Расположение эквивалентной силы

 

Максимальная эквивалентная нагрузка для расчетов напряжений в рельсах от изгиба определяется:

(17)

где - ординаты линии влияния изгибающих моментов рельса в сечениях пути, расположенных под колесными нагрузками от осей, смежных с расчетной осью.

. (18)

 

Риc. 3.2 – Схема определения эквивалентной нагрузки при расчете изгибающего момента

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

x₁= l₁ = 2,4 м, x₂= l₂= 4,6 м,

где l₁ и l₂ – расстояние соответственно между первой и второй, второй и третьей осями тележки.

,

,

 

 

Рис. 3.3 – Схема определения эквивалентной нагрузки при расчете изгибающего момента

 

Эквивалентная нагрузка для определения прогиба рельса рассчитывается аналогичным способом. Максимальная эквивалентная нагрузка определяется:

(19)

где - ординаты линии влияния прогибов рельса в сечениях пути, расположенных под колесными нагрузками от осей, смежных с расчетной осью.

, (20)

 

 

Рис. 3.4 – Схема определения эквивалентной нагрузки при расчете прогиба

 

,

,

.

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

 

 

Рис. 3.5 – Схема определения эквивалентной нагрузки при расчете прогиба