Математический факультет
Кафедра информатики и прикладной математики
Курсовая работа НА ТЕМУ:
«ОЦЕНИВАНИЕ СМЕЩЕНИЯ СТАТИСТИКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МНОГОМЕРНОГО ВРЕМЕННОГО РЯДА»
Брест 2009
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
2. ОЦЕНИВАНИЕ СМЕЩЕНИЯ СТАТИСТИКИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
3. ОКНА ПРОСМОТРА ДАННЫХ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ПРИЛОЖЕНИЕ
ВВЕДЕНИЕ
Современный этап развития теории вероятностей и математической статистики характеризуется значительным расширением теоретических исследований по статистическому спектральному анализу (анализу в частной области) временных рядов и их практическим применением во многих областях человеческой деятельности, таких, как экономика, спектроскопия, медицина, биология, страхование, финансы, социология, радиоэлектроника, электротехника, геофизика, геология и многие другие. Цели изучения временных рядов могут быть различными. Можно, например, стремиться предсказывать будущее на основании знания прошлого, управлять процессом, порождающим ряд, выяснить механизм, порождающий ряд, или просто сжато описать характерные особенности ряда. Поэтому под статистическим спектральным анализом временных рядов понимают статистический спектральный анализ стационарных случайных процессов.
Одной из главных задач спектрального анализа временных рядов является построение и исследование оценок спектральных плотностей стационарных случайных процессов, так как они дают важную информацию о структуре процесса.
Существуют параметрические и непараметрические методы спектрального анализа. Среди непараметрических методов выделяют метод, в котором для построения оценки спектральной плотности производится осреднение периодограмм, построенных по непересекающимся интервалам исходной последовательности наблюдений и вводятся окна просмотра данных для уменьшения смещения оценок.
|
|
В данной работе оцениваются смещения статистики взаимной спектральной плотности. Построены графики оценки спектральной плотности для последовательности наблюдений - солнечной активности по Вольфу с 1749 г. по 1901 г.
Также построены графики для центрированного случайного процесса.
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РАБОТЕ
Временным рядом называют последовательность наблюдений, обычно упорядоченную во времени, хотя возможно упорядочение и какому-то другому параметру.
Совокупность функций вида
назовём r-компонентным векторным временным рядом (r-мерным временным рядом).
Переменная t обычно соответствует времени выполнения или регистрации наблюдений и измерений.
Действительным случайным процессом 
= 
называется семейство случайных величин, заданных на вероятностном пространстве 
, где 
, 
, 
- некоторое параметрическое множество.
Если 
, или подмножество из 
, то говорят, что 
, - случайный процесс с дискретным временем.
Если 
, или подмножество из 
, то говорят, что , 
- случайный процесс с непрерывным временем.
Аргумент 
чаще всего интерпретируется как время, хотя при решении практических задач он может иметь и другое смысловое значение.
При каждом фиксированном 
, 
, - множество случайных величин.
|
|
Если в определении случайного процесса 
, 
, 
, то = 
называется 
-мерным случайным полем.
Введем характеристики случайного процесса , , во временной области.
Математическим ожиданием случайного процесса 
, , называется функция вида
, .
Дисперсией случайного процесса 
, , называется функция вида
, .
Корреляционной функцией случайного процесса 
, , называется функция вида
, 
.
Ковариационной функцией случайного процесса , , называется функция вида
.
Заметим, что если 
, то 
, 
.
Смешанным моментом 
го порядка, 
, случайного процесса , 
, называется функция вида
, 
, 
.
Заметим, что
, 
.
Пусть 
- значения случайного процесса в точках 
.
Смешанный момент го порядка, , можно также определить как
, , .
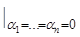Смешанным семиинвариантом (кумулянтом) го порядка, , случайного процесса , , называется функция вида
, , ,
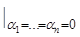которую также будем обозначать как 
.
Между смешанными моментами и смешанными семиинвариантами го порядка, , существуют связывающие их соотношения, которые имеют вид
(1.1)
(1.2)
суммирование по всевозможным разбиениям множества 
.
Спектральной плотностью случайного процесса , 
, называется функция вида
= 
, 
,
при условии, что
.
Из определения видно, что спектральная плотность 
непрерывная, периодическая функция с периодом, равным 
по каждому из аргументов.
Семиинвариантной спектральной плотностью 
го порядка, , случайного процесса 
, , называется функция вида
= 
, 
,
при условии, что
.
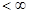Лемма 1. Для любого целого 
справедливо соотношение
|
|
(1.3)
Теорема 1. Для смешанного семиинварианта 
го порядка, 
, случайного процесса 
справедливы представления
, (1.4)
Доказательство. Домножая обе части соотношения (1.1) на
, 
,
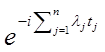и интегрируя обе части полученного неравенства по 
на 
, получим
.
Используя лемму 1, получим при 
требуемый результат. Теорема доказана.
Лемма 2. Если функция 
интегрируема и периодична с периодом 
, то для любого действительного 
имеет место соотношение
Доказательство. Предположим, что >0. Можно записать
В третьем слагаемом правой части последнего равенства сделаем замену переменных интегрирования 
и, учитывая периодичность с периодом 
функции , получаем требуемое. Случай, когда <0, доказывается аналогично. Лемма доказана.
Спектральной плотностью случайного процесса 
, 
, называется функция вида
= 
, 
,
при условии, что
.
Из определения видно, что спектральная плотность 
непрерывная, периодическая функция с периодом, равным 
по каждому из аргументов.