Рассмотрим действительный стационарный в широком смысле случайный процесс 
, 
, с математическим ожиданием 
, 
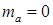, взаимной ковариационной функцией 
, и взаимной спектральной плотностью 
.
Предположим, имеются Т последовательных, полученных через равные промежутки времени наблюдений 
за составляющей 
, рассматриваемого процесса 
. Как оценку взаимной спектральной плотности в точке 
рассмотрим статистику
(2.1)
где 
, - произвольная, не зависящая от наблюдений четная целочисленная функция, 
для 
, а
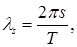(2.2)
s – целое число, 
- целая часть числа 
.
Статистика 
, называемая выборочной взаимной спектральной плотностью или периодограммой, задается соотношением
(2.3)
определено равенством (2.2).
Известно, если рассматривать как оценку взаимной спектральной плотности 
в точке 
, то она является асимптотически несмещенной, но не состоятельной оценкой этой спектральной плотности. Заметим, что оценка (2.1) взаимной спектральной плотности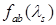 
построена путем осреднения значений периодограммы в точках 
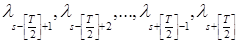некоторой весовой функцией 
.
Лемма 3. Для любого действительного 
, и любого 
справедливо неравенство
где 
- ядро Фейера, задаваемое равенством
(2.4)
, а
, (2.5)
Доказательство. Учитывая чётность функции 
и элементарное неравенство
(2.6)
справедливое для всех x, таких, что 
, имеем
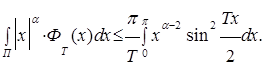
Сделаем замену переменной интегрирования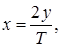 
тогда правая часть последнего неравенства примет вид
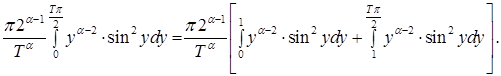
Применив для оценки первого интеграла, стоящего в квадратных скобках, неравенство 
, а для оценки второго – неравенство 
, получим
Лемма доказана.
Проведен численный анализ для соотношения (2.5) при Т=100 и при 
, T 
, где T - число наблюдений и получены следующие результаты
| 
| 
|
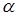
| 0,1 | 0.663138 | 2.13239 |
| 0,2 | 0.447986 | 1.48005 |
| 0,3 | 0.308154 | 1.04694 |
| 0,4 | 0.216092 | 0.7554 |
| 0,5 | 0.154768 | 0.556644 |
| 0,6 | 0.113483 | 0.41954 |
| 0,7 | 0.085422 | 0.323925 |
| 0,8 | 0.06619 | 0.256576 |
| 0,9 | 0.0529213 | 0.208718 |
| 0.0437283 | 0.348932 |
| α | 
| 
|
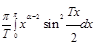
| 0,1 | 0.663138 | 1.63184 |
| 0,2 | 0.447986 | 1.10052 |
| 0,3 | 0.308154 | 0.755087 |
| 0,4 | 0.216092 | 0.527538 |
| 0,5 | 0.154768 | 0.375825 |
| 0,6 | 0.113483 | 0.273535 |
| 0,7 | 0.085422 | 0.203842 |
| 0,8 | 0.06619 | 0.155894 |
| 0,9 | 0.0529213 | 0.122613 |
| 0.0437283 | 0.0993358 |
ОКНА ПРОСМОТРА ДАННЫХ
Для выделения определенных характеристик спектральных оценок, нередко прибегают к сглаживанию значений на концах случайного временного ряда. Временное сглаживание представляет собой умножение ряда на «окно данных».
При определении расширенного конечного преобразования Фурье, задаваемого соотношением
введена функция 
, называемая окном просмотра данных (множителем сходимости, коэффициентом сглаживания).
Функцию
(3.1)
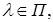называют частотным окном. Из соотношения (3.1) вытекает, что
Характерное поведение функции 
состоит в том, что она становится все более сконцентрированной в окрестности нуля при 
.
Примеры окон просмотра данных:
1. 
1 – окно Дирихле;
2. 1- 
– окно Фейера;
3. 
;
4. 
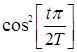– окно Хэннинга;
5. 
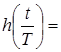
– окно Хэмминга;
6. 
– окно Хэмминга;
7. 
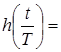
, где 
– окно Хэмминга;
8. 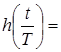1-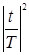 
– окно Рисса.
ЗАКЛЮЧЕНИЕ
В данной работе исследована оценка спектральной плотности вида
где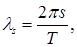 
, а периодограмма задана следующим соотношением
Оценивается смещение данной спектральной плотности. Построены графики этой оценки для различных окон данных на основании наблюдений за солнечной активностью по Вольфу с 1749 г. по 1901 г.
Также построены графики для центрированного случайного процесса.