Самоорганизованные сети Кохонена

Нейронные сети Кохонена

Нейронные сети Кохонена считаются отдельным классом нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «победитель забирает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.

По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена. Наиболее известные из них:

· Сети векторного квантования сигналов^[, тесно связанные с простейшим базовым алгоритмом кластерного анализа (метод динамических ядер или K-средних);

· Самоорганизующиеся карты Кохонена (Self-Organising Maps, SOM);

· Сети векторного квантования, обучаемые с учителем (Learning Vector Quantization).

Слой Кохонена состоит из некоторого количества 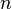параллельно действующих линейных элементов. Все они имеют одинаковое число входов и получают на свои входы один и тот же вектор входных сигналов 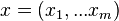. На выходе -го линейного элемента получаем сигнал

 

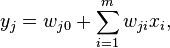
где 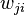— весовой коэффициент го входа го нейрона, — пороговый коэффициент.

После прохождения слоя линейных элементов сигналы посылаются на обработку по правилу «победитель забирает всё»: среди выходных сигналов ищется максимальный; его номер . Окончательно, на выходе сигнал с номером равен единице, остальные — нулю. Если максимум одновременно достигается для нескольких , то либо принимают все соответствующие сигналы равными единице, либо только первый в списке (по соглашению). «Нейроны Кохонена можно воспринимать как набор электрических лампочек, так что для любого входного вектора загорается одна из них.»

Разработчиками теории искусственных нейронных сетей считаются Маккалон и Питтс.

Основные результаты теории нейронных сетей в начале её становления сводились к следующему:

1. Модель нейрона в виде простейшего процессорного элемента, который вычисляет значение некоторой функции.

2. Конструкция нейронной сети для выполнения логических и арифметических операций.

3. Высказывалось предположение, что нейронная сеть способна обучаться, распознавать образы и обобщать полученную информацию.

Фрэнк Разенблатт (1958 г.) ввел понятие перцептрона – модели основного элемента нейронных сетей. Указанный исследователь ввёл возможность модификации межнейронных связей, что сделало нейронную сеть обучаемой. Первые перцептроны могли распознавать буквы алфавита.

Алгоритм обучения перцептрона включает следующие операции:

1) Системе предъявляется эталонный образ;

2) Если результат распознавания совпадает с заданным, то весовые коэффициенты не изменяются;

3) Если нейронная сеть неправильно распознает результат, то весовым коэффициентам дается приращение в сторону повышения качества распознавания.

Однако перцептрон имеет ограниченные возможности, поскольку не всегда существует такая комбинация весовых коэффициентов, при которой заданное множество образов будет распознаваться правильно.

Причина в том, что однослойный перцептрон реализует линейную разделенную поверхность пространства эталона, вследствие чего происходит неверное распознавание, если модель не является сепарабельной.

Сепарабельность – свойство такого пространства, для бесконечного множества элементов которого может быть задан счетный скелет, центр которого обладает центром тяжести и вокруг которого группируются отдельные классы близких по параметрам элементов.

Пространство является нормированным и для него могут быть определены основные свойства нормированного пространства:

- метрика;

- сепарабельность;

- связность;

- конформность.

В метрическом пространстве каждой модели с уникальным набором координат соответствует свой уникальный вектор и единственная точка.

Малое изменение отдельных координат модели приводит к малым изменениям модели и к малым перемещениям точки.

Сепарабельность приводит к тому, что всё множество элементов пространства может быть разделено на отдельные подмножества моделей, похожих по определенным признакам.

Конформность означает, что объем, заданный некоторым множеством моделей в пространстве, может произвольным образом без разрывов деформироваться в целом или своими локальными частями.

Связность предполагает, что множество моделей пространства представляет собой единую унитарную структуру в случае односвязности либо в случае многосвязности, распадается по каким-то признакам на отдельные подмножества.

Для решения проблем предложены модели многослойных перцептронов (рис. 9), которые способны строить ломаную линию.

Многослойные сети

 

В многослойной сети связи устанавливаются только между нейронами соседних слоев. Каждый слой соединен модифицированной связью с любым нейроном соседних слоев. Между нейронами одного слоя связей нет. Каждый нейрон может посылать сигнал только в вышестоящий слой и принимать выходной сигнал только из нижестоящего слоя. Выходные сигналы подаются на нижний слой, а выходной вектор определяется путем последовательных вычислений уравнений активных элементов каждого слоя снизу вверх с использованием уже известных значений активных элементов предшествующих слоев.

Рисунок 9 - Схема многослойного персептрона

 

При распознавании образов входной вектор соответствует наибольшему признаку, а выходной – распознаваемым образам.

Число нейронов в следующем слое в два раза меньше, чем предыдущем.

Простой персептрон формирует границы области решений в виде гиперплоскости. Двухслойный персептрон выполняет множество функций.

 

Рекуррентные сети

Представленные сети (рис. 10) содержат образы связей. Благодаря им становится возможным получать отличные значения при одних и тех же входных данных.

 

Рисунок 10 - Схема рекуррентной сети

 

Особенность способа заключается в представлении появления новых объектов.

Модель Хопфилда

В данной модели также используются правила Хебба. Основана на простом предположении, которое заключается в том, если два нейрона возбуждены вместе, то сила связи возрастает, если порознь, то уменьшается связь. Сеть Хопфилда строится с учетом следующих условий:

1. Все элементы связаны со всеми;

2. Прямые и обратные связи симметричны;

3. Диагональные элементы матрицы связей равны 0, т.е. исключаются обратные связи с выходом на входе одного нейрона.

Сеть Хопфилда может выполнять функции ассоциативной памяти, обеспечивая сходность к тому образу, в область которого попадает начальный образец. Указанный подход привлекателен тем, что нейронная сеть запрограммирована без обучения итераций.

Хопфилд выявил функции энергии нейронной сети. При выявлении выполнено функциональное описание поведения сети через стремление к минимуму энергии, которое соответствует заданному набору образов. Веса связей вычисляются на основе вида функции энергии.

Машина Больцмана развивает теорию Хопфилда. Ее предложили Хинтон и Земел. Используется для решения комбинаторных задач. Указанные сети получили применение в основе реализации подсистем более сложных. Представленные сети также имеют определенные недостатки, которые заключаются в:

1) Предположении о симметричности связи между элементами, без которых нельзя ввести понятие энергии.

2) Нейронная сеть – это устройство для запоминания и обработки информации. Закон энергии играет вспомогательную роль, а не устраивает минимизацию энергии. Сеть Хопфилда поддерживает много лишних связей. В реальности система этого не поддерживает. Происходит освобождение от сильных связей за счет их структуризации. При этом вместо органов связи всех со всеми используется многослойная иерархическая система связи.

 

Самоорганизованные сети Кохонена

Идея сетей с самоорганизацией на основании конкуренции между нейронами базируется на применении специальных алгоритмов самообучения искусственных нейронных сетей.

Сети Кохонена обычно содержат один выходной слой обработки элементов с пороговой передаточной функцией. Число нейронов в выходном слое соответствует комплексному распознаванию классов.

Настройка параметров межнейронных соединений проводится автоматически на основе меры близости векторов – весовых коэффициентов настраиваемых связей к вектору входного сигнала в евклидовом пространстве. В конкурентной борьбе побеждает нейрон со значениями весов наиболее близком к нормализованным векторам входных сигналов. Кроме того, в самоорганизованных сетях возможна классификация входных образцов.

 

 

7. Области применения интеллектуальных систем и технологий

В силу своего предназначения интеллектуальные информационные системы могут применяться практически в любой сфере человеческой деятельности. Примерами областей, где использование данного подхода уже приносит ощутимые результаты, являются [41]:

· Промышленность:

- Управление производством: составление и оптимизация производственной цепочки посредством распределения технологических шагов как между внутренними подразделениями, так и между сторонними подрядчиками.

- Контроль производственных процессов: сбор и анализ текущей информации, коммуникации с агентами, контролирующими другие подсистемы, принятие и реализация оперативных решений.

- Управление воздушным транспортом: моделирование и оптимизация диспетчерской деятельности аэропорта.

· Предпринимательство:

- Управление информацией: поиск источников, сбор, фильтрация и анализ данных, интеллектуальная обработка больших объемов информации.

- Электронная коммерция открывает широкие возможности для использования интеллектуальных агентов как на стороне продавца, так и на стороне покупателя.

- Управление бизнес-процессами: гибкая автоматизация корпоративной организационной деятельности со сложной внутренней логикой и большим количеством участвующих сторон.

· Медицина:

- Мониторинг пациентов: непрерывный сбор, учет и анализ большого количества отслеживаемых характеристик состояния пациентов на протяжении продолжительного промежутка времени.

- Здравоохранение: возможность обследования и диагностирования пациентов с использованием виртуальных специалистов из различных областей медицины.

· Индустрия развлечений:

- Компьютерные игры: возможность достижения качественно новых уровней посредством использования интеллектуальных агентов для различных участвующих сторон.

- Интерактивные приложения (телевидение, театр, кинематограф): агенты могут создавать иллюзию реальности происходящего действия, позволяя пользователю принимать в нем участие.

Приме­ры ИИС в экономике:

· Intelligent Hedger: основанный на знаниях подход в задачах страхования от риска. Фирма: Information System Department, New York University. Проблема огромного количества постоянно растущих альтернатив стра­хования от рисков, быстрое принятие решений менеджерами по рискам в ускоряющемся потоке информации, а также недостаток соответствующей машинной поддержки на ранних стадиях процесса разработки систем страхования от рисков предполагает обширную сферу различных опти­мальных решений для менеджеров по риску. В данной системе разработ­ка страхования от риска сформулирована как многоцелевая оптимизаци­онная задача. Данная задача оптимизации включает несколько сложностей, с которыми существующие технические решения не справляются. Краткие характеристики: система использует объектное представление, охватывающее глубокие знания по управлению риском и облегчает эму­ляцию первичных рассуждений, управляющих риском, полезных для вы­водов и их объяснений.

· Система рассуждений в прогнозировании обмена валют. Фирма. Department of Computer Science City Polytechnic University of Hong Kong Представляет новый подход в прогнозировании обмена валют, основан­ный на аккумуляции и рассуждениях с поддержкой признаков, присутст­вующих для фокусирования на наборе гипотез о движении обменных курсов. Представленный в прогнозирующей системе набор признаков — это заданный набор экономических значений и различные наборы изменяющихся во времени параметров, используемых в модели прогнозиро­вания. Краткие характеристики: математическая основа примененного подхода базируется на теории Демпстера—Шейфера.

· Nereid. Система поддержки принятия решений для оптимизации работы с валютными опционами. Фирма: NTT Data, The Tokai Bank, Science University of Tokyo. Система облегчает дилерскую поддержку для оптимального ответа как один из возможных представленных вариантов; более практична и дает лучшие решения, чем обычные системы принятия решений. Краткие харак­теристики: система разработана с использованием фреймовой системы CLP, которая легко интегрирует финансовую область в приложение ИИ. Предложен смешанный тип оптимизации, сочетающий эвристические знания с тех­никой линейного программирования. Система работает на Sun-станциях.

· PMIDSS: Система поддержки принятия решений при управлении портфелем. Разработчики: Финансовая группа Нью-Йоркского универ­ситета. Решаемые задачи: выбор портфеля ценных бумаг; долгосрочное планирование инвестиций. Краткие характеристики: смешанная система представления знаний, использование разнообразных механизмов выво­да: логика, направленные семантические сети, фреймы, правила.

 

В настоящее время наиболее значительная доля использования интеллектуальных информационных систем приходится на интеллектуальные информационные агенты.

 

8. Структуры ИНС. Нейросетевая модель на базе сети прямого распространения

9. Области применения интеллектуальных систем и технологий

10. Математическое обеспечение подсистем планирования действий мультиагентных систем

11. Системы классификации моделей представления знаний

12. Критерии оптимизации планирования действий

13. Функциональные модели представления знаний

14. Продукционные модели представления знаний

15. Семантические модели представления знаний

Термин семантические сети означает «смысловая».

Семантика – наука, которая устанавливает отношения между символами и объектами, которые они объясняют, т.е. наука, определяющая смысл знаков.

Семантическая сеть – ориентированный граф, вершины которого представляют понятия, а линии (дуги) отображают отношения между ними (пример на рис.1).

Понятиями обычно выступают абстрактные или конкретные объекты. Отношения – это связи между этими объектами.

Существует несколько классификаций семантических сетей:

1) По количеству отношений различаются:

1. Однородные семантические сети с единственным типом отношений;

2. Неоднородные семантические сети с различными типами отношений.

2) По типам отношений выделяются:

1. Бинарные семантические сети, в которых отношения связывают два объекта;

2. Парные семантические сети, в которых отношения связывают более чем два понятия.

Наиболее часто используются в семантических сетях:

1. Связь «часть – целое» (класс – подкласс, элемент – множество);

2. Функциональные связи (производит, владеет);

3. Количественные отношения (A > 0, B < 0);

4. Пространственные отношения (далеко от, близко от, над, за и т.п.);

5. Временные (раньше, позже, одновременно);

6. Атрибутивные (иметь свойство, иметь значение);

7. Логические связи – «И», «ИЛИ», «НЕ».

Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети согласно поставленному вопросу.

 

Рисунок 1 – Модель в виде семантической сети

 

Преимущества модели:

- совпадает с тем, как человек познает мир;

- соответствует долговременной памяти человека.

Недостатки:

- сложность с поиском вывода.

Реализации: NET, PROSPECTOR, CASNET, TORUS – языки представления знаний в виде семантической сети.

 

16. Алгоритмы локального поиска и задачи оптимизации

17. Фреймовые модели представления знаний

Frame в переводе означает рамка.

Frame в области искусственного интеллекта трактуется как структура знаний для восприятия пространственных сцен.

Под фреймом понимается абстрактный образ или ситуация.

Пример абстрактного образа: слово «комната» – ассоциируется с образом жилого помещения с окнами, дверьми, полом и потолком и с площадью равной примерно 6-20 кв. метров. Есть пустые места – количество окон, цвет стен, высота потолка и т.д.

Типичная структура фрейма имеет вид, рассмотренный на рис. 2.

Рисунок 2 – Структура фрейма

 

Слотом может являться другой фрейм.

Различают фреймы – образцы или прототипы, которые хранятся в базе данных, и фреймы – экземпляры, которые создаются для отражения реальной ситуации на основе поступающих данных.

Пример:

Магазин – образец;

Булочный магазин – экземпляр.

Модель фреймов является действительно универсальной, т.к. позволяет отображать все множество знаний о мире через следующие фреймы:

1. Фрейм-структура – предмет или понятие;

2. Фрейм-роль;

3. Фрейм-сценарий;

4. Фрейм-ситуация.

Важнейшим свойством теории фреймов является заимствование из теории семантических сетей полезных свойств. Реальные фреймовые модели являются сетевыми.

На рис. 3 изображается сеть фреймов, где AKO – это связи (a kind of – это).

Слот АКО указывает на фрейм более высокого уровня иерархии, откуда наследуется свойство.

В школе

Ребенок

АКО Учится Возр

7 – 17 лет

Сладкое

50 - 180см

0-16 лет

Человек

АКО Возраст Рост Люб.

АКО Умеет

Мыслить

Млекопитающее

Человек Ребенок Учится

 

 

Рисунок 3 – Сеть фреймов

 

Основным преимуществом фреймов как модели представления знаний является способность отражать концептуальную основу организации памяти человека, а также гибкость и наглядность.

Существует специальный язык представления знаний в сетях фреймов – FRL, на нем построены промышленные экспертные системы ANALIST, НОДИС.

 

18. Информационный поиск. Семантизация процесса поиска

19. Модели теорий логик в представлении знаний

20. Лексические синонимы в лингвистике и системах поиска

21. Модели теории нечётких множеств в представлении знаний

22. Сравнительный анализ систем информационного поиска

23. Модели теории нейронных сетей в представлении знаний

24. Нотации моделей представления знаний

2. Функциональные классы экспертных систем

25. Онтологические модели в представлении знаний

26. Инструментальные системы построения моделей представления знаний

27. Интерпретирующие экспертные системы

28. Пропозициональная логика. Шаблоны формирования рассуждений в пропозициональной логике

29. Экспертные системы прогнозирования

30. Агенты на пропозициональной логике

31. Экспертные системы мониторинга

32. Логика первого порядка. Инженерия знаний с логикой первого порядка

33. Экспертные системы ремонта. Системы интеллектуального обучения

34. Многослойные нейронные сети. Формальные правила выбора размера скрытых слоёв

35. Унифицированные системообразующие компоненты экспертных систем

36. Определение структур нейронных сетей в процессе обучения

37. Процедуры обработки знаний в экспертных системах

38. Применения нейросетевых подходов в технических приложениях

39. Инструментальные среды создания экспертных систем

40. Генетические алгоритмы нейросетевых подходов

41. Архитектура интеллектуальных систем обучения

42. Области применения мультиагентных систем

43. Виды онтологий. Операции над онтологиями

Онтология – система, состоящая из набора понятий, на основе которых строятся отношения, функции, классы, объекты и теории предметной области. Онтология описывается следующим кортежем:

 

O = < A, B, C >,

 

где А – конечное множество понятий, терминов (концепций) предметной области, которые представляют данную онтологию.

В – конечное множество отношений между концепциями (понятиями) данной предметной области.

С – конечное множество функций интерпретации, заданной на A и B.

Онтологии рассматриваются как базы знаний специального типа, которые могут читаться, пониматься, физически разделяться или отчуждаться от разработчиков. По мере развития инженерии знаний выделяется отдельная ветвь профессиональной деятельности, именуемая онтологически инжинирингом.

 

44. Модельно-аналитический интеллект для сравнения эффективности систем управления взаимоотношениями с клиентами на основе теории нечётких множеств

45. Методология формирования модельно-аналитического интеллекта для контроля действий информационных систем

46. Методология формирования модельно-аналитического интеллекта информационных систем

47. Алгоритм SNLP планирования действий интеллектуальных информационных агентов

Алгоритм SNLP для нахождения плана Р при заданном множестве целевых предусловий А можно представить на основе обобщенного алгоритма Refine-Plan. Схема алгоритма SNLP приведена на рис.1.1 и 1.2. Алгоритм SNLP вызывает следующие функции и процедуры:

Функция SNLP_Sol(P,G):

Если множество А пусто, возвратить решение. Если множество А не пусто и длина плана не превысила 1_т, возвратить значение «продолжить». Если множество А не пусто и длина плана превысила l_m, возвратить значение «нет решений».

Процедура SNLP_pick-prec:

Произвольным образом выбрать из множества целевых предусловий А цель <с,t> (где с – предусловие оператора, соответствующего шагу t). Убрать цель <с,t> из множества целевых предусловий А (А = А - < с,t >).

Процедура SNLP_establish:

Выбрать существующий или новый шаг t’ для < с,t >, устанавливающий условие с перед шагом t (если шаг t’ не существует и не может быть добавлен, вернуться в предыдущую точку возврата). (1) Дополнить множество шагов Т шагом t . Дополнить множество упорядочивающих ограничений О ограничением , гарантирующим выполнение шага t’ перед шагом t . (2) Дополнить множество ограничений инициализаций переменных В множеством В’, состоящим из совместных и несовместных инициализаций, содержащихся во множестве precond(t’) – множестве предусловий выполнения шага t’ 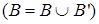. (3) Для каждого шага t'', выполняемого между t’ и t и нарушающего условие c, выполнить два уточнения плана: первое – с помощью ограничения , и второе – с помощью ограничения Если шаг t' ранее не встречался в плане, то дополнить множество целевых предусловий А и множество дополнительных ограничений L:

;

.

Процедура SNLP_save:

Добавить вспомогательные ограничения, гарантирующие сохранность сделанного уточнения плана с использованием стратегии защиты с помощью уточнений (contributor protection strategy), которая обеспечивает систематичность поиска):

.

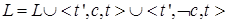Процедура SNLP_tract:

Используется способ 2.b, позволяющий разрешать конфликты. (1) Определить конфликты. Шаг t_conf считается конфликтующим с IPC-ограничением , если ,причем шаг t_conf может быть выполнен между шагами t₁ и t₂, и выполнение t_conf нарушит условие р.

(2) Разрешить конфликты. Для каждого конфликта, состоящего из шага t_conf и IРС-ограничения , произвести два уточнения плана, первое – с помощью ограничения 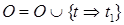, а второе – с помощью ограничения .

Функция SNLP_check:

Если план нецелостный, возвратить значение «нецелостный план», иначе – возвратить значение «целостный план». Нарушением целостности плана является 1) наличие циклов в порядке следования операторов (проверка множества упорядочивающих ограничений О на наличие замкнутых цепочек вида: или 2) наличие для пары переменных одновременно совместной и несовместной инициализации (проверка множества ограничений инициализаций переменных В).

рис.1.1

рис.1.2

48. Формирование модельно-аналитического интеллекта информационных агентов для преодоления априорной неопределённости относительно инфраструктуры при последовательной обработке запросов к информационным ресурсам

49. Алгоритм NONLIN планирования действий интеллектуальных информационных агентов

Алгоритм SNLP является развитием семейства алгоритмов NONLIN. Принципиальным различием между NONLIN и SNLP является использование ими различных стратегий при регистрации уточнений (шаг 1.3). В NONLIN используется стратегия защиты интервала (interval preservation strategy). Следует заметить, что используемая в NONLIN стратегия может приводить к более быстрому нахождению решений для некоторых задач, так как стратегия проверки целостности SNLP может приводить к более частым возвратам. Но для других задач поиск с помощью NONLIN может быть более долгим и избыточным (используемая стратегия не гарантирует систематичности поиска). Для анализа отличий алгоритмов при решении задач планирования используется McNONLIN – разновидность алгоритма NONLIN, описание которого на основе обобщенного алгоритма Refine-Plan полностью идентично описанию алгоритма SNLP за исключением шага 1.3. При регистрации уточнений на шаге 1.3. вместо процедуры SNLP_save вызывается процедура NONLIN_save.

Процедура NONLIN_save:

Добавить вспомогательные ограничения, гарантирующие сохранность сделанного уточнения плана с использованием стратегии защиты с помощью уточнений (contributor protection strategy), которая не обеспечивает систематичность поиска:

.

50. Формирование модельно-аналитического интеллекта информационных агентов для преодоления априорной неопределённости относительно инфраструктуры при масштабируемой обработке запросов к информационным ресурсам

51. Алгоритм TWEAK планирования действий интеллектуальных информационных агентов

Основное отличие TWEAK от SNLP и NONLIN заключается в том, что TWEAK не использует ограничения для регистрации уточнений плана. Таким образом, TWEAK не задействует ни шаг 1.З., ни шаг 2 обобщенного алгоритма. Кроме того, TWEAK использует МТС-критерий для оценки того, что является ли целевое предусловие необходимо истинным (то есть справедливо для всех элементарных линеаризаций плана). При выборе цели (шаг 1.1.) предпочитаются целевые предусловия, для которых не выполняется МТС-критерий. Проверка наличия решения (шаг 0.) завершается успешно в том случае, если МТС-критерий выполняется для всех целевых предусловий из множества А. Схема алгоритма TWEAK на основе обобщенного алгоритма Refine-Plan [39] приведена на рис. 3.1 и 3.2. Далее приводятся описания процедур и функций, вызываемых алгоритмом TWEAK и отличных от процедур и функций, приведенных в первом случае.

Функция TWEAK_Sol(P,G):

Если каждая цель (где с – предусловие оператора, соответствующего шагу t) из множества целевых предусловий А необходимо истинна согласно МТС-критерию, то возвратить решение. Если нет и длина плана не превысила l_т, то возвратить значение «продолжить». Если нет и длина плана превысила l_т, то возвратить значение «нет решений».

Процедура TWEAK_pick-prec:

Произвольным образом выбрать из множества целевых предусловий A цель 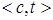, для которой не выполняется МТС-критерий. Не удалять цель 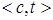из А.

Из описания следует, что TWEAK не исключает рассматриваемые цели из множества целевых предусловий А и поэтому теоретически может рассмотреть одно и то же целевое предусловие более одного раза. Кроме того, хотя TWEAK не уменьшает вычислительную сложность (не задействует шаг 2), за счет использования МТС-критерия алгоритм сохраняет свойство полноты.

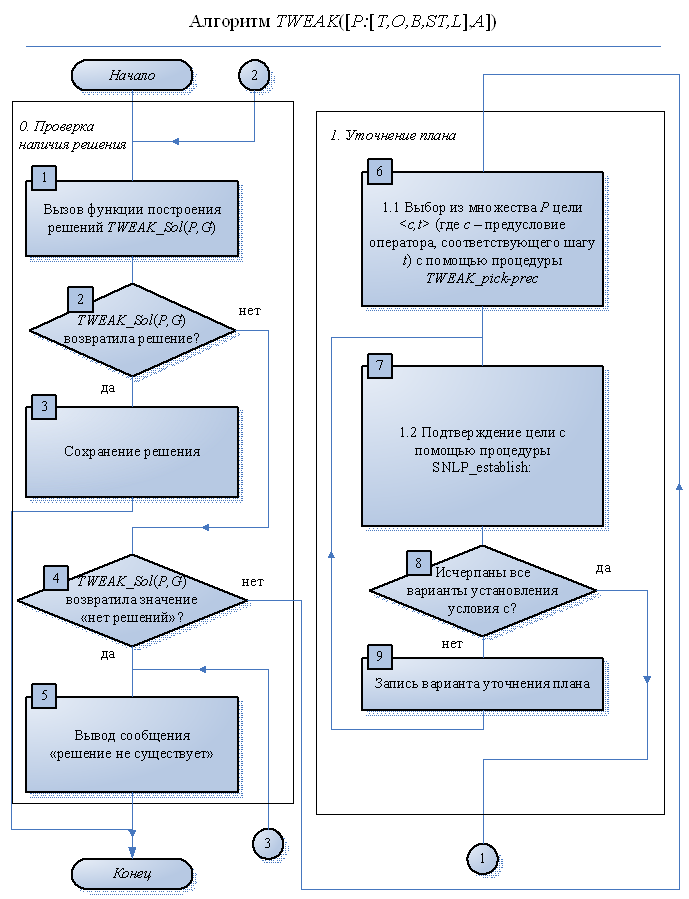рис.3.1

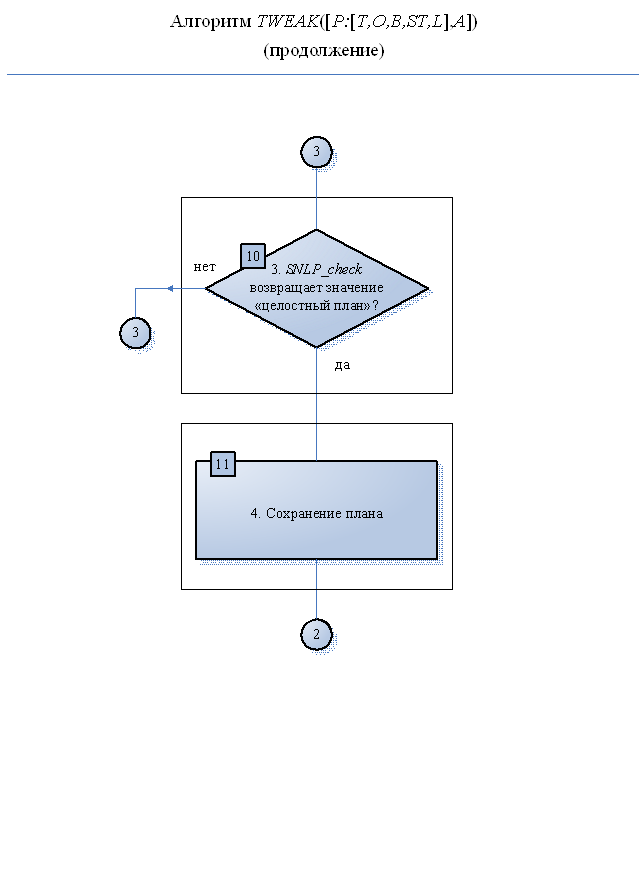
рис.3.2

 

52. Формирование модельно-аналитического интеллекта информационных агентов для обеспечения гарантий достижимости целей при последовательной обработке запросов к информационным ресурсам

53. Алгоритм UA планирования действий интеллектуальных информационных агентов

UA во многом аналогичен алгоритму TWEAK, Он также не регистрирует уточнения плана и использует аналогичные стратегии выбора цели и проверки наличия решения. Принципиальным отличием между UA и TWEAK является только наличие в UA шага уменьшения вычислительной сложности (шаг 2.), на котором в UA используется предварительное упорядочивание (шаг 2.а. обобщенного алгоритма). Таким образом, для описания UA на основе обобщенного алгоритма достаточно взять за основу описание алгоритма TWEAK, приведенное в Приложении 3, и заменить процедуру, вызываемую на шаге 2 для уменьшения вычислительной сложности, на процедуру UA_tract.

Процедура UA_tract:

Используется способ 2.а. – предварительное упорядочивание. (1) Определение пересечений. Пара шагов плана t₁ и t₂ считаются пересекающимися, если они не упорядочены относительно друг друга (множество О не содержит ни упорядочивающего ограничения , ни упорядочивающего ограничения 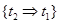и выполняется одно из следующих трех условий:

(I) t₁ содержит предусловие p, а t₂ содержит постусловие p или p;

(II) t₂ содержит предусловие p, a t₁ содержит постусловие p или p;

(III) t₁ содержит постусловие p, а t₂ содержит постусловие p.

На шаге 2.а. (1) требуется найти все шаги t ', пересекающиеся с шагом t.

(2) Разрешение пересечений. Для каждого шага t ', пересекающегося с шагом t, требуется добавить либо упорядочивающее ограничение , либо упорядочивающее ограничение . Для гарантирования полноты поиска необходимо рассмотреть оба варианта.

Из описания стратегии UA на шаге 2. следует, что все частично-упорядоченные планы, генерируемые UA, являются однозначными (unambiguous), то есть каждое целевое предусловие 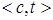либо необходимо истинно (то есть справедливо для всех элементарных линеаризаций плана), либо необходимо ложно (то есть не выполняется для всех элементарных линеаризаций плана). В связи с этим для проверки МТС-критерия в UA достаточно исследовать только одну элементарную линеаризацию плана.

 

54. Формирование модельно-аналитического интеллекта информационных агентов для обеспечения гарантий достижимости целей при масштабируемой обработке запросов к информационным ресурсам

55. Концепция системы выбора оптимального алгоритма планирования действий интеллектуальных информационных агентов

56. Параметризация предметной области при определении свойств окружающей среды для интеллектуальной информационной системы

57. Универсальные показатели качества интеллектуальных информационных агентов

58. Экспертная система выбора оптимального алгоритма планирования действий интеллектуальных информационных агентов

59. Формализация отбора доступной информации при оптимизации планирования действий интеллектуальных информационных агентов

60. Специфические показатели качества интеллектуальных информационных агентов

61. Структурное описание алгоритмов планирования действий интеллектуальных информационных агентов

62. Проектирование интеллектуальных информационных систем в условиях рыночной экономики